Евклидтыҡы булмаған геометрия
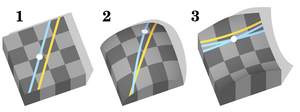
Евклидтыҡы булмаған геометрия — һүҙмә-һүҙ аңлағанда — Евклид геометрияһынан айырылған һәр төрлө геометрик система; әммә традицион рәүештә «Евклидтыҡы булмаған геометрия» термины тағы ла тарыраҡ мәғәнәлә ҡулланыла һәм тик традицион Евклидтыҡы булмаған геометрик системаларға ҡарай: Лобачевский геометрияһы һәм сфера геометрияһы (йәғни уға оҡшаған Риман геометрияһы).
Евклид геометрияһы һымаҡ был геометриялар даими кәкрелек киңлегенең метрик геометрияларына ҡарай. Ноль кәкрелеге Евклид геометрияһына тап килә, ыңғай кәкрелек — локаль үҙенсәлектәре буйынса сфера йәки Риман геометрияһына тура килә, тиҫкәре кәкрелек — Лобачевский геометрияһы.
Яҫылыҡ өсөн метрика
[үҙгәртергә | сығанаҡты үҙгәртеү]Бер төрлө планиметриялар өсөн метриканың төрө һайланған (кәкре һыҙыҡлы) координаталар системаһына буйһона; артабан ярым геодезик координаталар өсөн формулалар килтерелә:
- Евклид геометрияһы: (Пифагор теоремаһы).
- Сфера геометрияһы: . Бында R — сфеараның радиусы.
- Лобачевский геометрияһы: . Бында R — Лобачевский яҫылығы кәкрелегенең радиусы, ch — гиперболик косинус.
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]- Александров А. Д., Нецветаев Н. Ю. Геометрия. — Наука, Москва, 1990. ISBN 978-5-9775-0419-5.
- Александров П. С. Что такое неэвклидова геометрия. — УРСС, Москва, 2007. ISBN 978-5-484-00871-1.
- Алексеевский Д. В., Винберг Э. Б., Солодовников А. С. Геометрия пространств постоянной кривизны. — Итоги науки и техники. Серия: Современные проблемы математики. Фундаментальные направления. 1988, том 29, стр. 5-146.
- Берже М. Геометрия. Пер. с франц., в двух томах. М., «Мир», 1984. 928 с. Том II, часть V: Внутренняя геометрия сферы, гиперболическая геометрия.
- История математики с древнейших времён до начала XIX столетия (под ред. А. П. Юшкевича), тома I—III, М., Наука, 1972.
- Делоне Б. Н. Элементарное доказательство непротиворечивости планиметрии Лобачевского, — Гостехиздат, Москва, 1956.
- Клейн Ф. Неевклидова геометрия. М.: изд. НКТП СССР, 1936, 355 с.
- Лаптев Б. Л. Н. И. Лобачевский и его геометрия. М.: Просвещение, 1976.
- Мищенко А. С., Фоменко А. Т. Курс дифференциальной геометрии и топологии, — Факториал, Москва, 2000.
- Прасолов В. В. Геометрия Лобачевского. Изд. 3-е, МЦНМО, 2004. ISBN 5-94057-166-2.
- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.



