Квадрат тамыр

-нан Квадра́т тамыр (2-се дәрәжә тамыр, ) — ул тигеҙләмәһенең сығарылышы. Икенсе төрлө әйткәндә, һанының квадрат тамыры — квадратҡа күтәргәндә һанын биреүсе һан ул. ҡиммәтен табыу ғәмәле һанынан «квадрат тамыр алыу» тип атала. Йышыраҡ һәм аҫтында һан күҙ уңында тотола, ләкин ҡайһы бер ҡушымталарҙа улар башҡа математик объекттар булырға мөмкин, мәҫәлән матрица һәм операторҙар. Ысын һандар өсөн миҫал: , сөнки Квадрат тамырҙың ҡапма-ҡаршы, йәғни тамғаһы менән айырылып торған ҡиммәттәре бар (был миҫалда, ыңғай һәм тиҫкәре һандар), һәм был тамырҙар менән эште ҡатмарлаштыра. Бер мәғәнәлелекте тәьмин итер өсөн, арифметик тамыр төшөнсәһе индерелә, тиҫкәре булмаған өсөн ҡиммәте һәр ваҡыт тиҫкәре түгел (ә ыңғай өсөн — ыңғай; миҫалда был һан 3).
Тамыр алыу ғәмәлен һандарға ҡулланыу
[үҙгәртергә | сығанаҡты үҙгәртеү]һанынан квадрат тамыр — ул квадраты (үҙенә ҡабатлау һөҙөмтәһе) -ға тигеҙ булған һан, йәғни тигеҙләмәһенең үҙгәреүсәненә ҡарата сығарылышы.[комм. 1][комм. 2]
Рациональ һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]рациональ һан булғанда тигеҙләмәһенең һәр ваҡытта ла рациональ сығарылышы булмай. Улай ғына түгел, бындай тигеҙләмәнең, хатта ыңғай булғанда ла, ҡыҫҡармай торған кәсер рәүешендә күрһәтелгән һанының числителе һәм знаменателе квадрат һандар булғанда ғына һәм тик шул саҡта ғына рациональ һандар күмәклегендә сығарылышы бар.
Рациональ һандан тамырҙың өҙлөкһөҙ кәсере һәр саҡ периодлы. Был бер яҡтан уға яҡшы рациональ яҡынлауҙы һыҙыҡлы рекуррент ярҙамында еңел иҫәпләргә мөмкинлек бирә, ә икенсе яҡтан яҡынлауҙың теүәллеген сикләй: , бында -ға бәйле[1][2]. Шул да дөрөҫ, теләһә ниндәй периодлы сынйырлы кәсер квадрат иррационалле була.
Ысын һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]Теорема. Теләһә ниндәй ыңғай һаны өсөн модулдәре буйынса тигеҙ, тамғалары ҡапма-ҡаршы булған теүәл ике ысын тамыр бар.[3] Тиҫкәре булмаған һанынан тиҫкәре булмаған квадрат тамыр арифметик квадрат тамыр тип атала һәм радикал тамғаһы ҡулланып тамғалана [4].
Комплекслы һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]Комплекслы һандар яланы өҫтөндә тамғаһы менән генә айырылып торған сығарылышы һәр саҡ икәү (нулдән квадрат тамырҙан башҡа). комплекслы һанынан тамырҙы йыш ҡына тип тамғалайҙар, ләкин был тамғалауҙы һаҡ ҡулланырға кәрәк. Киң таралған хата:
Комплекслы һандан квадрат тамыр алыу өсөн комплекслы һандың яҙылышының экспоненциаль формаһын ҡулланыу уңайлы: әгәр
- , ул саҡта (Муавр Формулаһын ҡара)
- ,
бында модулдән тамырҙы арифметик ҡиммәте мәғәнәһендә аңлайбыҙ, ә k k = 0 һәм k = 1 ҡиммәттәре ҡабул итергә мөмкин, шулай итеп яуапта төрлө ике һөҙөмтә табабыҙ.
Квадрат тамыр элементар функция булараҡ
[үҙгәртергә | сығанаҡты үҙгәртеү]
Квадрат тамыр элементар функция һәм дәрәжәле функцияның булғандағы айырым осрағы булып тора. Арифметик квадрат тамыр булғанда шыма функция була, нуль нөктәһендә уңдан шыма, ләкин дифференцияланмай.[5]
Комплекслы үҙгәреүсән функцияһы булараҡ тамыр — ике ҡиммәтле функция, биттәре нуль нөктәһендә ҡушылалар.
Дөйөмләштереү
[үҙгәртергә | сығанаҡты үҙгәртеү]Квадрат тамыр башҡа объекттар өсөн күренешендәге тигеҙләмәләрҙең сығарылышы рәүешендә индерелә: матрицалар[6], функциялар[7], операторҙар (математика)[8] һ.б. Шуның менән бергә ғәмәле сифатында ирекле мультипликатив ғәмәлдәр, мәҫәлән, функциялар композицияһы (суперпозиция) ҡулланылырға мөмкин. Алгебрала түбәндәге формаль билдәләмә ҡулланыла: — группоид булһын һәм . Әгәр булһа, элементы -нан квадрат тамыр тип атала.
Элементар геометрияла квадрат тамыр
[үҙгәртергә | сығанаҡты үҙгәртеү]Квадрат тамырҙар элементар геометрия менән тығыҙ бәйләнгән: әгәр 1 оҙонлоғондағы киҫек бирелһә, ул саҡта циркуль һәм линейка ярҙамында оҙонлоғо бөтөн һандар, дүрт арифметик ғәмәл тамғаһы, квадрат тамыр тамғаһы ингән аңлатма менән күрһәтелгән киҫектәрҙе һәм тик шундай киҫектәрҙе генә төҙөргә мөмкин. [9]
Информатикала квадрат тамыр
[үҙгәртергә | сығанаҡты үҙгәртеү]Функциональ кимәлдәге күп программалау телдәрендә (шулай уҡ LaTeX тибындағы билдәләү телдәрендә) квадрат тамыр функцияһы sqrt тип тамғалана(ингл. square root «квадрат тамыр» һүҙенән).
Квадрат тамыр табыу алгоритмы
[үҙгәртергә | сығанаҡты үҙгәртеү]Бирелгән һандан квадрат тамырҙы табыу йәки иҫәпләү (квадрат) тамыр алыу тип атала.
Тейлор рәтенә тарҡатыу
[үҙгәртергә | сығанаҡты үҙгәртеү]- при .
Тупаҫ баһа
[үҙгәртергә | сығанаҡты үҙгәртеү]Күп ыңғай ысын һандан квадрат тамыр алыу алгоритмдары S ниндәй ҙә булһа башланғыс ҡиммәт булыуын талап итә. Әгәр башланғыс ҡиммәт тамырҙың ысын ҡиммәтенән ныҡ алыҫ булһа, иҫәпләү әкренәйә. Шуға күрә бик теүәл булмаһа ла, еңел иҫәпләнгән тупаҫ баһаны белеү файҙалы. Әгәр S ≥ 1 булһа, D - Sҡиммәтенең унарлы өтөрҙән һул яҡтағы цифрҙар һаны булһын, ти. Әгәр S < 1 булһа, D - минус тамғаһы менән алынған унарлы өтөрҙән уң яҡта рәттән килеүсе нулдәр һаны булһын. Ул саҡта тупаҫ хата түбәндәге күренештә:
- Әгәр D таҡ булһа, D = 2n + 1, ул саҡта ҡулланабыҙ.
- Әгәр D йоп булһа, D = 2n + 2, ул саҡта ҡулланабыҙ.
Ике һәм алты ҡулланыла, сөнки и Икеле иҫәпләү системаһында эшләгәндә (компьютер эсендәге кеүек), икенсе баһаны ҡулланырға кәрәк: (бында D икеле цифрҙар һаны).
Геометрик юл менән квадрат тамыр алыу
[үҙгәртергә | сығанаҡты үҙгәртеү]
Итерацион аналитик алгоритм
[үҙгәртергә | сығанаҡты үҙгәртеү]Основная статья: Герон итерацион формулаһы ул саҡта
Бағаналап
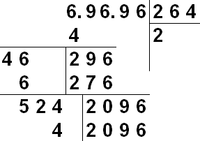
[үҙгәртергә | сығанаҡты үҙгәртеү]Был ысул теләһә ниндәй ысын һандан теләһә ниндәй алдан бирелгән аныҡлыҡ менән тамырҙың яҡынса ҡиммәтен табырға мөмкинлек бирә. Ысулдың етешһеҙлегенә табылған цифрҙар һаны күбәйгән һайын иҫәпләүҙең ҡатмарлылығы арта барыуын индерергә була. Ҡулдан тамыр алыу өсөн бағаналап бүлеүгә оҡшаған яҙыу ҡулланыла. Тамырын табырға кәрәк булған һан күсереп яҙыла. Унан уң яҡта эҙләнгән тамырҙың цифрҙарын әкренләп таба башлайбыҙ. Өтөрҙән һуң сикле һандағы тамғалары булған N һанынан квадрат тамыр алырға кәрәк булһын, ти. Иң тәүҙә уйҙа ғына йәки билдә ярҙамында N һанын унарлы нөктәнән уңда һәм һулда икешәр цифрҙан торған төркөмдәргә бүлеп сығабыҙ. Кәрәк булғанда, төркөмдәр нулдәр менән тулыландырылалар - бөтөн өлөшө һулдан, ә кәсер өлөшө уңдан тулыландырыла. Шулай, 31234,567 һанын 03 12 34, 56 70 күренешендә яҙырға кәрәк. Бүлеүҙән айырмалы рәүештә, цифрҙар икешәрләп төркөмдәре менән төшөрөләләр.
- Дәфтәр битенә N һанын яҙырға (миҫалда — 69696).
- Квадраты N һанының өлкән разряды төркөмөнә тигеҙ йәки кәмерәк булған һанын табырға (өлкән төркөм — нулгә тигеҙ булмаған иң һулдағы төркөм), ә -ҙең квадраты һандың өлкән разряд төркөмөнән ҙур. Табылған һанын N-дан уң яҡта яҙып ҡуябыҙ (был эҙләнгән тамырҙың сираттағы цифры). (Миҫалдың беренсе аҙымында math>a^2=2^2=2 \cdot 2=4 < 6</math>, ә ).
- һанының квадратын өлкән разряд төркөмө аҫтына яҙабыҙ. N һанының өлкән разряд төркөмөнән аҫтында яҙылған һанының квадратын алабыҙ һәм һөҙөмтәне улар аҫтына яҙабыҙ.
- Был алыу һөҙөмтәһенең һул яғынан вертикаль һыҙыҡ үткәрәбеҙ һәм һыҙыҡтан һулда һөҙөмтәнең табылған цифрҙарының (беҙ уларҙы N һанынан уң яҡта яҙып ҡуябыҙ) 20-гә ҡабатландығына тигеҙ булған һанды яҙабыҙ. Был һанды тип атайыҡ. (Миҫалдың беренсе аҙымында был һан , икенсеһендә ).
- Артабанғы төркөм цифрҙарҙы төшөрөп яҙабыҙ, йәғни алыу һөҙөмтәһенә уң яҡтан N һанының артабанғы ике цифрын өҫтәп яҙабыҙ. Алыу һөҙөмтәһе менән сираттағы ике цифр төркөмөн берләштереүҙән килеп сыҡҡан һанды һаны тип атайыҡ. (Миҫалда беренсе аҙымда был һан , икенсеһендә ). Әгәр беренсе төркөм N һанының унарлы өтөрөнән һуң төшһә, эҙләнгән тамырҙың табылған цифрҙарынан һуң уң яҡта нөктә ҡуйырға кәрәк.
- Хәҙер шундай һанын табырға кәрәк, -нан бәләкәй йәки тигеҙ, ләкин һанынан ҙурыраҡ булһын. Табылған һанын N-дан уң яҡта, эҙләнгән тамырҙың сираттағы цифры итеп яҙырға. Ихтимал, һаны нуль булырға мөмкин. Был бер нәмәне лә үҙгәртмәй — 0-де тамырҙың табылған цифрҙарынан уң яҡта яҙабыҙ. (миҫалда беренсе аҙымда был һан 6, сөнки , ләкин ) Әгәр табылған цифрҙар бирелгән аныҡлыҡты ҡәнәғәтләндерһә, иҫәпләү процессын тамамлайбыҙ.
- һанын һаны аҫтына яҙабыҙ. Бағаналап һанын һанынан алабыҙ һәм алыу һөҙөмтәһен улар аҫтына яҙабыҙ. 4-се аҙымға күсәбеҙ.
Алгоритмдың күргәҙмә һүрәтләмәһе:
Шулай уҡ ҡарағыҙ
[үҙгәртергә | сығанаҡты үҙгәртеү]- Тиҙ инверслы квадрат тамыр
- Вложенные радикалы
- Квадрат тамыр көнө
- Герондың итерацион формулаһы
- Квадрат тигеҙләмә
- Тамыр (математика)
- Куб тамыр
- Абель — Руффини теоремаһы
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ x һанының n-се дәрәжә тамыры тип n-се дәрәжәһе x-ҡа тигеҙ булған һан атала. n = 2 һәм n = 3 булғанда тамырҙар ярашлы рәүештә квадрат һәм куб тамырҙар тип аталалар.
— Алгебра // Энциклопедия «Кругосвет».
- ↑ а һанынан n-се дәрәжә тамыр алыу— ул n-се дәрәжәгә күтәргәндә бирелгән а һанын биреүсе x һанын табыу тигән һүҙ ()… 2-се дәрәжә тамыр квадрат тамыр тип атала.
— [ Извлечение корня] — Ҙур совет энциклопедияһында мәҡәлә
- ↑ алгебраик һандарҙың яҡынлауы тураһында Лиувилль теоремаһы
- ↑ См. А. Я. Хинчин, Цепные дроби 2021 йыл 2 ноябрь архивланған., М. ГИФМЛ, 1960, §§ 4, 10.
- ↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
- ↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
- ↑ Фихтенгольц, гл. 2, § 1
- ↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148





























![{\displaystyle {\sqrt {\sqrt {1\cdot 10}}}={\sqrt[{4}]{10}}\approx 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2eeb6a3f3bd5de4533a82fdb3dfd8d86223ffc1)
![{\displaystyle {\sqrt {\sqrt {10\cdot 100}}}={\sqrt[{4}]{1000}}\approx 6\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b0b8d8cc44d57a544d6398144d88707458ffa0)