Картографик проекциялар

Картографик проекциялар
	Картографик проекциялар
Вики-проект	Проект:Математика[d]
	Картографик проекциялар Викимилектә

Картографик проекция— Ерҙең^[1] (йә башҡа күк есемдәре, йәки дөйөм мәғәнәлә, теләһә ниндәй бөгөлгән өҫкө йөҙө булған есемдең) өҫкө йөҙөн яҫылыҡҡа сағылдырыуҙың математик билдәләнгән ысулы, йәғни ҡағыҙҙа һүрәтләнеше.

Проекцияларҙың асылы күк есемдәре фигураһын яҫылыҡҡа йәйеп һалып рәсемен төшөрөү.^[2] Шул уҡ ваҡытта эллипсоидтан икенсе фигураға параллелдәр һәм меридиандар селтәрен күсереү. Был селтәр күп төрлө була, эллипсоидтың ниндәй фигура менән алмашыныуына бәйле була.

Теге йәки был картографик проекцияларҙың ҡулланылыуы картаның тәғәйенләнеүенә, конфигурацияһына һәм картографияланған өлкәнең торошона бәйле.^[2]

Проекцияла бөҙолоуҙар

Теләһә ниндәй проекцияла ла боҙоп күрһәтеүҙәр бар, улар дүрт төрҙә була:

оҙонлоғо боҙолоу
мөйөшө боҙолоу
майҙаны боҙолоу
формаһы боҙолоу

Төрлө карталарҙа боҙолоуҙар төрлө ҙурлыҡта булырға мөмкин: эре масштаблы карталарҙа улар һиҙелмәй тиерлек, әммә ваҡ масштаблы картала улар бик ҙур була.

Оҙонлоғо боҙоулоу

Оҙонлоғо боҙолоуы - логик яҡтан башҡа боҙолоуҙар килеп сыҡҡан төп боҙолоу. Бының сәбәбе булып эллипсоидтың (йәки шарҙың) өҫкө йөҙөн йыйырсыҡтарһыҙ йәки өҙөлөктәрһеҙ яҫылыҡта әйләндереү мөмкин түгел.^[2] Оҙонлоҡтарҙың боҙолоуы яҫы һүрәттең масштабының тотороҡһоҙлоғон аңлата, был масштабтың нөктәһенән нөктәгә, хатта бер үк нөктәлә, йүнәлешкә ҡарап, үҙгәреүендә сағыла.

Тимәк, картала масштабтың 2 төрө бар:

Төп масштаб, ул картала яҙыла, әммә ысынында был эллипсоидтың башланғыс масштабы, уны карта яҫылығына йәйелдереп алып, алына.
Осраҡлы масштаб картала сикһеҙ күп, ул нөктәләрҙән нөктәгә үҙгәрә, хатта бер нөктәлә лә төрлө йүнәлештәрҙә төрлө булыуы мөмкин.

Осраҡлы масштабты күрһәтеү өсөн боҙолоуҙар эллипсын төҙөйҙәр.

Майҙан боҙолоуы

Майҙан боҙолоуы логик яҡтан оҙонлоҡтарҙың боҙолоуынан килеп сыға. Майҙандарҙың боҙолоуын тасуирлау өсөн эллипс майҙанының эллипсоидтағы башланғыс майҙандан тайпылыуын ҡабул итәләр.

Мөйөштәрҙең боҙолоуы

Мөйөштәрҙең боҙолоуы логик яҡтан оҙонлоҡтарҙың боҙолоуынан килеп сыға. Картала мөйөштәрҙең боҙолоуын һүрәтләү өсөн карталағы йүнәлештәр һәм эллипсоид өҫтөндәге йүнәлештәр араһындағы мөйөштөң айырмаһын ҡабул итәләр.

Форма боҙолоу

Форманың боҙолоуы — эллипсоидтың яҫылыҡта график һүрәтләмәһе.

Проекцияларҙы боҙолоу характеры буйынса классификациялау

Тигеҙ мөйөшлө проекциялар

Тигеҙ мөйөшлө проекциялар — мөйөштәрҙе боҙолмаған проекциялар. Навигация мәсьәләләрен хәл итеү өсөн бик уңайлы. Масштаб нөктәнең торошона ғына бәйле һәм йүнәлешенә бәйле түгел. Ерҙәге мөйөш һәр ваҡыт карталағы мөйөшкә тиң, урындағы линия картала ла линия булып төшә. Был проекцияның төп миҫалы булып цилиндрик Меркатор проекцияһы (1569) тора, ул бөгөнгө көндә лә диңгеҙ диаграммалары өсөн ҡулланыла.

Тигеҙ ҙурлыҡтағы проекциялар

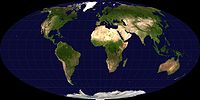
Тигеҙ ҙурлыҡтағы проекцияларҙа майҙан боҙолмай, әммә мөйөштәрҙең һәм формаларҙың боҙолоуы ҙур (юғары киңлектәрҙәге материктар бергә ҡушыла). Бындай проекцияла иҡтисади, тупраҡ һәм башҡа ваҡ масштаблы карталар өсөн ҡулланыла.

Ирекле проекциялар

Ирекле проекцияларҙа ла мөйөштәрҙең, майҙандың боҙолоуы бар, әммә тигеҙ ҙурлыҡтағы һәм тигеҙ мөйөшлө проекцияларҙағыға ҡарағанда күпкә кәмерәк, шуға күрә был проекциялар киң ҡулланыла.

Айырым айырым проекциялар осрағы булып айырым бер йүнәлештә араларҙы һаҡлаусы тигеҙ проекциялар тора: мәҫәлән, туранан-тура азимуталь проекция, унда полюс алыҫлығы дөрөҫ һүрәтләнә.

Нормаль селтәр параллелдәренең һәм меридиандарының төрө буйынса проекцияларҙы классификациялау

Цилиндрик проекция

Тура цилиндр проекцияларында параллелдәр һәм меридиандар бер-береһенә перпендикуляр булған параллель тура һыҙыҡтар менән һүрәтләнә. Шулай итеп, цилиндр проекцияларының тура мөйөшлө селтәре бирелә

Меридиандар араһындағы аралыҡ оҙонлоҡтар айырмаһына пропорциональ. Параллелдәр араһындағы аралыҡтар һүрәттең ҡабул ителгән характеры йәки ер өҫтө нөктәләрен цилиндрҙың ҡабырға йөҙөнә проектлау ысулы менән билдәләнә. Проекцияларҙы билдәләүҙән күренеүенсә, уларҙың меридиандар һәм параллелдәр селтәре ортогональ. Цилиндрлы проекцияларҙы конус түбәһе сикһеҙ булған конуслы проекцияларҙың айырым осрағы тип ҡарарға мөмкин.

Конуслы проекциялар

Боҙоҡлоу характеры буйынса конуслы проекциялар төрлө булырға мөмкин. Тигеҙ мөйөшлө һәм тигеҙ аралыҡлы проекциялар киң таралыу ала. Конуслы проекцияларҙың барлыҡҡа килеүен ер өҫтөнән конустың ҡабырға йөҙөнә, ер шарына (эллипсоида) ҡарата йүнәлешле итеп проектлау тип күҙ алдына килтерергә мөмкин.

Тура конуслы проекцияларҙа ер шары күсәрҙәре һәм конус күсәре тап килә.

Азимуталь проекциялар

Азимуталь проекцияларҙа параллелдәр концентрик түңәрәктәр менән һүрәтләнә, ә меридиандар үҙәктең туранан-тура шәлкемдәре менән күрһәтелә.

Псевдоконислы проекциялар

Псевдоконик проекцияларҙа параллелдәр концентрик түңәрәктәрҙең дуғалары менән һүрәтләнә, меридиандарҙың береһе уртаса тура һыҙыҡ тип атала, ә ҡалғандары уртасаға ҡарата симметрик булған кәкрелектәр менән бирелә.

Псевдоцилиндрик проекциялар

Псевдоцилиндрик проекцияларҙа бөтә параллелдәр параллель һыҙыҡтарҙан, урта меридиан параллелдәргә туранан-тура перпендикуляр, ә ҡалған меридиандарҙан кәкре һыҙыҡтар менән күрһәтелә. Урта меридиан — проекция симметрияһы күсәре булып тора.

Поликонуслы проекциялар

Поликонуслы проекцияларҙа экватор тура һыҙыҡ итеп һүрәтләнә, ә ҡалған параллелдәре эксцентрик түңәрәктәр дуғаларынан ғибәрәт. Меридиандар экваторға ҡарата үҙәк тура меридиан перпендикулярына ҡарата симметриялы кәкреләрҙән тора.

Шулай уҡ ҡарағыҙ

Масштаб
Математик картографія
Картографи проекциялары исемлеге

Иҫкәрмәләр

↑ Картографические проекции // Военная энциклопедия / Грачёв П. С.. — Москва: Военное издательство, 1995. — Т. 3. — С. 495.
↑ ^2,0 ^2,1 ^2,2 Картографические проекции // Казахстан. Национальная энциклопедия. — Алматы: «Қазақ энциклопедиясы», 2005. — Т. III. — ISBN 9965-9746-4-0.

Әҙәбиәт

Берлянт А. М. Картографический словарь. — М.: Научный мир, 2005. — 424 с. — ISBN 5-89176-309-5.

Һылтанмалар

Картографические проекции // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978. // БСЭ
Картографические проекции (неопр.). Математическая составляющая. Архивировано 16 мая 2020 года.
Картографические проекции (USGS Map Projections Poster) 2006 йыл 2 июнь архивланған.

[voen_enc1995-1] Картографические проекции // Военная энциклопедия / Грачёв П. С.. — Москва: Военное издательство, 1995. — Т. 3. — С. 495.

[КНЭ-2] 2,0 ^2,1 ^2,2 Картографические проекции // Казахстан. Национальная энциклопедия. — Алматы: «Қазақ энциклопедиясы», 2005. — Т. III. — ISBN 9965-9746-4-0.

[1]

[2]