Майҙан
| Майҙан | |
| Алдағы | оҙонлоҡ |
|---|---|
| Тәртип буйынса һуңыраҡ килеүсе | күләм |
| Дәүмәл билдәһе | S |
| Үлсәме | |
| Закон йәки теорема формулаһы | [1] |
| Обозначение в формуле | , һәм |
| Дәүмәл символы (LaTeX) | һәм |
| Вики-проект | Проект:Математика[d] |
| Рекомендуемая единица измерения | квадрат метр[d][2][3] |
| Майҙан | |
| , от франц. superficie | |
| Үлсәнеш |
L² |
|---|---|
| Үлсәү берәмеге | |
| СИ | |
| СГС | |
| Примечания | |
Майҙан — ике үлсәмле (яҫы йәки бөгөлгән) геометрик фигураның, был фигураның үлсәмен күрһәтеүсе, һанлы характеристикаһы[4]. Тарихи майҙанды иҫәпләү квадратура тип атала. Майҙаны булған фигура квадратланыусы тип атала. Ябай фигуралар өсөн майҙандың аныҡ ҡиммәте был төшөнсәгә ҡуйылған мөһим талаптарҙан килеп сыға (аҫтараҡ ҡарағыҙ). Бер үк майҙанлы фигуралар тигеҙ ҙурлыҡта тип аталалар. Геометрик фигураларҙың майҙанын иҫәпләүҙең дөйөм ысулын интеграль иҫәпләү бирҙе. Геометрик объекттарҙың киңерәк класы өсөн ҡулай булған күмәклек үлсәме теорияһы майҙан төшөнсәһенең дөйөмләштерелеүе булып тора.
Майҙандың ҡиммәтен яҡынса иҫәпләү өсөн практикалапалетка йәки махсус үлсәү приборы — планиметр ҡулланалар.
Майҙан төшөнсәһенең билдәләмәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]
Майҙан — түбәндәге үҙсәнлектәргә эйә булған функция[5][4]:
- Ыңғайлыҡ, йәғни майҙан тиҫкәре түгел;
- Аддитивлыҡ, йәғни фигураның майҙаны уны төҙөүсе, уртаҡ эске нөктәләре булмаған фигураларҙың майҙандары суммаһына тигеҙ;
- Инвариантлыҡ, йәғни конгруэнт фигураларҙың майҙандары тигеҙ;
- нормалаштырылғанлыҡ, йәғни берәмек квадраттың майҙаны 1-гә тигеҙ.
Майҙандың был билдәләмәһенән уның бер төрлөлөгө килеп сыға, йәғни фигураның бер өлөшөнөң майҙаны бөтә фигураның майҙанынан бәләкәй[5].
Иң башта майҙандың билдәләмәһе күпмөйөштәр өсөн бирелә, аҙаҡ ул квадратланыусы фигураларға киңәйтелә. Квадратланыусы тип, күпмөйөшкә ҡамап булған һәм уға күпмөйөштө ҡамап булған фигура атала, шуның менән бергә, ике күпмөйөштөң дә майҙандары ирекле бик бәләкәй дәүмәлгә айырылалар. Бындай фигуралар шулай уҡ Жордан буйынса үлсәнмәле тип аталалар[4]. Яҫылыҡта бөтөн һандағы берәмек квадраттарҙан тормаған фигуралар өсөн, майҙан сикләмәле күсеү ярҙамында табыла; был осраҡта, фигура үҙе лә, шулай уҡ уның сиге лә өлөшләтә-шыма булыуы талап ителә[6]. Квадратланмаусы яҫы фигуралар була[4]. Юғарыла тәҡдим ителгән майҙандың аксиоматик билдәләмәһен яҫы фигуралар осрағында ғәҙәттә конструктив билдәләмә менән тулылындыралар, унда асылда палетка ярҙамында майҙанды иҫәпләү башҡарыла. Шуның менән бергә, теүәлерәк иҫәпләүҙәр өсөн, артабанғы аҙымда яғының оҙонлоғо алдағы палетканың яғынан ун тапҡыр бәләкәйерәк булған палетканы ҡулланалар[7].
Квадратланыусы яҫы фигураның майҙаны бар һәм ул берҙән бер. Дөйөм күмәклектәргә киңәйтелгән майҙан төшөнсәһе, үлсәм теорияһы шөғөлләнгән Лебег буйынса үлсәнмәле күмәклектәр төшөнсәһенә килтерә. Артабан майҙан үҙсәнлектәре уның берҙән берлеген тәьмин итмәгән дөйөмөрәк кластар барлыҡҡа килә[4].
Дөйөм мәғәнәлә майҙан төшөнсәһе аҫтында n-үлсәмле (Евклид йәки Риман) арауығында k-үлсәмле йөҙҙөң һанлы характеристикаһын аңлайҙар, айырым осраҡта, өс үлсәмле арауыҡта ике үлсәмле йөҙҙөң характеристикаһы[4].
Майҙанды иҫәпләүҙең дөйөм ысулы
[үҙгәртергә | сығанаҡты үҙгәртеү]Яҫы фигураның майҙаны
[үҙгәртергә | сығанаҡты үҙгәртеү]Практикала йыш ҡына өлөшләтә-шыма сикле фигураның майҙанын табырға тура килә. Математик анализ бындай мәсьәләләрҙе сисеүҙең универсаль ысулын тәҡдим итә.
Декарт координаталары
[үҙгәртергә | сығанаҡты үҙгәртеү]
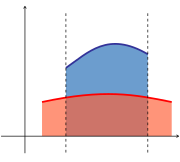
интервалында өҙлөкһөҙ функцияның графигы һәм горизонталь күсәр менән сикләнгән майҙан был функциянан аныҡ интеграл булараҡ иҫәпләнергә мөмкин:
интервалында ике өҙлөкһөҙ функциялары графиктары араһындағы майҙан был функцияларҙан аныҡ интегралдар айырмаһы булараҡ табыла:
Поляр координаталар
[үҙгәртергә | сығанаҡты үҙгәртеү]Поляр координаталарҙа: функцияһының графигы һәм нурҙары менән сикләнгән майҙан түбәндәге формула буйынса иҫәпләнә:
- .
Йөҙҙөң майҙаны
[үҙгәртергә | сығанаҡты үҙгәртеү]Өс үлсәмле арауыҡта өлөшләтә-шыма йөҙҙөң майҙанын табыу өсөн һәр нөктәлә тейеүсе яҫылыҡтарға ортогональ проекцияларҙы ҡулланалар, шунан һуң сикләмәле күсеү башҡарыла. Һөҙөмтәлә, вектор-функцияһы менән бирелгән A ҡалтайған йөҙөнөң майҙаны икеләтә интеграл менән бирелә[4]:
Шул уҡ координаталарҙа:
Бында .
Майҙандар теорияһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Майҙандар теорияһы өлөшләтә-шыма батырылмалы k-үлсәмле майҙан билдәләмәһен дөйөмөрәк арауыҡтарға таратыу менән бәйле дөйөмләштереүҙәрҙе өйрәнеү менән шөғөлләнә. f өлөшләтә-шыма батырылыу өсөн майҙанды юғарыла күрһәтелгән ысулға оҡшаш рәүештә иҫәпләйҙәр, шуның менән бергә майҙандың ыңғайлыҡ, аддитивлыҡ, нормалаштырылғанлыҡ кеүек, шулай уҡ бер нисә яңы үҙсәнлектәре һаҡлана.
Майҙан үлсәү берәмектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]
Үлсәү берәмектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]- Квадрат метр, сығарылма берәмек (СИ) Халыҡ-ара берәмектәр системаһында; 1 м² = 1 са (сантиар);
- Квадрат километр, 1 км² = 1 000 000 м²;
- Гектар, 1 га = 10 000 м²;
- Ар (сотка), 1 а = 100 м²:
- Квадрат дециметр, 100 дм² = 1 м²;
- Квадрат сантиметр, 10 000 см² = 1 м²;
- Квадрат миллиметр, 1 000 000 мм² = 1 м²;
- Барн, 1 б = 10−28 м².
Боронғо урыҫ берәмектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]- Квадрат саҡрым = 1,13806 км²
- Дисәтинә = 10925,4 м²
- Күбә = 0,1 дисәтинә — бесән бакуйын күбәләр менән үлсәгәндәр.
- Квадрат сажин = 4,55224 м²
Налогтарҙы иҫәпләгәндә ер үлсәме булып выть, һуҡа, урыу хеҙмәт иткән, уларҙың үлсәме ерҙең сифатына һәм хужаһының социаль хәленә бәйле булған: коробья, арҡан, жеребья һәм башҡалар.
Боронғо үлсәү берәмектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]Башҡалар
[үҙгәртергә | сығанаҡты үҙгәртеү]- Рай = 1600 м² (40 м × 40 м).
- Квадрат парсек
- Планк майҙаны () ≈ 2,612099 · 10−70 м2
Ябай фигураларҙың майҙандарын иҫәпләү формулалары
[үҙгәртергә | сығанаҡты үҙгәртеү]| Фигура | Формула | Үҙгәреүсәндәр |
|---|---|---|
| Төҙөк өсмөйөш | — өсмөйөш яғының оҙонлоғо | |
| Тура мөйөшлө өсмөйөш | и — өсмөйөштөң катеттары | |
| Ирекле өсмөйөш | — өсмөйөштөң яғы, — был яҡҡа төшөрөлгән бейеклек | |
| һәм — теләһә ниндәй ике яғы, — улар араһындағы мөйөшө | ||
| (Герон формулаһы) |
, һәм — өсмөйөштөң яҡтары, — ярым периметр | |
| , , — өсмөйөш түбәләренең координаталары (түбәләрҙе сәғәт уғы йүнәлешендә урап үткәндә ыңғай һөҙөмтә алабыҙ, кире осраҡта тиҫкәре) | ||
| Квадрат | — квадрат яғының оҙонлоғо | |
| Тура дүртмөйөш | һәм — тура дүртмөйөштөң яҡтары оҙонлоғо (уның оҙонлоғо һәм киңлеге) | |
| Ромб | һәм — ромбтың диагоналдәре оҙонлоғо | |
| Параллелограмм | һәм — яғы һәм ярашлы рәүештә был яҡҡа төшөрөлгән бейеклеге оҙонлоғо | |
| һәм — параллелограммдың эргәләш яҡтары, — улар араһындағы мөйөш | ||
| Трапеция | и — трапецияның нигеҙҙәре, — трапецияның бейеклеге | |
| Ирекле дүртмөйөш | (Брахмагупта формулаһы) |
, , , — дүртмөйөштөң яҡтары, — уның ярым периметры, — дүртмөйөштөң ҡаршы ятыусы мөйөштәренең ярымсуммаһы |
| Төҙөк алтымөйөш | — алтымөйөш яғының оҙонлоғо | |
| Төҙөк һигеҙмөйөш | — һигеҙмөйөш яғының оҙонлоғо | |
| Төҙөк күпмөйөш | — периметры, — яҡтарының һаны | |
| Ирекле күпмөйөш (ҡабарынҡы һәм ҡабарынҡы булмаған) | (трапециялар ысулы) |
} |
Түңәрәктең, уның өлөштәренең, түңәрәккә ҡамалған һәм ҡамаусы фигураларҙың майҙаны
[үҙгәртергә | сығанаҡты үҙгәртеү]| Фигура | Формула | Үҙгәреүсәндәр |
|---|---|---|
| Түңәрәк | йәки | — түңәрәктең радиусы, — диаметры |
| Түңәрәк секторы | — түңәрәктең радиусы, — секторҙың үҙәк мөйөшө (радиандарҙа) | |
| Түңәрәк сегменты | — түңәрәктең радиусы, — сегменттың үҙәк мөйөшө (радиандарҙа) | |
| Эллипс | , — эллипстың ҙур һәм бәләкәй ярымкүсәре | |
| Әйләнәгә ҡамалған өсмөйөш | , һәм — өсмөйөштөң яҡтары, — ҡамаусы әйләнәнең радиусы | |
| Әйләнәгә ҡамалған дүртмөйөш | (Брахмагупта формулаһы) |
, , , — дүртмөйөштөң яҡтары, — уның ярым периметры |
| Әйләнәне ҡамаусы күпмөйөш | — күпмөйөшкә ҡамалған әйләнәнең радиусы, — күпмөйөштөң периметры | |
| Әйләнәне ҡамаусы тура мөйөшлө трапеция | , — трапецияның нигеҙҙәре |
Арауыҡта есемдәрҙең йөҙҙәре майҙаны
[үҙгәртергә | сығанаҡты үҙгәртеү]| Есем | Формула | Үҙгәреүсәндәр |
|---|---|---|
| Тура түңәрәк цилиндрҙың тулы йөҙө | һәм — ярашлы рәүештә радиус һәм бейеклек | |
| Тура түңәрәк цилиндрҙың эргә йөҙө | ||
| Тура түңәрәк конустың тулы йөҙө | һәм — ярашлы рәүештә эргә йөҙөнөң радиусы һәм төҙөүсеһе | |
| Тура түңәрәк конустың эргә йөҙө | ||
| Сфераның (шарҙың) йөҙө | йәки | һәм — ярашлы рәүештә радиус һәм диаметр |
| Тура призманың эргә йөҙө | — нигеҙенең периметры, — бейеклек | |
| Ирекле призманың тулы йөҙө | — нигеҙенең майҙаны — эргә йөҙөнөң майҙаны |
Тарихи очерк
[үҙгәртергә | сығанаҡты үҙгәртеү]Яҫы фигуралар майҙаны
[үҙгәртергә | сығанаҡты үҙгәртеү]Оҙаҡ йылдар майҙан билдәләмә талап итмәүсе төп төшөнсә булып һаналған. Математиктарҙың төп маҡсаты булып майҙанды иҫәпләү торған, шуның менән бергә майҙандың төп үҙсәнлектәре билдәле булған[5]. Боронғо Египетта тура дүртмөйөштәрҙең, тура мөйөшлө өсмөйөштәрҙең һәм трапецияларҙың майҙандарын иҫәпләүҙең теүәл ҡағиҙәләре ҡулланылған, ирекле дүртмөйөштөң майҙаны ҡаршы ятыусы яҡтары парҙарының ярым суммалары ҡабатландығы итеп яҡынса иҫәпләнгән. Бындай яҡынса формуланы ҡулланыу шуның менән бәйле булған, майҙанын табырға кәрәк булған участкалар нигеҙҙә тура дүртмөйөшкә яҡын була, һәм был осраҡта яңылышлыҡ бик бәләкәй була. Математика тарихсыһы А. П. Юшкевич, күп египетлылар яҡынса формула ҡулланғандарын белмәгән булырға ла мөмкин тип фаразлай. Ринд папирусындағы 50-се мәсьәләлә түңәрәктең майҙанын иҫәпләү формулаһы бар, унда түңәрәктең майҙаны яғы түңәрәк диаметрының 8/9 өлөшөнә тигеҙ булған квадраттың майҙанына тигеҙ тип иҫәпләнә[8]. Шундай уҡ формулалар менән Вавилонда ла ҡулланғандар, әммә түңәрәктең майҙаны өсөн яҡынса иҫәпләү бик теүәл булмаған. Бынан тыш, вавилонлылар яғы бер берәмеккә тигеҙ булған төҙөк биш-, алты- һәм етемөйөштөң майҙанын яҡынса иҫәпләй алғандар. Алтмышарлы иҫәпләү системаһында уларға ярашлы рәүештә 1,40, 2,37,20 и 3,41 һандары ярашлы булған [9].
Майҙанды иҫәпләүҙең төп ысулы булып, майҙаны бирелгән күпмөйөшлө фигураның майҙанына тигеҙ булған квадрат төҙөү торған, атап әйткәндә, Евклидтың «Башланғыстарының» тура һыҙыҡлы фигураларҙың планиметрияһына бағышланған I китабында, өсмөйөш, нигеҙе һәм бейеклеге уныҡына тигеҙ булған тура дүртмөйөштөң яртыһы менән тигеҙ ҙурлыҡта тип иҫбат ителә [10]. Ике тигеҙ өлөштәрҙән торған фигуралар тигеҙ ҙурлыҡта булыуына нигеҙләнгән тарҡатыу ысулы, параллелограмдарҙың һәм теләһә ниндәй күпмөйөштәрҙең майҙандарын иҫәпләргә мөмкинлек биргән[7].
Артабанғы аҙым булып түңәрәктең, түңәрәк секторының, соҡорҙарҙың һәм башҡа фигураларҙың майҙанын иҫәпләү торған. Был осраҡта иҫәпләүҙең нигеҙен күпмөйөштәр менән файҙаланып бөтөү ысулы тәшкил иткән[4][7], сикләмәләр теорияһы шунан баш алған да инде. Ысул, әкренләп ҙурая барғанда бөтә талап ителгән майҙанды «файҙаланып (тултырып) бөткән» майҙандар эҙмә-эҙлелеген төҙөүҙән тора. Үҙенең исемен XVII быуатта ғына алған файҙаланып бөтөү ысулы, Евдокс — Архимедтың өҙлөкһөҙлөк аксиомаһына нигеҙләнгән һәм Евдокс Книдскийҙыҡы тип иҫәпләнә, ул ошо ысул ярҙамында, түңәрәктәрҙең майҙандарының сағыштырмаһы уларҙың диаметрҙарының сағыштырмаһына тигеҙ булыуын күрһәткән. Ысул Евклидтың "Башланғыстар"ында һүрәтләнә: Евдокстың аксиомаһы V китапта әйтеп бирелә, ә файҙаланып бөтөү ысулы үҙе һәм уға нигеҙләнгән нисбәттәр — XII китапта[10]. Архимед ысулды ҡулланыуҙа үтә камиллыҡҡа өлгәшә, ул был ысул ярҙамында парабола сегментының майҙанын һәм башҡа майҙандарҙы иҫәпләгән[11][12]. Архимедтың «О спиралях» хеҙмәтендә төрлө спиралдәр уралмаларының майҙандарына һәм уларҙың сағыштырмаларына ҡағылышлы күп раҫлауҙар бар[13]. Талап ителгән майҙанды йәки күләмде табыу өсөн ҡамалған һәм ҡамаусы фигураларҙың майҙандарын һәм күләмдәрен файҙаланыу Архимедтың идеяһы булып тора[14].
Һиндостанлылар башта дүртмөйөштәрҙе иҫәпләү өсөн шул уҡ египетлылар һәм гректар файҙаланған формуланы ҡулланалар. Брахмагупта дүртмөйөш майҙанын иҫәпләү өсөн, әйләнәгә ҡамалған дүртмөйөш өсөн дөрөҫ булған, уның ярым периметры аша күрһәтелгән формуланы ҡулланған. Майҙанды иҫәпләү формулалары ғәҙәттә иҫбат ителмәгәндәр, ләкин асыҡ күренеп торған һүрәттәрҙә күрһәтелгәндәр[15]. Брахмагупта формулаһы өсмөйөш майҙаны өсөн Герон формулаһының аналогы булып тора, был формуланы ул үҙенең «Метрика»һында килтерә[16].
Файҙаланып бөтөү ысулы тик XVII быуатта ғына үҫеш ала һәм дөйөмләштерелә. 1604 йылда Валерио «Есемдәрҙең ауырлыҡ үҙәге тураһында өс китап» хеҙмәтендә, параллелограмдарҙан төҙөлгән ҡамалған һәм ҡамаусы фигуралар майҙандары араһындағы айырманы бирелгән теләһә ниндәй майҙандан бәләкәй итеп була тигән теореманы киң ҡуллана[17]. Астрономик иҫәпләүҙәр өсөн эллипстың майҙанын иҫәпләй белергә кәрәк булған Кеплер етди алға китеш яһай. Кеплер майҙанды «һыҙыҡтар суммаһы» итеп ҡарай, һәм эллипсты бер градус аҙым менән һыҙып сығып, [18], булыуын күрһәтә. Кавальери, «бүленмәүселәр ысулы» тип аталған оҡшаш ысулды нигеҙләп, яҫы фигураларҙың майҙандарын, фигураны параллель тура һыҙыҡтар менән киҫеүҙе ҡулланып сағыштырған[19]. Яҫы фигураларҙың майҙандарын табыу өсөн алынманы ҡулланыу универсаль ысул булып тора. Алынма ярҙамында Кавальери принцибы иҫбатлана, уның буйынса, әгәр ике яҫы фигураның һәр береһен бирелгән тура һыҙыҡҡа параллель тура һыҙыҡ менән киҫкәндә, бер үк оҙонлоҡтағы киҫектәр килеп сыҡһа, был ике яҫы фигураның майҙандары тигеҙ була. Был принцип интеграль иҫәпләү формалашыуҙан күп алда билдәле була[4][7].
Йөҙҙөң майҙаны
[үҙгәртергә | сығанаҡты үҙгәртеү]Кәкре йөҙҙәрҙең майҙанын иҫәпләү менән Архимед шөғөлләнә, атап әйткәндә шарҙың йөҙөнөң майҙанын иҫәпләй[14]. Дөйөм осраҡта йөҙҙөң майҙанын табыу өсөн йәйелмә менән дә (сфера өсөн яраҡһыҙ), күпҡырлы йөҙҙөр менән яҡынайтыуҙы ла, йәғни файҙаланып бөтөү ысулының аналогы, файҙаланып булмай. Һуңғыһын Шварц күрһәтә, ул цилиндрҙың эргә йөҙө өсөн төрлө һөҙөмтәләргә килтергән (Шварц итеге тип аталған) эҙмә-эҙлелек төҙөй[4][20].
Майҙанды иҫәпләүҙең дөйөм ысулын XIX—XX быуаттар араһында Минковский тәҡдим итә, ул һәр йөҙ өсөн йоҡа даими ҡалынлыҡтағы «ҡаплап алған ҡатлам» төҙөй, ул саҡта йөҙҙөң майҙаны яҡынса был ҡатламдың күләменең уның ҡалынлығына бүлендегенә тигеҙ була. Ҡалынлығы нулгә ынтылғанда сикләмәгә күсеү майҙандың теүәл ҡиммәтен бирә. Ләкин, Минковский буйынса майҙан өсөн аддитивлыҡ үҙсәнлеге һәр саҡ үтәлмәй. Был билдәләмәне дөйөмләштереү Минковский буйынса һыҙыҡ төшөнсәһенә һәм башҡаларға килтерә[21].
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ 3-3 // Quantities and units—Part 3: Space and time (ингл.) — 1 — ISO, 2006. — 19 p.
- ↑ 3-3 // Quantities and units — Part 3: Space and time, Grandeurs et unités — Partie 3: Espace et temps (ингл.) — 2 — ISO, 2019. — 11 p.
- ↑ 3-3.a // Quantities and units—Part 3: Space and time (ингл.) — 1 — ISO, 2006. — 19 p.
- ↑ 4,00 4,01 4,02 4,03 4,04 4,05 4,06 4,07 4,08 4,09 Площадь // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
- ↑ 5,0 5,1 5,2 Геометрия, 1966, с. 7—13
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186—224. — 800 с.
- ↑ 7,0 7,1 7,2 7,3 Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977, c.2—9
- ↑ История математики, т. I, 1970, с. 30—32
- ↑ История математики, т. I, 1970, с. 47—53
- ↑ 10,0 10,1 История математики, т. I, 1970, с. 111—114
- ↑ Исчерпывания метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
- ↑ История математики, т. I, 1970, с. 101—105
- ↑ Boyer & Merzbach, 2010, p. 127—128
- ↑ 14,0 14,1 История математики, т. I, 1970, с. 117—124
- ↑ История математики, т. I, 1970, с. 197—198
- ↑ Boyer & Merzbach, 2010, p. 172, 219
- ↑ История математики, т. II, 1970, с. 131—135
- ↑ История математики, т. II, 1970, с. 166—171
- ↑ История математики, т. II, 1970, с. 174—181
- ↑ В. Н. Дубровский, В поисках определения площади поверхности. Квант. 1978. № 5. С.31—34.
- ↑ В. Н. Дубровский, Площадь поверхности по Минковскому. Квант. 1979. № 4. С.33—35.
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]- Энциклопедия элементарной математики. Книга пятая. Геометрия / под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М.: Наука, 1966. — 624 с.
- Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2.
- История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени.
- История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. II: Математика XVII столетия.
- Boyer C. B., Merzbach U. C. A History of Mathematics. — John Wiley & Sons, 2010. — 640 p. (инг.)







![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






























































