Квадрат

Квадрат
Двойственнен к	квадрат
Символ Шлефли	{4}
Грань политопа	ҡабырға
Вики-проект	Проект:Математика[d]
Квадрат Викимилектә

Квадра́т — төҙөк дүртмөйөш, йәғни бөтә мөйөштәре тигеҙ һәм бөтә яҡтары тигеҙ булған дүртмөйөш.

Квадрат

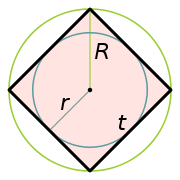
Квадраттың үҙсәнлектәре

1. Яҡтарының оҙонлоҡтары тигеҙ.
2. Квадраттың бөтә мөйөштәре лә тура.
3. Квадраттың диагоналдәре тигеҙ, үҙ-ара перпендикуляр, киҫешеү нөктәһендә урталай бүленәләр һәм мөйөштәренең биссектрисалары булып торалар.

Үҙсәнлектәре

• $t$ — квадраттың яғы, $R$ — ҡамаусы әйләнәнең радиусы, $r$ — ҡамалған әйләнәнең радиусы булһын. Ул саҡта ҡамаусы һәм ҡамалған әйләнәләрҙең үҙәге уның диагоналдәре киҫешкән нөктә менән тап килә һәм
  • квадратҡа ҡамалған әйләнәнең радиусы квадрат яғының яртыһына тигеҙ:

    $r={\frac {t}{2}}$,

  • квадратты ҡамаусы әйләнәнең радиусы квадрат диагоналенең яртыһына тигеҙ:

    $R={\frac {\sqrt {2}}{2}}t$,

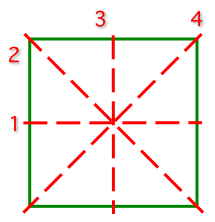
• Квадрат бөтә дүртмөйөштәр араһында иң күп симметрияға эйә. Уның
  • дүртенсе тәртиптәге бер симметрия күсәре (квадрат яҫылығына перпендикуляр һәм уның үҙәге аша үтеүсе күсәр);
  • икенсе тәртиптәге дүрт симметрия күсәре бар (яҫы фигура өсөн сағылышҡа эквивалентлы), шуларҙың икәүһе квадраттың диагоналдәре буйлап үтә, ә ҡалған икәүһе — яҡтарына параллель үтә.
• Квадраттың диагоналдәре тигеҙ, үҙ-ара перпендикуляр, киҫешеү нөктәһендә урталай бүленәләр һәм мөйөштәренең биссектрисалары булып торалар.

Квадраттың майҙаны һәм уның яғының оҙонлоғо

Симметрия һыҙыҡтары

Квадраттың периметры

• • Квадраттың периметры тигеҙ:

    $P=4t=4{\sqrt {2}}R=8r$,

Квадраттың майҙаны

Бында тап квадратҡа хас булған формулалар килтерелгән. Шулай уҡ ҡара

ирекле дүртмөйөштәрҙең майҙандары өсөн формулалар.

• • Квадраттың майҙаны $S$

    $S=t^{2}=2R^{2}=4r^{2}$ тигеҙ.

Евклид булмаған геометрия

Евклид булмаған геометрияла квадрат (киңерәк) — дүрт тигеҙ яғы һәм тигеҙ мөйөштәре булған күпмөйөш.

Квадратты циркуль һәм линейка ҡулланып төҙөү

Квадратты ирекле ҡағыҙ киҫәгенән бөкләү

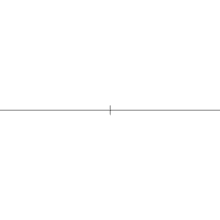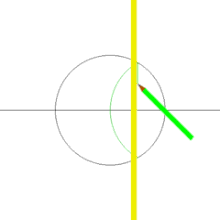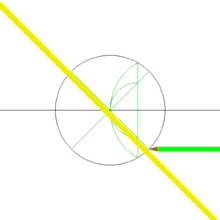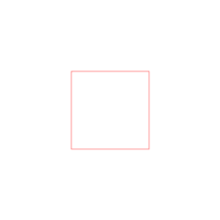
Квадраттарҙың күп төрлөлөгө

Биш төҙөк күпҡырҙарҙың береһе — кубтың ҡырҙары квадрат була.

Графтар: K₄ тулы граф йыш ҡына алты ҡабырғалы квадрат рәүешендә һүрәтләнә.

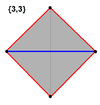3-симплекс (3D)

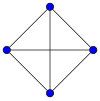
Шахмат таҡтаһы квадрат формаһында һәм ике төҫтәге 64 квадратҡа бүленгән. Халыҡ-ара шашка өсөн квадрат таҡта ике төҫтәге 100 квадратҡа бүленгән. Боксёр рингы квадрат формаһында, уйын өсөн майҙансыҡ квадрат.

Лим флагы квадраты икеҡара һәм ике һары квадратҡа бүленгән, гавандә карапта күтәрелгәндә, карап карантинда тигәнде аңлата.

Лим флагы

Шулай уҡ ҡара

• Дельтоид
• Берәмек квадрат
• Квадрат тип 2-се дәрәжәгә күтәреү атала
• Түңәрәк квадратураһы
• Квадратты квадратлау
• Тура дүртмөйөш
• Ромб
• Вариньон параллелограмы
• Тебо теоремаһы 1
• Трапеция
• Өсмөйөш
• Дүртмөйөш
• Marching squares

Һылтанмалар

• Квадрат, геометрическая фигура // Брокгауз һәм Ефрондың энциклопедик һүҙлеге: 86 томда (82 т. һәм 4 өҫтәмә том). — СПб., 1890—1907. (рус.)

<onlyinclude>

<onlyinclude>