Дүртмөйөш
| Дүртмөйөштәр | |||||||
|---|---|---|---|---|---|---|---|
| ┌─────────────┼────────────┐ | |||||||
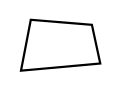
| ҡабарынҡы түгел | ҡабарынҡы | үҙ-үҙе менән киҫешеүсе | |||||

|
|

| |||||
| ┌─────────────┼─────────────┐ | |||||||
|

|
| |||||
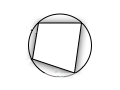
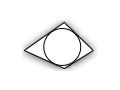
| ҡамалған | трапеция | ҡамаусы | |||||
| | ┌───────────┤ | | | ||||||
 тигеҙ эргәле трапеция |
 параллелограмм |
 антипараллелограмм |
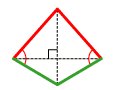 ҡабарынҡы ромбоид (дельтоид) | ||||
| └─────┬─────┘ | └─────┬─────┘ | ||||||
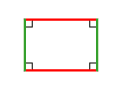 тура дүртмөйөш |
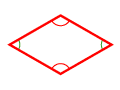 ромб | ||||||
| └──────────┬─────────┘ | |||||||
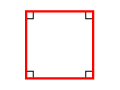 | |||||||
Дүртмөйөш (грек. τετραγωνον) — ул, өсәүһе бер тура һыҙыҡта ятмаған дүрт нөктәнән (түбәләре), һәм был нөктәләрҙе эҙмә-эҙ тоташтырыусы дүрт киҫектән (яҡтары) торған геометрик фигура (күпмөйөш). ҡабарынҡы һәм ҡабарынҡы булмаған дүртмөйөштәр була, ҡабарынҡы булмаған дүртмөйөш үҙ-үҙе менән киҫешеүсе булырға мөмкин (һүрәтте ҡарағыҙ).
Дүртмөйөш төрҙәре[үҙгәртергә | сығанаҡты үҙгәртеү]
- Параллелограмм — ҡапма-ҡаршы яҡтары пар-пар тигеҙ һәм параллель булған дүртмөйөш;
- Тура дүртмөйөш — бөтә мөйөштәре лә тура булған дүртмөйөш;
- Ромб — бөтә яҡтары ла тигеҙ булған дүртмөйөш;
- Квадрат — бөтә мөйөштәре лә тура һәм бөтә яҡтары ла тигеҙ булған дүртмөйөш;
- Трапеция — ике ҡаршы ятҡан яғы параллель булған дүртмөйөш;
- Дельтоид — ике пар эргәләш яҡтары тигеҙ булған дүртмөйөш.
- Антипараллелограмм, йәки контрпараллелограмм — һәр ике ҡаршы ятыусы яҡтары үҙ-ара тигеҙ, ләкин параллелограммдан айырмалы рәүештә параллель булмаған, ә антипараллель булған дүртмөйөш.
Ҡайһы бер тамғалауҙар һәм ҡыҫҡартыуҙар[үҙгәртергә | сығанаҡты үҙгәртеү]
«Дүртмөйөш» һүҙе урынына ҡайһы бер тамғалауҙар һәм ҡыҫҡартыуҙар ҡуланылыуы мөмкин: дүртмөй, «» йәки « ♢» символдары [1].
Ҡайһы бер симметрик дүртмөйөштәр[үҙгәртергә | сығанаҡты үҙгәртеү]

Һүрәттә ҡайһы бер симметрик дүртмөйөштәр, уларҙың бер-береһенә күсеүе, шулай уҡ уларға дуал дүртмөйөштәр күрһәтелгән. Һүрәттәге тамғалауҙар:
- Kite (змей) — дельтоид (ромбоид)
- Parallelogram — параллелограмм
- Irregular quadrilateral — дөрөҫ булмаған дүртмөйөш
- Rhombus — ромб
- Rectangle — тура дүртмөйөш
- Square — квадрат
- Gyrational Square — әйләнеүсе квадрат
- Isosceles Trapezoid — тигеҙ эргәле трапеция
Тулы дүртъяҡ[үҙгәртергә | сығанаҡты үҙгәртеү]

Дүртъяҡ атамаһы дүртмөйөш атамаһына эквивалентлы булырға мөмкин булһа ла, уға йыш ҡына өҫтәмә мәғәнә һалалар. Тулы дүртъяҡ тип бер ниндәй икәүһе параллель булмаған һәм бер ниндәй өсәүһе бер нөктә аша үтмәгән дүрт тура һыҙыҡ атала. Бындай конфигурация Евклид геометрияһының ҡайһы бер раҫлауҙарында (мәҫәлән, Менелай теоремаһы, Гаусс тура һыҙығы, Обер тура һыҙығы, Микель тура һыҙығы һәм башҡалар) осрай, уларҙа йыш ҡына бөтә тура һыҙыҡтар ҙа бер береһен алмаштырыусан булалар.
Мөйөштәре суммаһы[үҙгәртергә | сығанаҡты үҙгәртеү]
Үҙ-үҙен киҫмәүсе дүртмөйөштөң мөйөштәре суммаһы 360°-ҡа тигеҙ.
Оҙонлоҡ нисбәттәре[үҙгәртергә | сығанаҡты үҙгәртеү]
Дүртмөйөш тигеҙһеҙлеге[үҙгәртергә | сығанаҡты үҙгәртеү]
Дүртмөйөштөң теләһә ниндәй ике яғының айырмаһы модуле ҡалған ике яғының суммаһынан ҙур түгел.
- .
Эквивалентлы: теләһә ниндәй дүртмөйөштә өс яғының оҙонлоҡтары суммаһы дүртенсе яғынан кәм түгел, йәғни [2]:
- ;
- ;
- ;
- .
Дүртмөйөш тигеҙһеҙлегендә тигеҙлек, дүртмөйөш боҙолған булғанда ғына, йәғни уның бөтә дүрт түбәһе бер тура һыҙыҡта ятҡанда ғына үтәлә.
Птолемей тигеҙһеҙлеге[үҙгәртергә | сығанаҡты үҙгәртеү]
Ҡабарынҡы дүртмөйөштөң яҡтары һәм диагоналдәре өсөн Птолемей тигеҙһеҙлеге үтәлә:
шуның менән бергә тигеҙлек үтәлә шул саҡта һәм тик шул саҡта ғына, әгәр ҡабарынҡы дүртмөйөш әйләнәгә ҡамалған булһа йәки уның түбәләре бер тура һыҙыҡта ятһалар.
Гаусс теоремаһы[үҙгәртергә | сығанаҡты үҙгәртеү]
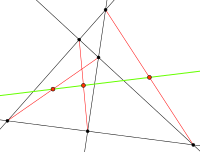
Әгәр дүртмөйөштә ике пар ҡаршы ятҡан яҡтары параллель булмаһа, уның ике диагоналенең уртаһы, ике пар ҡаршы ятҡан яҡтары киҫешкән ике нөктәне тоташтырыусы киҫектең уртаһы аша үтеүсе тура һыҙыҡта ята (һүрәттә нөктәләр ҡыҙыл төҫ менән күрһәтелгән). Был тура һыҙыҡ Гаусс тура һыҙығы тип атала (һүрәттә ул йәшел төҫ менән бирелгән). Шуның менән бергә Гаусс тура һыҙығы һәр саҡ Обер тура һыҙығына перпендикуляр.
Дүртмөйөштөң яҡтары һәм диагоналдәре араһында нисбәт[үҙгәртергә | сығанаҡты үҙгәртеү]
Яҫылыҡта ирекле рәүештә алынған дүрт нөктә араһында парлап алынған алты алыҫлыҡ түбәндәге нисбәт менән бәйле:
- .
Был нисбәтте билдәләүсе күренешендә күрһәтергә мөмкин:
Иҫкәрмә. Һуңғы билдәләүсе 288 ҡабатлаусыһына тиклем аныҡлыҡ менән Кэли-Менгер билдәләүсеһе ярҙамында ҡабырғаларының оҙонлоҡтары аша тетраэдр күләме квадраты өсөн аңлатма булып тора. Әгәр тетраэдр яҫылыҡҡа һалынһа, ул саҡта уның күләме нулгә тигеҙ һәм ул дүртмөйөшкә әйләнә. Ҡабырғаларының оҙонлоғо дүртмөйөштөң яҡтарының йәки диагоналдәренең оҙонлоғо була.
Бретшнайдер нисбәттәре[үҙгәртергә | сығанаҡты үҙгәртеү]
Бретшнайдер нисбәттәре — ябай (үҙ-үҙе менән киҫешмәгән) дүртмөйөштөң яҡтары a, b, c, d һәм ҡаршы ятыусы мөйөштәре һәм диагоналдәре e, f араһындағы нисбәт:
- ,
- ,
- .
Дүртмөйөштөң урта һыҙыҡтары тураһында теоремалар[үҙгәртергә | сығанаҡты үҙгәртеү]
G, I, H, J — ABCD ҡабарынҡы дүртмөйөшөнөң яҡтарының уртаһы, ә E, F — диагоналдәренең уртаһы булһын, ти. Өс GH, IJ, EF киҫектәрен ярашлы рәүештә дүртмөйөштөң беренсе, икенсе һәм өсөнсө урта һыҙыҡтары тип атайыҡ. Уларҙың тәүге икәүһен шулай уҡ бимедианалар тип тә атайҙар (bimedians[3])[4]
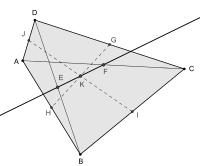
- Дөйөмләштерелгән Ньютон теоремаһы. Дүртмөйөштөң бөтә өс урта һыҙығы бер нөктәлә (түбәләре центроидында киҫешәләр («vertex centroid»)[4]) һәм был нөктә менән урталай бүленәләр.
- Ҡабарынҡы дүртмөйөштөң ике диагоналенең урталары E һәм F, шулай уҡ түбәләре центроиды K бер EFтура һыҙығында яталар. Был тура һыҙыҡ Ньютон тура һыҙығы тип атала.
- Вариньон теоремаһы (геометрия)[2]:
- GIHJ, EHFG, JEIF дүртмөйөштәре параллелограммдар булалар һәм Вариньон параллелограммдары тип аталалар. Уларҙың беренсеһен Вариньондың ҙур параллелограммы тип атайыҡ.
- Вариньондың бөтә өс параллелограммының үҙәктәре бирелгән дүртмөйөштөң яҡтарының урталарын тоташтырыусы киҫектең уртаһында ята (ҡаршы ятыусы яҡтарының урталарын тоташтырыусы киҫектәр — Вариньон параллелограммы диагоналдәре ошо уҡ нөктәлә киҫешә).
- Вариньондың ҙур параллелограммы периметры бирелгән дүртмөйөш диагоналдәре суммаһына тигеҙ.
- Вариньондың ҙур параллелограммы майҙаны бирелгән дүртмөйөшөнөң майҙаны яртыһына тигеҙ, йәғни
- .
- Бирелгән дүртмөйөшөнөң майҙаны дүртмөйөштөң беренсе һәм икенсе урта һыҙыҡтарының улар араһындағы мөйөш синусына ҡабатландығына тигеҙ, йәғни
- .
- Дүртмөйөштөң өс урта һыҙыҡтары квадраттары суммаһы уның бөтә яҡтарының һәм диагоналдәренең квадраттары суммаһының сирегенә тигеҙ:
- .
- Ҡалып:Якорь2: дүртмөйөштөң диагоналдәре урталары араһындағы алыҫлыҡтың дүртләтелгән квадраты яҡтары квадраттары суммаһынан уның диагоналдәре квадраттары суммаһын алғанға тигеҙ.
- Математик рәүештә һулдағы һоро ABCD дүртмөйөшлө һүрәт өсөн Ҡалып:Якорь2 ошолай күренештә яҙыла:
- .
- Һәр береһе дүртмөйөштөң түбәһен ҡалған өс түбәһе барлыҡҡа килтергән өсмөйөштөң центроиды менән тоташтырыусы дүрт киҫек, дүртмөйөштөң центроидында киҫешәләр һәм киҫешеү нөктәһендә, түбәнән иҫәпләгәндә, 3:1 сағыштырмаһында бүленәләр.
- Шулай уҡ дүртмөйөш центроиды үҙсәнлектәрен ҡарағыҙ.
Дүртмөйөш эсендәге өсмөйөштәрҙең туғыҙ нөктәһе әйләнәләре[үҙгәртергә | сығанаҡты үҙгәртеү]
Ирекле ҡабарынҡы дүртмөйөшөндә уны ике диагонале бүлгән өсмөйөштәренең туғыҙ нөктә әйләнәләре, бер нөктәлә киҫешәләр [5].
Дүртмөйөштәрҙең айырым осраҡтары[үҙгәртергә | сығанаҡты үҙгәртеү]
Әйләнәгә ҡамалған дүртмөйөштәр[үҙгәртергә | сығанаҡты үҙгәртеү]
- Әгәр дүртмөйөш тирәләй әйләнә ҡамап булһа, ул саҡта дүртмөйөш был әйләнәгә ҡамалған тип әйтәләр, һәм киреһенсә.
- Дүртмөйөш тирәләй әйләнә ҡамап була шул саҡта һәм тик шул саҡта ғына, әгәр ҡаршы ятҡан мөйөштәренең суммаһы 180°-ҡа тигеҙ булһа, йәғни:
- .
- Птолемейҙың ике теоремаһы. Ҡаршы ятҡан яҡтары парҙары: a һәм c, b һәм d, шулай уҡ диагоналдәре оҙонлоҡтары e һәм f булған, әйләнәгә ҡамалған ябай (үҙ-үҙе менән киҫешмәүсе) дүртмөйөш өсөн, дөрөҫ:
1) Птолемейҙың беренсе теоремаһы:
- ;
2) Птолемейҙың икенсе теоремаһы: Һуңғы формулала числителдәге a һәм d, b һәм c эргәләш яҡтар парҙары үҙҙәренең остары менән e оҙонлоғондағы диагоналгә таяналар. Ошоға оҡшаш раҫлау знаменатель өсөн дә дөрөҫ. 3) Диагоналдәре оҙонлоҡтары өсөн формулалар (Птолемейҙың беренсе һәм икенсе теоремаларынан эҙемтәләр):
- и
- Әгәр ҡабарынҡы дүртмөйөш әйләнәгә ҡамалған булһа, ул саҡта дүртмөйөштө уның теләһә ниндәй диагонале бүлгән өсмөйөштәр пары ла ошо уҡ әйләнәгә ҡамалған (өсмөйөш әйләнәләре менән бәйләнеш).
- Һуңғы раҫлауҙан килеп сыға: әгәр ҡабарынҡы дүртмөйөштөң яҡтарына үткәрелгән дүрт медиатрисаларҙың (йәки урта перпендикулярҙарҙың) өсәүһе бер нөктәлә киҫешһә, ул саҡта уның дүртенсе яғының медиатрисаһы ла шул уҡ нөктәлә киҫешә. Улай ғына түгел, бындай дүртмөйөш үҙәге күрһәтелгән медиатрисалар киҫешкән нөктәлә булған әйләнәгә ҡамалған [6].

- Бирелгән дүрт Микель тура һыҙыҡтары менән яһалған ҡабарынҡы дүртмөйөш (уңдағы һүрәтте ҡара), әйләнәгә ҡамалған шул саҡта һәм тик шул саҡта ғына, әгәр дүртмөйөштөң Микель нөктәһе M тура һыҙыҡтарҙың алты киҫешеү нөктәһенең икеһен тоташтырған тура һыҙыҡта ятһа (дүртмөйөштөң түбәләре булмаған нөктәләр). Йәғни, әгәр M EF-та ятһа.
- Өсмөйөштөң яғына антипараллель булған һәм уны киҫеп үткән тура һыҙыҡ унан, һәр ваҡытта ла уны ҡамаусы әйләнәһе булған дүртмөйөш киҫеп ала.
- Әйләнәгә ҡамалған дүртмөйөш майҙаны:
- Әйләнәгә ҡамалған дүртмөйөштөң майҙаны Брахмагупта формулаһы буйынса тигеҙ[7]:
- бында p — дүртмөйөштөң ярымпериметры.
- Һуңғы формула «Майҙан» параграфында ҡыҫандағы дөйөм (1) формуланан, унда булыуын иҫәпкә алғанда килеп сыға
- Һуңғы формула Герон формулаһын дүртмөйөш осрағына дөйөмләштереү ул.
- Әйләнәгә ҡамалған дүртмөйөш майҙаны өсөн Брахмагупта формулаһы билдәләүсе аша яҙылырға мөмкин [6]:
- Һуңғы формуланан d=0 булғанда автоматик рәүештә Герон формулаһы өсөн Дроздов В. формулаһы килеп сыға [8][9]:
- Дүртмөйөштө ҡамаусы әйләнә радиусы:

- Теорема[10]. Әгәр әйләнәгә ҡамалған дүртмөйөштә диагональ үткәрһәң, ә барлыҡҡа килгән ике өсмөйөшкә ике әйләнә ҡамаһаң, артабан икенсе диагоналде үткәреп оҡшаш рәүештә эшләһәң, ул саҡта барлыҡҡа килгән дүрт әйләнәнең үҙәктәре тура дүртмөйөштөң түбәләре булалар (йәғни бер әйләнәлә яталар). Был теореманы япон теоремаһы тип атайҙар (Japanese theorem). (һүрәтте ҡарағыҙ). Бынан тыш, дүрт ҡамаусы өсмөйөштәрҙең ортоүҙәктәре бирелгән ABCD дүртмөйөшөнә оҡшаш дүртмөйөштөң түбәләре булып торалар (йәғни башҡа бер әйләнәлә яталар, сөнки бирелгән ҡамалған дүртмөйөштөң түбәләре ниндәйҙер әйләнәлә яталар). Аҙаҡ килеп, был дүрт өсмөйөштөң центроидтары өсөнсө әйләнәлә яталар[11].
- Теорема [12]. — ҡамалған дүртмөйөш булһын, ти. — түбәһенән диагоналенә төшөрөлгән перпендикулярҙың нигеҙе; оҡшаш рәүештә нөктәләре табыла. Ул саҡта нөктәләре бер әйләнәлә яталар.
- Бер яҡтары тигеҙ булған ике өсмөйөштө бергә ҡушҡанда әйләнәгә ҡамалған дүртмөйөш килеп сығыу шарты[13]. Яҡтарының оҙонлоҡтары ярашлы рәүештә (a, b, f) һәм (c, d, f) булған ике өсмөйөш, оҙонлоғо f-кә тигеҙ булған уртаҡ яғы буйынса бергә ҡушҡанда, һөҙөмтәлә яҡтары эҙмә-эҙлекле (a, b, c, d) булған әйләнәгә ҡамалған дүртмөйөшкилеп сыҡһын өсөн, кәрәкле шарт[14]
- Һуңғы шарт әйләнәгә ҡамалған дүртмөйөштөң f диагонале өсөн уның дүрт яғының (a, b, c, d) оҙонлоҡтары аша күрһәткән аңлатма бирә. Был формула Птолемейҙың беренсе һәм икенсе теоремалары асылын күрһәткән формулаларҙы ҡабатлағанда һәм уң һәм һул яҡтарын бер-береһенә тигеҙләгәндә килеп сыға (юғарыла ҡарағыҙ).
- Әйләнәгә ҡамалған дүртмөйөштәрҙең айырым осраҡтары: тура дүртмөйөш, квадрат,тигеҙ эргәле йәки тигеҙ ҡабырғалы трапеция, антипараллелограмм.
- Әйләнәгә ҡамалған дүртмөйөштәр тураһында ентекләберәк «Ҡамалған дүртмөйөш» мәҡәләһендә уҡырға мөмкин.
Әйләнәгә ҡамалған диагоналдәре перпендикуляр булған дүртмөйөштәр (ҡамалған ортодиагоналле дүртмөйөштәр)[үҙгәртергә | сығанаҡты үҙгәртеү]

- Ҡамалған ортодиагоналле дүртмөйөштәр өсөн Брахмагупта теоремаһы дөрөҫ:
Әгәр ҡамалған дүртмөйөштөң нөктәһендә киҫешеүсе диагоналдәре перпендикуляр булһа, ул саҡта уның ике пар антимедиатрисаһы нөктәһе аша үтә.
Иҫкәртеү. Был теоремала антимедиатриса тип [15] һүрәттә уңдағы дүртмөйөштөң киҫеген аңлайҙар (өсмөйөштөң яғына урта перпендикулярға (медиатриса) оҡшаш рәүештә). Ул дүртмөйөштөң бер яғына перпендикуляр һәм бер үк ваҡытта уға ҡаршы ятыусы яғының уртаһы аша үтә.
- Шундай теорема билдәле: Әгәр дүртмөйөштөң диагоналдәре перпендикуляр булһа, ул саҡта һигеҙ нөктә бер әйләнәлә ята (дүртмөйөштөң һигеҙ нөктәһе әйләнәһе): яҡтарының урталары һәм яҡтарының урталарының ҡаршы ятыусы яҡтарына проекциялары [16]. Ошо теореманан һәм Брахмагупта теоремаһынан, ҡамалған ортодиагоналле дүртмөйөштөң ике пар антимедиатрисаларының остары (һигеҙ нөктә) бер әйләнәлә ятыуы килеп сыға (дүртмөйөштөң һигеҙ нөктәһе әйләнәһе).
- Квадрат әйләнәгә ҡамалған ортодиагоналле дүртмөйөштөң айырым осрағы булып тора.
Әйләнәне ҡамаусы дүртмөйөштәр[үҙгәртергә | сығанаҡты үҙгәртеү]
- Әгәр дүртмөйөшкә әйләнә ҡамап булһа, ул саҡта дүртмөйөш был әйләнәне ҡамаусы була тип әйтәләр, һәм киреһенсә.
- Ҡайһы бер (ләкин бөтәһе лә түгел) дүртмөйөштәргә әйләнә ҡамап була. Улар ҡамаусы дүртмөйөштәр тип аталалар. Бындай дүртмөйөштәрҙең иң мөһим үҙсәнлектәренең береһе булып, ҡаршы ятҡан яҡтарының оҙонлоҡтары суммалары тигеҙ булыуы тора. Был раҫлау Пито теоремаһы тип атала.
- Икенсе төрлө әйткәндә, ҡабарынҡы дүртмөйөш әйләнәне ҡамаусы була шул саҡта һәм тик шул саҡта ғына, әгәр ҡаршы ятыусы яҡтарының оҙонлоҡтары суммаһы тигеҙ булһа, йәғни: .
- Ҡамалған әйләнәнең дүртмөйөш менән тейеү нөктәләре дүртмөйөштөң мөйөштәренән тигеҙ киҫектәр киҫеп ала.
- Ҡамаусы дүртмөйөштөң майҙаны
- шарты тигәнде аңлата.
Ярымпериметр p төшөнсәһе индереп, , булыуын табабыҙ. Артабан булыуын күрергә була. Ошонан сығып, Ул саҡта «Майҙан» параграфындағы (1) формула буйынса табабыҙ
- Дүртмөйөш ҡамаусы булғанлыҡтан, уның майҙаны ярымпериметр p менән ҡамалған әйләнә радиусы r ҡабатландығына тигеҙ: .
- Әгәр ҡабарынҡы дүртмөйөш — трапеция ла һәм параллелограмм да булмаһа һәм ниндәйҙер әйләнәне ҡамаусы булһа, ул саҡта ошо уҡ әйләнәне ҡамаусы ике өсмөйөш бар, улар дүртмөйөштөң ҡаршы ятыусы яҡтары парҙарын киҫешкәнгә тиклем дауам иткәндә барлыҡҡа килә (өсмөйөш әйләнәләре менән бәйләнеш).
- Һуңғы раҫлаҙан килеп сыға: әгәр ҡабарынҡы дүртмөйөштөң эске мөйөштәренең дүрт биссектрисаһының (йәки биссекторҙарының) өсәүһе бер нөктәлә киҫешһә, ул саҡта уның дүртенсе эске мөйөшөнөң биссектрисаһы ла шул уҡ нөктәлә киҫешә. Улай ғына түгел, бындай дүртмөйөш үҙәге ошо биссектрисалар киҫешкән нөктәлә булған ниндәйҙер әйләнәне ҡамаусы була[17].
- Әгәр дүртмөйөш әйләнәне ҡамаусы булһа, ул саҡта ҡамалған әйләнәнең үҙәге Ньютон тура һыҙығында ята. Анығыраҡ раҫлау түбәндә.
- Һәр ҡамаусы дүртмөйөштә ике диагоналдең уртаһы һәм ҡамалған әйләнәнең үҙәге бер тура һыҙыҡта яталар (Ньютон теоремаһы). Остары дүртмөйөштөң ҡаршы ятыусы яҡтарының дауамдары киҫешкән нөктәләрҙә булған (әгәр улар параллель булмаһа) киҫектең уртаһы ла шул уҡ тура һыҙыҡта ята. Был тура һыҙыҡ Гаусс тура һыҙығы тип атала. Һүрәттә (өҫтә икенсе төркөм һүрәттәр) ул йәшел төҫтә, диагоналдәре ҡыҙыл, остары дүртмөйөштөң ҡаршы ятыусы яҡтарының дауамдары киҫешкән нөктәләрҙә булған киҫек тә ҡыҙыл төҫтә.
- Дүртмөйөштө ҡамаусы әйләнәнең үҙәге — түбәләре диагоналдәрҙең киҫешеү нөктәһендә һәм ҡаршы ятыусы яҡтарының дауамдары киҫешкән нөктәләрҙә булған өсмөйөштөң бейеклектәре киҫешкән нөктә (Брокар теоремаһы).
- Әйләнәне ҡамаусы дүртмөйөштәрҙең айырым осраҡтары булып торалар: ромб, квадрат, дельтоид.
Ҡамалған-ҡамаусы дүртмөйөш[үҙгәртергә | сығанаҡты үҙгәртеү]

Ҡамалған-ҡамаусы дүртмөйөштәр — бер үк ваҡытта ниндәйҙер әйләнәне ҡамаусы, шулай уҡ ниндәйҙер әйләнәгә ҡамалған дүртмөйөштәр. Уларҙың икенсе төрлө атамалары — бицентрик дүртмөйөштәр (Bicentric quadrilateral), хорда-тейеүсе дүртмөйөштәр (chord-tangent quadrilateral) йәки ике-әйләнәле дүртмөйөштәр (double circle quadrilateral) [18].
Үҙсәнлектәре[үҙгәртергә | сығанаҡты үҙгәртеү]
- Түбәндә күрһәтелгән ике шарттың һәр береһе айырым алғанда, бирелгән дүртмөйөш ниндәйҙер әйләнәләр өсөн ҡамалған-ҡамаусы булһын өсөн кәрәкле, ләкин етерлек шарт түгел:
и .
- Һуңғы ике шарттың бер үк ваҡытта үтәлеүе ниндәйҙер ҡабарынҡы дүртмөйөш өсөн, был дүртмөйөш ҡамалған-ҡамаусы булһын өсөн кәрәкле һәм етерлек шарт була.
- Ҡамалған-ҡамаусы дүртмөйөштөң майҙаны:
- Әгәр дүртмөйөш ҡамалған да һәм ҡамаусы ла булһа, ул саҡта «Майҙан» параграфы сиктәрендә (1) формула буйынса: .
- Һуңғы формула алдағы параграфтың ҡамаусы дүртмөйөш майҙаны өсөн формулаһынан , булыуын иҫәпкә алып килеп сыға (ҡамалған дүртмөйөш өсөн ).
- Дүртмөйөш ҡамаусы булғанлыҡтан, уның майҙаны шулай уҡ уның ярымпериметры p менән ҡамалған әйләнә радиусы r ҡабатландығына тигеҙ: .
- Ҡамалған-ҡамаусы дүртмөйөштөң майҙаны өсөн икенсе формула:
- Фусс теоремаһы (Fuss' theorem) [19].

Бирелгән дүртмөйөштөң ярашлы рәүештә ҡамаусы һәм ҡамалған әйләнә радиустары R һәм r һәм был әйләнәләрҙең үҙәктәре һәм араһындағы алыҫлыҡ x өсөн (см. рис.) дүртмөйөшлө аналогты сағылдырыусы нисбәт үтәлә Эйлер теоремаһы (өсмөйөш өсөн оҡшаш Эйлер формулаһы бар)[20][21][22]:
йәки
йәки
йәки

- Ҡамалған-ҡамаусы дүртмөйөш өсөн артабанғы өс шарт тейеүсе дүртмөйөшкә ҡамалған әйләнәнең яҡтарына тейеү нөктәләренә ҡағыла. Әгәр ҡамалған әйләнә AB, BC, CD, DA яҡтарына ярашлы рәүештә W, X, Y, Z нөктәләрендә тейһә, ул саҡта ABCD тейеүсе дүртмөйөшө лә шулай уҡ ҡамаусы була, әгәр артабанғы өс шарттың һәр береһе үтәлһә генә (һүрәтте ҡарағыҙ):[23]
- WY XZ-ҡа перпендикуляр
- .
- Квадрат ҡамалған-ҡамаусы дүртмөйөштөң айырым осрағы булып тора.
Яҡтары перпендикуляр булған дүртмөйөштәр[үҙгәртергә | сығанаҡты үҙгәртеү]
- Дүртмөйөштөң ике ҡаршы ятыусы яҡтары перпендикуляр шул саҡта һәм тик шул саҡта ғына, әгәр ҡалған ике ҡаршы ятыусы яҡтарының квадраттары суммаһы диагоналдәре квадраттары суммаһына тигеҙ булһа.
- Әгәр ҡабарынҡы дүртмөйөштөң ике пар эргәләш яҡтары перпендикуляр булһа (йәғни ике ҡаршы ятыусы мөйөштәре тура булһа), ул саҡта был дүртмөйөш ниндәйҙер әйләнәгә ҡамалған булырға мөмкин. Улай ғына түгел, һүҙ барған ике пар эргәләш яҡтары үҙҙәренең бер остары менән таянған диагональ был әйләнәнең диаметры булып хеҙмәт итә.
- Яҡтары перпендикуляр булған дүртмөйөштәрҙең айырым осраҡтары булып торалар: тура дүртмөйөш һәм квадрат.
Диагоналдәре перпендикуляр булған дүртмөйөштәр[үҙгәртергә | сығанаҡты үҙгәртеү]
- Диагоналдәре перпендикуляр булған дүртмөйөштәр ортодиагоналле дүртмөйөштәр тип аталалар.
- Дүртмөйөштөң диагоналдәре перпендикуляр була шул саҡта һәм тик шул саҡта ғына, әгәр ҡаршы ятыусы яҡтарының квадраттары суммаһы тигеҙ булһа.
- Ортодиагоналле дүртмөйөштөң майҙаны уның диагоналдәре ҡабатландығының яртыһына тигеҙ: .
- Дүртмөйөштөң урта һыҙыҡтары тигеҙ шул саҡта һәм тик шул саҡта ғына, әгәр ҡаршы ятыусы яҡтарының квадраттары суммаһы тигеҙ булһа.
- Дүртмөйөштөң антимедиатрисаһы тип уның бер яғының уртаһынан сығып ҡаршы ятыусы яғына перпендикуляр булған тура һыҙыҡ киҫеге атала.
- Брахмагупта теоремаһы. Әгәр дүртмөйөштөң диагоналдәре перпендикуляр һәм ул ниндәйҙер әйләнәгә ҡамалған булһа, ул саҡта уның дүрт антимедиатрисаһы бер нөктәлә киҫешә. Улай ғына түгел, был антимедиатрисаларҙың киҫешеү нөктәһе уның диагоналдәренең киҫешеү нөктәһе булып тора.
- Әгәр дүртмөйөштөң диагоналдәре перпендикуляр һәм ул ниндәйҙер әйләнәгә ҡамалған булһа, ул саҡта учетверенный её уның R радиусының дүртләтелгән квадраты теләһә ниндәй ҡаршы ятыусы яҡтар парының квадраттары суммаһына тигеҙ:
- Әгәр дүртмөйөштөң диагоналдәре перпендикуляр һәм ул ниндәйҙер әйләнәне ҡамаусы булһа, ул саҡта уның ике пар ҡаршы ятыусы яҡтары ҡабатландығы тигеҙ:
- Түбәләре ортодиагоналле дүртмөйөштөң яҡтарының уртаһында булған Вариньон параллелограмы тура дүртмөйөш була.
- Әгәр дүртмөйөштөң диагоналдәре перпендикуляр булһа, ул саҡта һигеҙ нөктә: яҡтарының урталары һәм яҡтарының урталарының ҡаршы ятыусы яҡтарына проекциялары бер әйләнәлә (дүртмөйөштөң һигеҙ нөктәһе әйләнәһе) яталар [16].
- Частными Ортодиагоналле дүртмөйөштәрҙең айырым осраҡтары булып торалар: ромб, квадрат, дельтоид.
- Әгәр ҡабарынҡы дүртмөйөштөң диагоналдәре перпендикуляр булһа, ул саҡта уның дүрт яғының урталары тура дүртмөйөш түбәләре була (Вариньон теоремаһы эҙемтәһе). Кире теорема ла дөрөҫ. Бынан тыш, тура дүртмөйөштөң диагоналдәре тигеҙ. Ошонан сығып, ҡабарынҡы дүртмөйөштөң диагоналдәре перпендикуляр була шул саҡта һәм тик шул саҡта ғына, әгәр уның ике бимедианаларының (ҡаршы ятыусы яҡтарының урталарын тоташтырыусы киҫектәр) оҙонлоҡтары үҙ-ара тигеҙ булһа[24].
- Ҡамаусы һәм ортодиагоналле дүртмөйөштәрҙең үҙсәнлектәрен сағыштырыу таблицаһы:
Уларҙың оҙонлоҡ үҙсәнлектәре бик оҡшаш (таблицаны ҡарағыҙ)[24] Бында тамғалауҙар: a, b, c, d — уларҙың яҡтары оҙонлоҡтары, R1, R2, R3, R4 - был яҡтар һәм диагоналдәренең киҫешеү нөктәһе аша үтеүсе әйләнәләрҙең радиустары, h1, h2, h3, h4 — диагоналдәренең киҫешеү нөктәһенән яҡтарына төшөрөлгән бейеклектәр.
| ҡамаусы дүртмөйөш | ортодиагоналле дүртмөйөш |
|---|---|
- Бынан тыш, ортодиагоналле дүртмөйөштөң диагоналдәренең киҫешеү нөктәһенән яҡтарына төшөрөлгән медианалар өсөн, дөрөҫ: .
Тыштан ҡамаусы дүртмөйөш[үҙгәртергә | сығанаҡты үҙгәртеү]
- Тыштан ҡамаусы дүртмөйөш — бөтә дүрт яғының дауамы әйләнәгә тейеүсе булған ҡабарынҡы дүртмөйөш ул (дүртмөйөштән тышта)[25]. Әйләнә тыштан ҡамалған тип атала. Тыштан ҡамалған әйләнәнең үҙәге алты биссектрисаның киҫешеү нөктәһе булып тора.
- Иҫкәртеү. Ҡамалған, ҡамаусы, шулай уҡ тыштан ҡамалған әйләнәләрҙе теләһә ниндәй дүртмөйөштә үткәреп булмай. Әгәр ABCD ҡабарынҡы дүртмөйөшөнөң ҡаршы ятыусы яҡтары E һәм F нөктәләрендә киҫешһә, уның тыштан ҡамалған булыуы шарты булып түбәндәге ике шарттың теләһә ҡайһыһы тора:
Ҡайһы бер дүртмөйөштәрҙең диагоналдәре үҙсәнлектәре[үҙгәртергә | сығанаҡты үҙгәртеү]
Түбәндәге таблицала, ҡайһы бер иң төп дүртмөйөштәрҙең диагоналдәре киҫешеү нөктәләрендә урталай киҫешәләрме, диагоналдәре перпендикулярмы, диагоналдәре тигеҙме, һәм диагоналдәре мөйөштәрен урталай бүләме икәнлеге күрһәтелгән.[26] Исемлек дөйөм осраҡтарға ҡағыла, һәм дүртмөйөштәрҙең аталған аҫкүмәклектәрен ҡарап сыға.
| Дүртмөйөш | Диагоналдәренең киҫешеү нөктәһендә урталай бүленеүе | Диагоналдәренең перпендикулярлеге | Диагоналдәре оҙонлоҡтарының тигеҙлеге | Мөйөштәренең диагоналдәре менән урталай бүленеүе |
|---|---|---|---|---|
| Трапеция | Юҡ | 1-се иҫкәртеүҙе ҡарағыҙ | Юҡ | Юҡ |
| Равнобедренная трапеция | Юҡ | См. замечание 1 | Эйе | Ике ҡаршы ятыусы мөйөштәренең булһа ла |
| Параллелограмм | Эйе | Юҡ | Юҡ | Юҡ |
| Дельтоид | 2-се иҫкәртеүҙе ҡарағыҙ | Эйе | 2-се иҫкәртеүҙе ҡарағыҙ | 2-се иҫкәртеүҙе ҡарағыҙ |
| Прямоугольник | Эйе | Юҡ | Эйе | Юҡ |
| Ромб | Эйе | Эйе | Юҡ | Эйе |
| Квадрат | Эйе | Эйе | Эйе | Эйе |
Иҫкәртеү 1: Трапецияларҙың дөйөм алғанда һәм тигеҙ эргәле трапецияларҙың перпендикуляр диагоналдәре юҡ, ләкин сикһеҙ күп һанда (оҡшаш булмаған) трапециялар һәм тигеҙ эргәле трапециялар бар, уларҙың ысынлап та диагоналдәре перпендикуляр һәм улар ниндәй ҙә булһа башҡа аталған дүртмөйөшкә оҡшамаған.
Иҫкәртеү 2: Дельтоидтың бер диагонале икенсеһен урталай бүлә. Икенсе диагонале уның ҡаршы ятыусы мөйөштәрен урталай бүлә. Дөйөм дельтоидтың диагоналдәре тигеҙ түгел, ләкин сикһеҙ күп һанда (оҡшаш булмаған) дельтоидтар бар, уларҙың диагоналдәре нең оҙонлоҡтары тигеҙ (һәм дельтоидтар ниндәй ҙә булһа башҡа аталған дүртмөйөш түгелдәр).
Майҙан[үҙгәртергә | сығанаҡты үҙгәртеү]
- Ирекле үҙ-үҙе менән киҫешмәүсе, яҫылыҡта үҙенең түбәләренең координаталары менән бирелгән дүртмөйөштөң майҙаны тигеҙ:
- Ирекле үҙ-үҙе менән киҫешмәүсе, диагоналдәре , һәм улар (йәки уларҙың дауамы) араһындағы мөйөшө булған ҡабарынҡы дүртмөйөштөң майҙаны тигеҙ:
- Ирекле ҡабарынҡы дүртмөйөштөң майҙаны дүртмөйөштөң беренсе һәм икенсе урта һыҙыҡтарының улар араһындағы мөйөшө синусына ҡабатландығына тигеҙ, йәғни
- .
Иҫкәртеү. Дүртмөйөштөң беренсе һәм икенсе урта һыҙыҡтары — ҡаршы ятҡан яҡтарының урталарын тоташтырыусы киҫектәр.
- , бында , — диагоналдәре оҙонлоҡтары, a, b, c, d — яҡтары оҙонлоҡтары.
- Ирекле ҡабарынҡы дүртмөйөштөң майҙаны шулай уҡ тигеҙ
|
(1) |
бында p — ярымпериметр, ә дүртмөйөштөң ҡаршы ятыусы мөйөштәренең ярымсуммаһы (Ҡайһы ҡаршы ятыусы мөйөштәре парын алыуҙың әһәмиәте юҡ, сөнки бер пар ҡаршы ятыусы мөйөштәре ярымсуммаһы тигеҙ булһа, ул саҡта икенсе пар ҡаршы ятыусы мөйөштәре ярымсуммаһы була һәм ). Ошо формуланан ҡамалған дүртмөйөштәр өсөн Брахмагупта формулаһы килеп сыға.
- Ирекле ҡабарынҡы дүртмөйөштөң майҙаны (1) формула буйынса Бретшнайдер нисбәттәренең береһен иҫәпкә алып (юғарыла ҡарағыҙ) ошондай күренештә яҙылырға мөмкин:
бында p — ярымпериметр, e һәм f -дүртмөйөштөң диагоналдәре.
Тарихы[үҙгәртергә | сығанаҡты үҙгәртеү]
Борон египетлылар һәм башҡа ҡайһы бер халыҡтар дүртмөйөштөң майҙанын табыу өсөн дөрөҫ булмаған формуланы ҡулланғандар — уның a, b, c, d ҡаршы ятыусы яҡтары ярымсуммаһы ҡабатландығын [27]:
- .
Тура мөйөшлө булмаған дүртмөйөштәр өсөн был формула майҙандың артығыраҡ ҡиммәтен бирә. Был формула тура мөйөшлө тиерлек ер участкалары майҙанын иҫәпләү өсөн генә ҡулланылған тип фараз итергә була. Тура дүртмөйөштөң яҡтарын теүәл үлсәмәгәндә, был формула бирелгән үлсәмдәрҙе уртасалау иҫәбенә һөҙөмтәне яҡшыртырға мөмкинлек бирә.
Шулай уҡ ҡарағыҙ[үҙгәртергә | сығанаҡты үҙгәртеү]
- Планиметрия глоссарий
- категория «Әйләнәләр»
- Алтынсы әйләнә тураһында лемма
- Птолемей тигеҙһеҙлеге
- Әйләнә
- Гаусс тура һыҙығы
- Обер тура һыҙығы
- Вариньон параллелограммы
- Тебо теоремаһы 1
- Бретшнайдер нисбәте
- Кейси теоремаһы
- Дүртмөйөш өсөн косинустар теоремаһы
- Ньютон теоремаһы (планиметрия)
- Күбәләк тураһында теорема
- Птолемей теоремаһы
- Микель нөктәһе
- Өсмөйөш
- Ҡамалған дүртмөйөш
Иҫкәрмәләр[үҙгәртергә | сығанаҡты үҙгәртеү]
- ↑ Стариков, 2016, с. 95-97
- ↑ 2,0 2,1 Четырёхугольники.
- ↑ E.W. Weisstein. Bimedian. MathWorld – A Wolfram Web Resource.
- ↑ 4,0 4,1 Четырёхугольник. Специальные отрезки прямых (Quadrilateral, Special line segments. (англ. яз.))
- ↑ Заславский, Пермякова и др., 2009, с. 118, задача 9
- ↑ 6,0 6,1 Стариков, 2014, с. 38, правая колонка, пункт 7
- ↑ 7,0 7,1 Понарин, с. 74
- ↑ Дроздов, 1995, с. обложка
- ↑ Мухлаев, 2006, с. 8
- ↑ Ayeme, с. 6, Упр. 8, рис. 13
- ↑ Andreescu, Titu & Enescu, Bogdan (2004), "2.3 Cyclic quads", «Mathematical Olympiad Treasures», Springer, сс. 44–46, 50, ISBN 978-0-8176-4305-8
- ↑ Ayeme, с. 5, Упр. 7, рис. 11, следствие
- ↑ См. подраздел «Диагонали» статьи «Вписанный четырёхугольник»
- ↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ. Co., 2007
- ↑ Стариков, 2014, с. 7-39
- ↑ 16,0 16,1 Заславский, Пермякова и др., 2009, с. 118, задача 11
- ↑ Стариков, 2014, с. 39, левая колонка, последний абзац
- ↑ Вписано-описанные четырёхугольники (Bicentric quadrilateral. англ. яз.// https://en.wikipedia.org/wiki/Bicentric_quadrilateral#Fuss.27_theorem)
- ↑ Вписано-описанный четырёхугольник (Bicentric quadrilateral. англ. яз.// https://en.wikipedia.org/wiki/Bicentric_quadrilateral#Fuss.27_theorem)
- ↑ Dörrie Heinrich. 100 Great Problems of Elementary Mathematics: Their History and Solutions. — New York: Dover. — P. 188–193. — ISBN 978-0-486-61348-2.
- ↑ Yiu, Paul, Euclidean Geometry, [1](недоступная ссылка), 1998, pp. 158—164.
- ↑ Salazar, Juan Carlos (2006), "«Fuss's Theorem»", Mathematical Gazette Т. 90 (July): 306–307.
- ↑ Josefsson, Martin (2010), "«Characterizations of Bicentric Quadrilaterals»", Forum Geometricorum Т. 10: 165–173, <http://forumgeom.fau.edu/FG2010volume10/FG201019.pdf>.
- ↑ 24,0 24,1 Josefsson, Martin (2012), "«Characterizations of Orthodiagonal Quadrilaterals»", Forum Geometricorum Т. 12: 13–25, <http://forumgeom.fau.edu/FG2012volume12/FG201202.pdf>.
- ↑ Radic, Kaliman, Kadum, 2007, с. 33—52
- ↑ Jennifer Kahle, Geometry: Basic ideas (англ. яз.).Геометрия: Основные идеи [2], accessed 28 December 2012.
- ↑ Г. Г. Цейтен История математики в древности и в средние века, ГТТИ, М-Л, 1932.
Әҙәбиәт[үҙгәртергә | сығанаҡты үҙгәртеү]
- Болтянский В., Четырёхугольники. Квант, № 9,1974.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 74. — ISBN 5-94057-170-0.
- Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). // Научный журнал Globus'. — С-П., 2016.
- Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. / Гл. ред. Романова И. В.. — Чебоксары: ЦДИП «INet», 2014. — В. 1.
- Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду / Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова.. — Москва: МЦНМО, 2009. — ISBN 978-5-94057-477-4.
- Jean-Louis Ayeme. Feurbach’s theorem. A new purely synthetic proof. 2013 йыл 13 ноябрь архивланған. Несколько расширенный перевод — «Вокруг задачи Архимеда»
- Дроздов В. Геронов определитель. Занимательная страница // Математика в школе. — 1995. — В. 5.
- Мухлаев А. 38–я открытая областная научная конференция учащихся. — Омск, 2006.
- Mirko Radic, Zoran Kaliman, Vladimir Kadum A condition that a tangential quadrilateral is also a chordal one // Mathematical Communications. — 2007. — В. 12.
- D. Fraivert, A. Sigler and M. Stupel Common properties of trapezoids and convex quadrilaterals // Journal of Mathematical Sciences: Advances and Applications. — 2016. — Т. 38. — P. 49–71. — DOI:10.18642/jmsaa_7100121635
Был мәҡәләгә түбәндәгеләр етешмәй. Ошоларҙы төҙәтеп йә өҫтәп, һеҙ уны яҡшырта алаһығыҙ?: |
Ряд коротких примечаний не содержится в статье или не ведёт на раздел «Литература». |
[[Категория:{| align="right"
































































































