Параллеллек
Параллеллек — тура һыҙыҡтар араһындағы бәйләнеш.
Төрлө геометрия бүлектәрендә төрлөсәрәк билдәләмә бирелә.
Евклид геометрияһында
[үҙгәртергә | сығанаҡты үҙгәртеү]Евклид геометрияһында параллель тура һыҙыҡтар тип, бер яҫылыҡта ятҡан һәм киҫешмәүсе тура һыҙыҡтар атала.
һәм тура һыҙыҡтарының параллеллеге ғәҙәттә тип тамғалана.
Үҙсәнлектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]- Параллеллек — бинар эквивалентлылыҡ бәйләнеше, шуға күрә бөтә тура һыҙыҡтар күмәклеген үҙ-ара параллель тура һыҙыҡтар кластарына бүлә.
- Теләһә ниндәй нөктә аша бирелгән тура һыҙыҡҡа параллель булған бер генә тура һыҙыҡ үткәрергә мөмкин. Был Евклид геометрияһының мөһим, үҙенә генә хас үҙенсәлеге, башҡа геометрияларҙа 1 һаны икенсе һандар менән алмаштырылған (Лобачевский геометрияһында бындай тура һыҙыҡтар сикһеҙ күп, улар ике ситке тура һыҙыҡтар менән сикләнгән тура һыҙыҡтар шәлкемен барлыҡҡа килтерә).
- Арауыҡта 2 параллель тура һыҙыҡ бер яҫылыҡта ята.
- 2 параллель тура һыҙыҡты өсөнсөһө, киҫеүсе тип аталған тура һыҙыҡ киҫкәндә:
- Киҫеүсе ике тура һыҙыҡты ла киҫеп үтә.
- Киҫелештә 8 мөйөш барлыҡҡа килә, ҡайһы бер характерлы парҙары айырым исемдәр менән атала һәм үҙсәнлектәргә эйә:
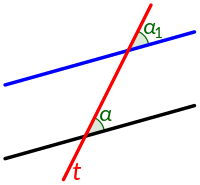
- Арҡыры ятыусы мөйөштәр тигеҙ (һүрәтте ҡарағыҙ).
- Ярашлы мөйөштәр тигеҙ (һүрәтте ҡарағыҙ).
- Бер яҡлы мөйөштәрҙең суммаһы 180°-ҡа тигеҙ (дөрөҫөрәге, эске арҡыры ятыусы булмаған мөйөштәр[1], һүрәтте ҡарағыҙ).
Лобачевский геометрияһында
[үҙгәртергә | сығанаҡты үҙгәртеү]
Лобачевский геометрияһында яҫылыҡта тура һыҙығынан ситтә ятҡан нөктәһе аша -ны киҫеп үтмәгән сикһеҙ күп тура һыҙыҡ үтә. тура һыҙығы тура һыҙығына -нан -ға ҡарай йүнәлештә равнобежная тура һыҙыҡ тип атала, әгәр:
- һәм нөктәләре тура һыҙығынан бер яҡта ятһа;
- тура һыҙығы тура һыҙығын киҫеп үтмәй, әммә мөйөшөнөң эсендә ятҡан һәр нур нурын киҫеп үтә.
Аналогично определяется прямая, равнобежная тура һыҙығына -нан -ға ҡарай йүнәлештә равнобежная тура һыҙыҡҡа билдәләмә оҡшаш рәүештә бирелә.
Равнобежные тура һыҙыҡтар шулай уҡ асимптотик параллель йәки параллель тип кенә аталалар. Бирелгән тура һыҙыҡты киҫеп үтмәүсе башҡа бөтә тура һыҙыҡтар ультрапараллель йәки таралышыусы тура һыҙыҡтар тип аталалар[2].
Шулай уҡ ҡарағыҙ
[үҙгәртергә | сығанаҡты үҙгәртеү]- Антипараллеллек
- Яҫылыҡтар параллеллеге
- Асамай тура һыҙыҡтар
- Перпендикулярлек
- Ортогоналлек
- Трансверсаль (геометрия)
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ Consecutive Interior Angles (внутренние не накрест лежащие углы)
- ↑ Математический справочник 2016 йыл 23 сентябрь архивланған.
Һылтанмалар
[үҙгәртергә | сығанаҡты үҙгәртеү]- Антипараллельные линии // Брокгауз һәм Ефрондың энциклопедик һүҙлеге: 86 томда (82 т. һәм 4 өҫтәмә том). — СПб., 1890—1907. (рус.)
| Был геометрия буйынса тамамланмаған мәҡәлә. Һеҙ мәҡәләне төҙәтеп һәм тулыландырып проектҡа ярҙам итә алаһығыҙ. |