Евклидтың параллеллек аксиомаһы

Евкли́дтың параллеллек аксиомаһы, йәки бишенсе постула́т — классик планиметрияның нигеҙендә ятҡан аксиомаларҙың береһе. Иң тәүге тапҡыр Евклидтың «Башланғыстарында» килтерелә[1]:
|
Евклид постулат һәм аксиома тигән төшөнсәләрҙе айыра, ләкин уларҙың айырмаһын аңлатып тормай; Евклид «Башланғыстар»ының төрлө манускрипттарында аксиомаларға һәм постулаттарға бүленеш төрлө, уларҙың тәртибе лә тура килмәй. «Башланғыстар»ҙың Йохан Людвиг Гейберг әҙерләп сығарған классик баҫмаһында формалаштырылған ҡағиҙә бишенсе постулат булып тора.
Хәҙерге телдә Евклид тексын ошолай төҙөргә мөмкин[2]:
|
Тап ниндәй яҡтан киҫешәсәктәре тураһындағы аныҡлауҙы Евклид, моғайын, асыҡлыҡ индереү өсөн өҫтәгәндер — уларҙың киҫешәсәктәре фактына бәйлелекте иҫбатлау еңел[2].
Бишенсе постулат Евклидтың ябай һәм интуиция кимәлендә аңлашылып торған башҡа постулаттарынан ныҡ айырыла (ҡара: «Евклидтың башланғыстары»). Шул сәбәпле ике мең йыл буйы уны, аксиомалар исемлегенән сығарып, теорема итергә тырышыуҙар туҡтамай. Бөтә был тырышлыҡтар уңышһыҙлыҡҡа осрап тора. «Моғайын, фәндә Евклидтың бишенсе постулаты тарихынан да мауыҡтырғысыраҡ һәм моңһоуыраҡ тарихты табып та булмайҙыр»[3]. Ыңғай һөҙөмтәһе булмаһа ла, был эҙләнеүҙәр бушҡа үтмәй, сөнки һуңғы сиктә улар барыбер Ғаләм геометрияһы тураһындағы ғилми ҡараштарҙы өр-яңынан ҡарау ихтыяжын тыуҙыра.
Параллель һыҙыҡтар тураһындағы постулаттың эквивалентлы бирелештәре[үҙгәртергә | сығанаҡты үҙгәртеү]
Хәҙерге заман сығанаҡтарында ғәҙәттә параллель һыҙыҡтар тураһындағы постулаттың башҡа төрлө бирелеше килтерелә, ул V постулатҡа эквивалентлы (торошло) һәм Прокл Диадох тарафынан төҙөлгән[4] (сит илдәрҙә уны йыш ҡына Джон Плейфэр аксиомаһы тип атайҙар):

|
Был бирелештә «бер генә һәм тик бер генә» тигән һүҙҙәрҙе йыш ҡына «тик бер генә» йәки «берәүҙән артыҡ булмаған» тигәнгә алмаштыралар, сөнки ошондай бер генә булһа ла параллель һыҙыҡ булыуы Евклид «Башланғыстар»ының 27 һәм 28 теоремаларынан килеп сыға.
Ғүмүмән, V постулаттың эквивалент бирелештәре бик күп, уларҙың күбеһе үҙенән-үҙе дөрөҫ булып күренә. Бына уларҙың ҡайһы берҙәре[5][6][7].
- Тура дүртмөйөш бар икән (берәү булһа ла), тимәк, бөтә мөйөштәре тура булған дүртмөйөш бар[8].
- Оҡшаш, ләкин тигеҙ булмаған өсмөйөштәр бар (Джон Валлис аксиомаһы, 1693). Һәм бында ошондай ике өсмөйөш булыуы ла етә[8].
- Теләһә ниндәй фигураны пропорциональ рәүештә ҙурайтып була.
- Вариант: пропорциональ ҙурайтып була торған кәм тигәндә бер фигура бар.
- Майҙаны теләһә күпме ҙурлыҡта була торған өсмөйөш бар.
- Мөйөш эсендәге нөктә аша үтеүсе тура һыҙыҡ уның кәм тигәндә бер яғын киҫеп үтә (Иоганн Фридрих Лоренц аксиомаһы, 1791).
- Ҡыҫынҡы мөйөш эсендәге һәр нөктә аша уның ике яғын да киҫә торған тура һыҙыҡ үткәреп була (Адриен Мари Лежандр фараздарының береһе, 1800).
- Бер-береһенә яҡынайыусы тура һыҙыҡтар иртәме, һуңмы киҫешәсәк.
- Вариант: бер үк тура һыҙыҡҡа ҡарата перпендикуляр һыҙыҡ менән ауыш һыҙыҡ мотлаҡ киҫешәсәк. Был раҫлау XIII быуатта Насыр ад-Дин Тусиҙа уҡ осраһа ла, Лежандр постулаты булараҡ билдәле.
- Бирелгән тура һыҙыҡтан бер тигеҙ алыҫлыҡта ятыусы нөктәләр (уның бер яғындағылар) тура һыҙыҡ хасил итә.
- Вариант: параллель тура һыҙыҡтар араһындағы алыҫлыҡ һәр ваҡыт даими, йәғни параллель тура һыҙыҡтар яҡынлаша ла, алыҫлаша ла алмай.
- Әгәр ике тура һыҙыҡ бер-береһенә яҡынлаша башлаһа, уларҙың (бер үк яҡҡа, киҫешмәйсә) алыҫлаша башлауы мөмкин түгел (Роберт Симсон аксиомаһы, 1756).
- Вариант: Әгәр ике тура һыҙыҡ бер яҡҡа бер-береһенән алыҫлашһа, икенсе яҡҡа — яҡынлашалар.
- Бөтә өсмөйөштәрҙең дә мөйөштәре суммаһы бер төрлө.
- Вариант: мөйөштәренең суммаһы бер иш булған төрлө ҙурлыҡтағы кәм тигәндә ике өсмөйөш бар.
- Мөйөштәренең суммаһы ике тура мөйөшкә тиң булған (кәм тигәндә бер), өсмөйөш бар[8].
- Ике тура һыҙыҡ өсөнсөһөнә параллель булһа, бер-береһенә лә параллель була (Остроградский аксиомаһы, 1855).
- Ниндәй ҙә булһа параллель һыҙыҡтар тупланмаһына ҡарата ортогональ булған һыҙыҡ тура һыҙыҡ булып тора.
- Параллель һыҙыҡтарҙың береһен киҫкән тура һыҙыҡ икенсеһен дә мотлаҡ киҫәсәк.
- Һәр бер әүерелмәгән өсмөйөш өсөн ҡамаусы әйләнә бар (Фаркаш Бойяи аксиомаһы).
- Пифагор теоремаһы ғәҙел (кәм тигәндә тура мөйөшлө бер өсмөйөштә).
- Вариант: арауыҡ Евклид метрикаһына эйә.
- Әйләнәнең оҙонлоғо менән диаметры нисбәте константа булып тора, йәғни һәр бер әйләнә өсөн бер төрлө.
- Вариант: әйләнә оҙонлоғоноң уның диаметрына нисбәте Пи һанына тиң (бер генә әйләнәнеке булһа ла).
Уларҙың эквивалентлығы шуны аңлата: V постулат аша уларҙың бөтәһен дә иҫбатлап була һәм, киреһенсә, V постулатты ошо формулировкаларҙың ҡайһыһына алмаштырһаҡ та, инеш V постулатты теорема кеүек итеп иҫбатлай алабыҙ.
Әгәр V постулат урынына, нөктә — тура һыҙыҡ пары өсөн V постулат дөрөҫ түгел тип ҡараһаҡ, килеп сыҡҡан аксиомалар системаһы Лобачевский геометрияһын һүрәтләр. Аңлашылыуынса, Лобачевский геометрияһы өсөн үрҙә һаналған эквивалент раҫлауҙар дөрөҫ түгел.
Сферик геометрия аксиомалары системаһы шулай уҡ Евклидтың[9] башҡа аксиомаларын үҙгәртеүҙе лә талап итә.
Бишенсе постулат былай ҙа аңлайышлы башҡалар араһында ныҡ айырылып тора, ул иҫбатлау талап иткән теоремаға оҡшаш. Евклид, күрәһең, быны тойомлағандыр, шунлыҡтан «Башланғыстар»ҙағы тәүге 28 һөйләм уның ярҙамынан тыш иҫбатлана.
«Евклидҡа параллель һыҙыҡтар тураһындағы постулаттың төрлө төрҙәре барлығы һис шикһеҙ билдәле булғандыр»[4]. Ни өсөн ул быныһын, ҡатмарлы һәм шөкәтһеҙен, һайлаған? Был һайлау сәбәптәренә ҡағылышлы тарихсылар төрлө фараздар ҡуҙғатты. Вольдемар Петрович Смилга фекеренсә, Евклид ошо бирелеш аша теорияның был өлөшө тамамланмағанлығын һыҙыҡ өҫтөнә алғандыр[10]. Морис Клайн иғтибарҙы шуға йүнәлтә: Евклидтың бишенсе постулаты локаль булып тора, йәғни яҫылыҡтың сикләнгән өлөшөндәге ваҡиғаға ғына ҡағыла, ә, мәҫәлән, Прокл аксиомаһы сикһеҙ тура һыҙыҡҡа ҡағылышлы параллеллек фактын раҫлай[11]. Шуныһын да оноторға ярамай: антик математиктар актуаль сикһеҙлекте ҡулланыуҙан ҡасҡан; мәҫәлән, Евклидтың икенсе постулаты тура һыҙыҡтың сикһеҙлеген раҫламай, ә бары тик «тура һыҙыҡты өҙлөкһөҙ дауам итеп булыуын ғына» күҙҙә тота. Антик математиктарға параллель һыҙыҡтар тураһында постулаттың үрҙә килтерелгән эквиваленттары яраҡһыҙ булып күренгән: улар йә актуаль сикһеҙлеккә йәки (әлегә индерелмәгән) үлсәм төшөнсәһенә һылтанған, йә уларҙы бик үк аңлайышлы түгел тип тапҡан. Тағы бер версияны тарихсы Имре Тот[12] тәҡдим итә: Евклидса бирелеш, моғайын, башта уның элгәрҙәренән берәйһенең (яңылыш иҫбат ителгән) теоремаһы булғандыр, һәм уны иҫбатлап булмаҫына инанғас, теорема статусын постулатҡа тиклем күтәргәндәрҙер, ә бирелеш тексын шул көйө ҡалдырғандарҙыр.
Абсолют геометрия[үҙгәртергә | сығанаҡты үҙгәртеү]
Аксиомалар исемлегенән V постулатты алып ташлағанда, килеп сыҡҡан аксиомалар системаһы абсолют геометрия тигән күренеште һүрәтләр. Атап әйткәндә, Евклид «Башланғыстар»ының тәүге 28 теоремаһы V постулатты файҙаланмайынса иҫбат ителә һәм шунлыҡтан абсолют геометрияға инә. Дауам итеү өсөн абсолют геометрияның ике теоремаһын билдәләйек:
- Параллель тура һыҙыҡтар бар; был Евклид «Башланғыстар»ының 27 һәм 28 теоремаларынан килеп сыға.
- Ике тура һыҙыҡты киҫешкән нөктәһенән ары дауам иткәндә, улар араһындағы арауыҡ сикһеҙ арта бара[13].
Иҫбатларға ынтылыштар[үҙгәртергә | сығанаҡты үҙгәртеү]
Математиктар борон замандарҙан уҡ «Евклидты яҡшыртырға» — йә бишенсе постулатты инеш раҫлауҙар араһынан алып ташларға, йәғни уны башҡа постулаттарға һәм аксиомаларға нигеҙләнеп иҫбатларға, йә уны башҡа постулаттар шикелле аңлайышлы башҡаға алмаштырырға тырышҡан. Евклидтың IV постулатының (бөтә тура мөйөштәр ҙә тигеҙ) ысынлап та артыҡ булып сығыуы — ул теорема кеүек итеп иҫбат ителгән дә аксиомалар исемлегенән һыҙып ташланған — уларҙың ыңғай һөҙөмтәгә өлгәшеренә өмөт өҫтәгән[5].
Ике мең йыл эсендә бишенсе постулатҡа бик күп иҫбатлау юлдары тәҡдим ителгән, ләкин иртәме-һуңмы уларҙың һәр береһендә етешһеҙлек түңәрәк табылған: шул бишенсе постулаттан башҡа иҫбатлап булмай торған әйберҙәр сыға ла тора икән.
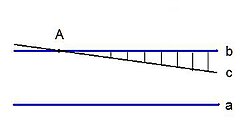
Прокл (б.э. V быуат) «Евклид Башланғыстарының I китабына комментарий»ында хәбәр итеүенсә, бындай иҫбатламаны Клавдий Птолемей индергән, ул был иҫбатламаны тәнҡитләй һәм үҙенекен тәҡдим итә[13]. Уны ябайлаштырып һүрәтләһәк, былай булыр: тура һыҙығы нөктәһе аша тура һыҙығына параллель үтә икән ти; иҫбат итәйек: теләһә ҡайһы башҡа бер тура һыҙыҡ , шул уҡ нөктә аша үткән осраҡта, тура һыҙығы менән киҫешә . Үрҙә телгә алынғанса, киҫешеү нөктәһенән ары киткәндә был тура һыҙыҡтарҙың араһы сикһеҙ ҙурая (тағы бер мәртәбә билдәләйек: был теореманы иҫбатлау V постулатҡа нигеҙләнмәй). Ләкин ул сағында менән араһындағы арауыҡ бер заман параллель тура һыҙыҡтар араһындағы арауыҡтан артып китә, йәғни менән тура һыҙыҡтары киҫешә.
Был иҫбатлама, ике параллель тура һыҙыҡ араһы даими (һәр хәлдә сикләнгән), тигән фаразға нигеҙләнә. Ләкин һуңынан асыҡланыуынса, был фараз V постулат менән тиң көскә эйә.
Б.э. тиклем I быуат ғалимы Посидоний параллель һыҙыҡтарҙы бөтә дауамында бер-береһенән тиң алыҫлыҡта тороусы тура һыҙыҡтар тип билдәләргә тәҡдим итә. Был билдәләмәнән бик еңел генә итеп бишенсе постулат сығарыла. Ләкин Посидонийҙың билдәләмәһе хаталы: бирелгән тура һыҙыҡтан тиң алыҫлыҡта булған һыҙыҡтың тура һыҙыҡ икәнлеге бер ерҙә лә күренмәй[14].
Антик мәҙәниәт юҡҡа сыҡҡандан һуң V постулат менән ислам илдәре математиктары шөғөлләнә башлай. Әл-Хәрәзми уҡыусыһы (IX быуат) әл-Жәүһәриҙең [15] иҫбатламаһы асыҡтан-асыҡ булмаһа ла шуны күҙҙә тота: ике тура һыҙыҡ өсөнсөһө тарафынан киҫелгәндә саттағы мөйөштәр тигеҙ булһа, шул уҡ ике тура һыҙыҡ теләһә ниндәй башҡа тура һыҙыҡ менән киҫелгәндә лә сат мөйөштәре тигеҙ була. Һәм был фараз V постулат көсөнә эйә.
Сабит ибн Курра (IX быуат) ике иҫбатлама бирә; беренсеһендә ул, ике тура һыҙыҡ бер-береһенән бер яҡлап алыҫлашһа, икенсе яҡлап улар бер-береһенә мотлаҡ яҡынлаша, тигән күҙаллауға таяна. Икенсеһендә ул, Посидоний кеүек үк, бер-береһенән тигеҙ алыҫлыҡта булған тура һыҙыҡтар барлығына нигеҙләнә, өҫтәүенә, ибн Курра был фактты «ябай хәрәкәт», йәғни тура һыҙыҡтан тигеҙ бер алыҫлыҡта барған хәрәкәт тураһындағы (уға был хәрәкәттең траекторияһы ла тура булып тойола) ҡараштан сығарырға тырыша[16]. Ибн Курраның был раҫламаларының икеһе лә V постулатҡа эквивалентлы.
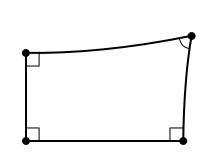
Ошондай уҡ хатаға ибн әл-Хайсам да юлыға, ләкин ул тәүләп һуңынан «Ламберт дүртмөйөшө» тигән исем аласаҡ фигураны ҡарай — был дүртмөйөштөң эске өс мөйөшө тура. Ул дүртенсе мөйөш өсөн ихтимал булған өс вариантты тәҡдим итә: ҡыҫынҡы, тура, йәйенке. Был өс гипотеза буйынса фекер алышыу һуңынан төрлө варианттарҙа ҡат-ҡат күтәрелә килә.
Шағир һәм математик Ғүмәр Хәйәм геометрияға механик хәрәкәтте индерергә тырышыуҙы тәнҡитләй. Ул V постулатты икенсе бер ябайыраҡҡа алмаштырырға тәҡдим итә: бер-береһенә яҡынайыусы тура һыҙыҡтар киҫешә, һәм бер-береһенә яҡынлашыусы ике тура һыҙыҡтың яҡынлашыу йүнәлешендә алыҫлашыуы мөмкин түгел. Был раҫламаның ике өлөшөнөң һәр береһе Евклид постулатына тиңдәш[17].
Әл-Әбхәри әл-Жәүһәри иҫбатламаһына оҡшаш иҫбатлама тәҡдим итә. Был иҫбатламаны үҙ китабында Шәмсуддин әс-Сәмәрҡәнди ҡуллана, шунлыҡтан тикшеренеүселәрҙең ҡайһы берҙәре уның авторы тип әс-Сәмәрҡәндиҙе һанай. Иҫбатлама абсолют геометрияла дөрөҫ булған раҫламанан сыға: бирелгән мөйөштөң яҡтарын киҫкән тура һыҙыҡ өсөн ошо уҡ мөйөштөң яҡтарын киҫеүсе һәм уның түбәһенән алыҫтараҡ ятыусы тағы бер тура һыҙыҡ үткәрергә мөмкин. Ләкин был раҫламанан автор логик яҡтан нигеҙләнмәгән һығымта яһай: бирелгән мөйөштөң эсендәге теләһә ҡайһы нөктә аша был мөйөштөң ике яғын да киҫә торған тура һыҙыҡ үткәреп була, ти һәм, V постулатҡа тиң һуңғы раҫламаһына нигеҙләнеп, артабанғы бөтә иҫбатлауын ҡора.
Насыр әд-Дин ат-Туси Ғүмәр Хәйәмдеке кеүек үк раҫлама тәҡдим итә[18]. Әйткәндәй, ат-Туси хеҙмәттәре Джон Валлисҡа билдәле була һәм шуның аша Европала Евклидтыҡы булмаған геометрия буйынса тикшеренеүҙәргә этәргес бирә.
Европала Евклидтың параллеллек аксиомаһын иҫбатларға беҙгә билдәле булған тәүге ынтылышты Прованста (Франция) йәшәгән Герсонид (Леви бен Гершом да ул, XIV быуат) яһай. Уның иҫбатламаһы тура дүртмөйөштөң барлығын раҫлауға таяна[19].
Иезуит ғалим Христофор Клавиус раҫламаһы XVI быуатҡа ҡарай. Уның иҫбатламаһы, ибн Курраныҡы кеүек үк, тура һыҙыҡтан тигеҙ алыҫлыҡтағы һыҙыҡтың да тура булыуына нигеҙләнә[20].
Джон Валлис 1693 йылда хеҙмәттәренең береһендә ат-Туси хеҙмәтенең тәржемәһен килтерә һәм эквивалентлы, ләкин ябайыраҡ бирелеш тәҡдим итә: оҡшаш, ләкин тигеҙ булмаған фигуралар бар[21].
Алекси Клод Клеро үҙенең «Геометрия башланғыстарында» (1741), Герсонид кеүек үк, V постулат урынына уның «тура дүртмөйөш бар» тигән эквивалентын ҡуллана.
Дөйөм алғанда был ынтылыштар тик файҙаға ғына була: V постулат менән башҡа раҫламалар араһында бәйләнеш асыҡлана, V постулатҡа ике альтернатива — ҡыҫынҡы һәм йәйенке мөйөш гипотезаһы — аныҡ итеп формалаштырыла.
Евклидтыҡы булмаған геометрияның тәүге һыҙмалары[үҙгәртергә | сығанаҡты үҙгәртеү]

V постулатты бөтөнләй өр-яңы күҙлектән тәрән итеп тикшереүҙе 1733 йылда итальян иезуит монахы математика уҡытыусыһы Джироламо Саккери атҡара. Ул «Бөтә таптарҙан таҙартылған Евклид, йәғни бөтә геометрияның иң тәүге башланғыстарын геометрик юл менән ҡорорға тырышыу» тигән исемдәге хеҙмәтен баҫтыра. Саккери идеяһы V постулатты ҡапма-ҡаршы менән алмаштырыуҙан, аксиомаларҙың яңы системаһынан мөмкин тиклем күберәк эҙемтәләр сығарыуҙан, шуның менән «ялған геометрия» төҙөп, был геометрияла ҡапма-ҡаршылыҡтар йәки ҡулланып булмаҫтай положениелар табыуҙан тора. Ул сағында V постулаттың дөрөҫлөгө ҡапма-ҡаршынан сығып иҫбатлана[22].
Саккери шул уҡ Ламберт дүртмөйөшөнөң 4-се мөйөшө тураһындағы өс гипотезаны ҡарай. Йәйенке мөйөш тураһындағы гипотезаны ул форма йәһәтенән шунда уҡ инҡар итә. Был осраҡта бөтә тура һыҙыҡтар ҙа киҫешкәнен күрһәтеү ауыр түгел, ә ул сағында Евклидтың V постулаты дөрөҫ тигән һығымта яһала — ул ҡайһы бер шарттарҙа тура һыҙыҡтар киҫешә тип раҫлай ҙа инде. Тимәк, «йәйенке мөйөш гипотезаһы тулыһынса һәм һәр ваҡыт ялған, сөнки ул үҙен-үҙе емерә» тигән һығымта килеп сыға[23].
Бынан һуң Саккери «ҡыҫынҡы мөйөш гипотезаһын» инҡар итергә тотона, бында инде уның тикшеренеүҙәре күпкә ҡыҙығыраҡ. Ул уны дөрөҫ тип таба һәм бер-бер артлы бер нисә эҙемтәне иҫбатлай. Үҙе лә һиҙмәҫтән, ул Лобачевский геометрияһын төҙөү яғына йүнәлеш ала. Саккери тарафынан иҫбат ителгән күп теоремалар интуиция кимәлендә ҡабул ителмәҫтәй тойолһа ла, ул теоремалар сылбырын дауам итә. Ниһайәт, Саккери «ялған геометрияла» теләһә ҡайһы ике тура һыҙыҡ йә киҫешә, йә уртаҡ перпендикулярға эйә була, улар йә был перпендикулярҙың ике яғында ла бер-береһенән алыҫлашалар, йә уның бер яғында бер-береһенән алыҫлашалар, ә икенсе яғында бер-береһенә сикһеҙ яҡынаялар, тип иҫбат итә. Ошо урында Саккери көтөлмәгән һығымта яһай: «ҡыҫынҡы мөйөш гипотезаһы тулыһынса ялған, сөнки тура һыҙыҡтың холҡона бөтөнләй тап килмәй»[24].
Күрәһең, Саккери был «иҫбатлауҙың» нигеҙһеҙлеген үҙе лә һиҙгәндер, сөнки тикшеренеүҙе дауам итә. Ул эквидистантаны — яҫылыҡта тура һыҙыҡтан бер иш алыҫлыҡта ятҡан нөктәләрҙең геометрик урынын — ҡарай; үҙ элгәрҙәренән айырмалы, Саккери был осраҡта бының тура һыҙыҡ түгеллеген аңлай. Ләкин, уның дуғаһының оҙонлоғон иҫәпләгәндә, Саккери хата ебәрә лә ҡаршылыҡҡа килеп төкәлә, артабан ул тикшеренеүҙе тамамлай һәм, еңел һулап, «был зарарлы гипотезаны тамырынан йолҡоп ташлауы» тураһында хәбәр итә. Ҡыҙғанысҡа ҡаршы, Саккери мәрхүм булғас баҫылып сыҡҡан был эш математиктарҙың тейешле иғтибарын тартмай һәм 150 йылдан ғына (1889) уның ватандашы Эудженио Бельтрами онотолған хеҙмәтте табып ала һәм уның тарихи әһәмиәтен баһалай.
XVIII быуаттың икенсе яртыһында парралель һыҙыҡтар теорияһы буйынса 50-ләгән хеҙмәт донъя күрә. Ул осорға яһалған күҙәтеүҙә (Георг Симон Клюгель) V постулатты иҫбат итергә ынтылыштарҙың 30-лаған осрағы ҡарала һәм уларҙың хаталы булыуы иҫбат ителә. Билдәле немец математигы һәм физигы Иоганн Генрих Ламберт та, Клюгель уның менән хатлашҡан, проблемаға ҡарата ҡыҙыҡһыныу күрһәтә; уның «Параллель һыҙыҡтар теорияһы» (Саккери хеҙмәте кеүек үк — мәрхүм булғас) 1786 йылда нәшер ителә.
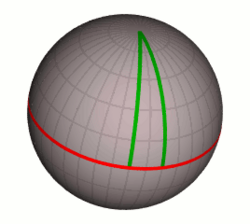
Ламберт «йәйенке мөйөш геометрияһының» сферала ҙур түңәрәктәрҙе тура һыҙыҡтар тип аңлаған осраҡта тормошҡа ашыуын беренсе булып аса. Ул, Саккери кеүек үк, «ҡыҫынҡы мөйөш гипотезаһынан» бик күп эҙемтәләр сығара, хатта Саккериҙы байтаҡҡа уҙып китә; атап әйткәндә, ул өсмөйөш мөйөштәре суммаһының өҫтәмәһе өсмөйөш майҙанына пропорциональ икәнен таба.
Үҙенең китабында Ламберт шулай тип билдәләй[25]:
|

Ламберт ҡыҫынҡы мөйөш гипотезаһында ҡапма-ҡаршылыҡ тапмай һәм, V постулатты иҫбат итеү мөмкин түгел, тигән һығымтаға килә. Ул «ҡыҫынҡы мөйөш геометрияһының» ялған булыуына бер шик тә белдермәй, ләкин, үткер иҫкәрмәһенә ҡарағанда, Ламберт Евклидтыҡы булмаған геометрияның ғәмәлләшеү ихтималлығы һәм бының фән өсөн ниндәй эҙемтәләре булыуы тураһында фекер йөрөткәндер[26]:
|
Ламберттың бик әһәмиәтле хеҙмәте, Саккери китабы кеүек үк, ваҡытынан күпкә алда хасил була һәм ул заман математиктарында бер ҡыҙыҡһыныу ҙа тыуҙырмай. Немец математиктары Фердинанд Карл Швейкарт (1817) менән Франц Адольф Тауринус (1826) «астраль геометрияһы» ла шул уҡ яҙмышҡа тарый, уларҙың идеяһы ла Ламберттыҡына яҡын була.
Шул уҡ ваҡытта Евклидтың «таптарын йыуырға» ынтылыштар дауам итә (Луи Бертран, Адриен Мари Лежандр, Семён Емельянович Гурьев һәм башҡалар). Лежандр V постулатҡа өс иҫбатлама бирә, ләкин уларҙың хаталы булыуын замандаштары бик тиҙ дәлилләй[27]. Һуңғы «иҫбатламаһын» ул 1823 йылда, Лобачевскийҙың яңы геометрия тураһындағы докладына тиклем өс йыл элек, нәшер итә.
Евклидтыҡы булмаған геометрияны асыу[үҙгәртергә | сығанаҡты үҙгәртеү]
XIX быуаттың беренсе яртыһында Саккери һалған һуҡмаҡтан Карл Фридрих Гаусс, Янош Бойяи, Н. И. Лобачевский һәм Фердинанд Карл Швейкарт юллана. Ләкин уларҙың маҡсаты башҡа — Евклидтыҡы булмаған геометрияны мөмкин булмаҫтай нәмә итеп фашлау түгел, ә, киреһенсә, альтернатив геометрия төҙөү һәм реаль донъяла уның ихтимал булған ролен асыҡлау. Заманы өсөн әҙәм ышанмаҫ идея була; быға тиклем бер ғалим да физик арауыҡтың Евклидтыҡы икәнлегендә шикләнмәй. Шуныһы ҡыҙыҡ: Гауссты ла, Лобачевскийҙы ла йәш саҡтарында бер үк уҡытыусы — Мартин Фёдорович Бартельс уҡыта, ләкин ул үҙе Евклидтыҡы булмаған геометрия менән шөғөлләнмәй.
Швайкарт беренсе була. 1818 йылда ул Гауссҡа, Евклидтыҡы булмаған геометрия нигеҙҙәрен етди анализлап, хат яҙып ебәрә, ләкин ҡарашын асыҡ фекер алышыуға сығарыуҙан тартына. Гаусс та был темаға яҙылған хеҙмәтте баҫтырырға баҙнат итмәй, ләкин уның ҡараламалағы яҙмалары һәм бер нисә хаты Евклидтыҡы булмаған геометрияны тәрән аңлауын раҫлай. Бына Гаусстың хаттарынан өҙөмтәләр, «Евклидтыҡы булмаған геометрия» тигән термин фәндә беренсе булып унда барлыҡҡа килә[28]:
|
1818 йылда Австрия астрономы Герлингҡа яҙған хатында Гаусс шөбһәләрен белдерә[30]:
|


Лобачевскийҙың «Параллель һыҙыҡтар теорияһы буйынса геометрик тикшеренеүҙәр» тигән хеҙмәте менән танышҡас, Гаусс бик әүҙем рәүештә урыҫ математигын Гёттинген король йәмғиәтенең сит ил мөхбир ағзаһы итеп һайлауҙы юллай башлай (1842 йылда был ғәмәлгә аша).
Лобачевский һәм Бойяи Гауссҡа ҡарағанда ҙурыраҡ ҡыйыулыҡ күрһәтә һәм икеһе бер юлы (Лобачевский — 1826 йылда докладында һәм 1829 йылда баҫма хеҙмәтендә; Бойяи — 1831 йылғы хатында һәм 1832 йылғы баҫма хеҙмәтендә), бер-береһенә бәйһеҙ рәүештә, хәҙерге ваҡытта Лобачевский геометрияһы тип аталған ғилемде һүрәтләй. Лобачевский яңы геометрияны эшләүҙә бөтәһенән дә алғараҡ китә, һәм ул хәҙер уның исемен йөрөтә. Ләкин уның төп ҡаҙанышы унда түгел, ә яңы геометрияға ышаныуында һәм ҡарашын ҡыйыу яҡлауында (ул хатта өсмөйөштөң мөйөштәрен үлсәү юлы менән V постулатты экспериментта тикшереп ҡарарға тәҡдим итә)[31].
«Геометрияның яңы башланғыстары» тигән китабының инешендә Лобачевский былай тип белдерә[32]:
|
Лобачевскийҙың фажиғәле яҙмышы, үтә ҡыйыу ҡараштары өсөн ғилми донъяла һәм эш урынында остракизмға дусар ителеүе Гаусстың хәүефләнеүҙәре нигеҙһеҙ түгеллеген раҫлай. Ләкин уның көрәше лә эҙһеҙ үтмәй. Яҙмыш шаяртыуы буйынса, ҡыйыу Лобачевский идеяларының тантанаһын үтә һаҡ Гаусс (үлгәндән һуң) тәьмин итә. 1860-сы йылдарҙа Гаусстың хаттары, шул иҫәптән Лобачевский геометрияһы тураһындағы һоҡланыулы фекерҙәре, донъя күрә, һәм был урыҫ математигының хеҙмәттәренә иғтибар йәлеп итә. 1868 йылда Эудженио Бельтрами мәҡәләһе баҫылып сыға, ул Лобачевский яҫылығының даими кире кәкрелеген раҫлай (Евклид яҫылығының кәкрелеге нуль, сфераныҡы — ыңғай); тиҙ арала Евклидтыҡы булмаған геометрия, әле һаман фекерҙә генә йәшәһә лә, легаль ғилми статус ала.
XIX быуат аҙағы — XX быуат башында тәүҙә математиктар (Бернхард Риман, Уильям Кингдон Клиффорд), шунан физиктар (Дөйөм сағыштырмалыҡ теорияһы, Эйнштейн), Евклидтың физик арауыҡ геометрияһы тураһындағы догматты юҡҡа сығара.
Бишенсе постулаттың бойондороҡһоҙлоғон иҫбатлау[үҙгәртергә | сығанаҡты үҙгәртеү]
Яңы геометрияның ҡапма-ҡаршылыҡһыҙ булыуын Лобачевский ҙа, Бойяи ҙа иҫбатлай алмай — ул саҡта математиканың ҡеүәтле саралары булмай. Тик 40 йылдан ғына Клейн моделе (1871) һәм Пуанкаре моделе (1882) барлыҡҡа килә, улар Лобачевский геометрияһының аксиоматикаһын Евклид геометрияһы нигеҙендә ғәмәлгә ашыра. Был моделдәр ышандырырлыҡ итеп шуны иҫбатлай: V постулатты инҡар итеү геометрияның башҡа аксиомаларына ҡаршы килмәй; тимәк, V постулат башҡа аксиомаларға бойондороҡло түгел һәм уны иҫбат итеү шулай уҡ мөмкин түгел.
Иҫкәрмәләр[үҙгәртергә | сығанаҡты үҙгәртеү]
- ↑ Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948. — Т. I. — С. 15.
- ↑ 2,0 2,1 Каган. Лобачевский, 1948, с. 164-165
- ↑ Смилга, 1988, с. 4
- ↑ 4,0 4,1 История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 110.
- ↑ 5,0 5,1 Мордухай-Болтовской Д. Д. Комментарии к «Началам» Евклида, книги I-VI. Указ. соч. — С. 241-244.
- ↑ Euclid’s Fifth Postulate
- ↑ Каган. Лобачевский, 1948, с. 167-175
- ↑ 8,0 8,1 8,2 Лелон-Ферран Ж., 1989, с. 255-256.
- ↑ Joel Castellanos. Non-Euclid. Axioms and Theorems (ингл.). Дата обращения: 11 февраля. Архивировано 19 август 2011 года.
- ↑ Смилга, 1988, с. 59-61
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 169.
- ↑ Tóth I. Das Parallelenproblem im Corpus Aristotelicum // Archive for history of exact sciences. — Berlin—Heidelberg—New York, 1967. — В. 4,5. — Т. 3. — С. 249-422.
- ↑ 13,0 13,1 Смилга, 1988, с. 72
- ↑ Лаптев Б. Л. Н. И. Лобачевский и его геометрия. — М.: Просвещение, 1976. — С. 71. — 112 с.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 231.
- ↑ Ибн Корра. Книга о том, что две линии, проведённые под углом, меньшим двух прямых, встречаются / Перевод и Иҫкәрмәләр Б. А. Розенфельда. — М.: ИМИ, 1963. — Т. XV. — С. 363—380.
- ↑ Хаййам. Трактаты / Перевод Б. А. Розенфельда. Редакция В. С. Сегаля и А. П. Юшкевича. Статья и комментарии Б. А. Розенфельда и А. П. Юшкевича. — М., 1962.
- ↑ Ат-Туси. Трактат, исцеляющий сомнение по поводу параллельных линий / Перевод Б. А. Розенфельда, Иҫкәрмәләр Б. А. Розенфельда и А. П. Юшкевича. — М.: ИМИ, 1960. — Т. XIII. — С. 483—532.
- ↑ Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
- ↑ Clavius C. Euclidis Elementorum, libri XV. — Romae, 1574.
- ↑ Wallis. Opera mathematica, v. II. — Oxoniae, 1693. — С. 665.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 215-217.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 100.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 105.
- ↑ Lambert J. H. Deutscher Gelehrter Briefwechsel. Bd. 1-5. Herausg. von J. Bernoulli. — Berlin, 1781—1784. — С. 202—203.
- ↑ Смилга, 1988, с. 121
- ↑ История математики, том III, стр. 218.
- ↑ Об основаниях геометрии, стр. 101-120.
- ↑ Икенсе хаттан билдәле булыуынса, үҙгәрмәүсән һан тигеҙ, бында кәкрелекте аңлата.
- ↑ Об основаниях геометрии, с. 119—120.
- ↑ Лобачевский Н. И. Сочинения по геометрии (Полн. собр. соч., тт. 1—3). — М. — Л.: ГИТТЛ, 1946—1949.
- ↑ Об основаниях геометрии, с. 61-62.
Әҙәбиәт[үҙгәртергә | сығанаҡты үҙгәртеү]
- Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948.
- Текст книг I—VI на www.math.ru или на mccme.ru 2011 йыл 11 август архивланған.
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — 468 с.
- Гильберт Д. Основания геометрии. — Л.: Сеятель, 1923. — 152 с.
- История математики с древнейших времён до начала XIX столетия. — М.: Наука, 1972.
- Каган В. Ф. Геометрия Лобачевского и её предыстория. — М.—Л., 1949.
- Каган В. Ф. Лобачевский. — Издание второе, дополненное. — М.-Л.: АН СССР, 1948. — 507 с.
- Лелон-Ферран Ж. Основания геометрии. — М.: Мир, 1989. — 312 с. — ISBN 5-03-001008-4.
- Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. — М., 1956.
- Розенфельд Б. А. История неевклидовой геометрии: Развитие понятия о геометрическом пространстве. — М.: Наука, 1976.
- Розенфельд Б. А., Юшкевич А. П. Теория параллельных линий на средневековом Востоке. — М.: Наука, 1983.
- Смилга В. П. В погоне за красотой. Занимательное введение в неевклидову геометрию. — 2-е изд. — М.: Молодая гвардия, 1988. — 288 с. — (Эврика).
- Успенский В. А. Апология математики. Глава 8. Параллельные прямые — в мифологии, реальности и математике. — М.: Амфора, 2009. — ISBN 978-5-367-00689-6.
Һылтанмалар[үҙгәртергә | сығанаҡты үҙгәртеү]
| Евклидтың параллеллек аксиомаһы Викимилектә |
- Александров А. Д. Тупость и гений. «Квант», №№ 11, 12 (1982). Дата обращения: 9 октября. Архивировано 19 август 2011 года.
- Возникновение неевклидовой геометрии. Дата обращения: 9 октября. Архивировано 19 август 2011 года.
- Пятый постулат Евклида. Дата обращения: 9 октября. Архивировано 21 август 2011 года. 2011 йыл 2 ноябрь архивланған.
Был мәҡәлә башҡорт Википедияһының һайланған мәҡәләләре исемлегенә керә. |






