Әйләнә

Әйләнә — яҫылыҡтың бирелгән нөктәнән бер тигеҙ алыҫлыҡта ятҡан бөтә нөктәләренән торған йомоҡ яҫы кәкре һыҙыҡ[1]. Был нөктә әйләнәнең үҙәге тип атала. Үҙәкте әйләнәнең ниндәй ҙә булһа нөктәһе менән тоташтырыусы киҫек радиус тип атала; радиус тип шулай уҡ был киҫектең оҙонлоғо атала. Әйләнә яҫылыҡты ике өлөшкә бүлә[2] — эске сикле һәм тышҡы сикһеҙ. Әйләнәнең эске өлөшө түңәрәк тип атала; ҡарашҡа бәйле рәүештә, түңәрәккә сикләүсе нөктәләр (йәғни әйләнә үҙе) инергә лә мөмкин йәки инмәҫкә лә мөмкин.

Практикала әйләнә циркуль ярҙамында төҙөлә. Нуль радиуслы әйләнә (әүерелгән әйләнә) нөктә була, әгәр иҫкәртеү булмаһа, артабан бындай осраҡ ҡаралмаясаҡ.
Әйләнә, әгәр уның радиусы бергә тигеҙ булһа, берәмек әйләнә тип атала. Берәмек әйләнә тригонометрияның төп объекттарының береһе булып тора.
Артабан бөтә урында ла хәрефе әйләнәнең радиусын аңлата.
Хордалар, дуғалар һәм тейеүселәр
[үҙгәртергә | сығанаҡты үҙгәртеү]-
Түңәрәктең секторҙары
Тура һыҙыҡтың әйләнә менән икенән артыҡ булмаған уртаҡ нөктәһе бар.
Әйләнәне төрлө ике нөктәлә киҫеүсе тура һыҙыҡ киҫеүсе тип атала. Киҫеүсенең әйләнә эсендә урынлашҡан киҫеге хорда тип атала. Әйләнәнең үҙәге аша үтеүсе хорда диаметр тип атала; шул уҡ термин уның оҙонлоғо өсөн дә ҡулланыла. Диаметр радиустан ике тапҡыр ҙур: ул әйләнәне ике тигеҙ өлөшкә бүлә һәм шуға күрә уның симметрия күсәре була. Диаметр башҡа теләһә ниндәй хорданан ҙурыраҡ[3].
Хорда түңәрәкте ике, түңәрәктең сегменты тип аталған өлөштәргә бүлә. Төрлө ике радиус шулай уҡ түңәрәкте ике, түңәрәктең секторҙары тип аталған өлөштәргә бүлә (см. рисунки)[3].
Әйләнәнең теләһә ниндәй ике тап килмәгән нөктәләре уны ике өлөшкә бүлә. Был өлөштәрҙең һәр береһе әйләнәнең дуғаһы тип атала. Әгәр дуғаның остарын тоташтырған киҫек диаметр булһа, дуға ярымәйләнә тип атала.
Бирелгән әйләнә өсөн түбәндәге үҙсәнлектәр хас[3].
- Үҙәктән бер тигеҙ алыҫлыҡта ятҡан хордалар тигеҙ. Киреһенсә, әгәр ике хорда оҙонлоғо буйынса тигеҙ булһа, ул саҡта улар үҙәктән бер тигеҙ алыҫлыҡта була.
- Тигеҙ хордаларға тигеҙ дуғалар ярашлы, һәм киреһенсә.

Әйләнә менән бер генә уртаҡ нөктәһе булған тура һыҙыҡ әйләнәгә тейеүсе тип атала, ә уларҙың уртаҡ нөктәһе тура һыҙыҡтың әйләнәгә тейеү нөктәһе тип атала. Әйләнәгә тейеүсе һәр саҡ уның тейеү нөктәһенә үткәрелгән радиусына (һәм диаметрына) перпендикуляр була. Йәғни радиус бер үк ваҡытта әйләнәгә нормаль була[4].
Әйләнәгә унан ситтә ятҡан нөктәнән үткәрелгән тейеүселәрҙең киҫектәре тигеҙ һәм был нөктә һәм әйләнәнең үҙәге аша үткән тура һыҙыҡ менән тигеҙ мөйөштәр яһайҙар.
Мөйөштәр
[үҙгәртергә | сығанаҡты үҙгәртеү]-
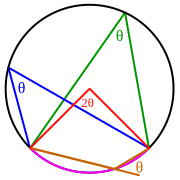
Ҡамалған мөйөш θ — шул уҡ дуғаға таянған 2θ үҙәк мөйөштөң яртыһына тигеҙ (алһыу төҫтә)
-
Дуғаның һәм хорданың оҙонлоғон иҫәпләүгә
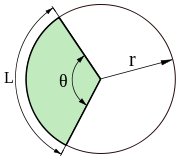
Үҙәк мөйөш — түбәһе әйләнәнең үҙәгендә булған мөйөш. Үҙәк мөйөш үҙе таянған дуғаның мөйөшсә үлсәме итеп ҡабул ителергә мөмкин. Оҙонлоғо буйынса радиусҡа тигеҙ булған әйләнәнең дуғаһы менән яһалған үҙәк мөйөш математикала мөйөштәрҙең үлсәү берәмеге итеп ҡабул ителә һәм радиан тип атала.
Радиандың билдәләмәһенән, әйләнәнең теләһә ниндәй дуғаһының оҙонлоғо , был дуғаға таянған үҙәк мөйөш менән ябай нисбәт менән бәйле булыуы килеп сыға[5]: (шуның менән бергә, шул уҡ дуғаны тартып торған хорда оҙонлоғо ) тигеҙ. Әйләнәнең оҙонлоғо тигеҙ булғанлыҡтан, мөйөш ҙурайыу менән уның радиандарҙа үлсәме 0-дән тиклем арта
Ҡамалған мөйөш — түбәһе әйләнәлә ятҡан, ә яҡтары был әйләнәне киҫкән мөйөш.
Ҡамалған мөйөш өсөн тышҡы мөйөш — ҡамалған мөйөштөң бер яғы һәм икенсе яғының дауамы менән яһалған мөйөш (һүрәттә θ мөйөшө көрән төҫтә). Ҡамалған мөйөш өсөн тышҡы мөйөш шул уҡ хордаға икенсе яҡтан таянған ҡамалған мөйөшкә тигеҙ. Әйләнә менән тура һыҙыҡ араһындағы мөйөш — киҫеүсе тура һыҙыҡ менән әйләнә һәм тура һыҙыҡ киҫешкән нөктәлә әйләнәгә үткәрелгән ике тейеүсенең береһе араһындағы мөйөш.
Ҡамалған мөйөштәрҙең үҙсәнлектәре:
- Ҡамалған мөйөш уның дуғаһына таянған үҙәк мөйөштөң яртыһына тигеҙ, йәки был мөйөштөң яртыһын 180°-ҡа тултыра. Ярымәйләнәгә таянған ҡамалған мөйөш һәр саҡ тура мөйөш була (90°-ҡа тигеҙ).
- Ҡамалған мөйөш уның түбәһен әйләнә буйлап күсергәндә дәүмәлен үҙгәртмәй.
- Бер үк дуғаға таянған ике ҡамалған мөйөш тигеҙ.
Башҡа үҙсәнлектәре:
- Әйләнәнән ситтә ятҡан нөктәнән үткәрелгән ике киҫеүсе араһындағы мөйөш был киҫеүселәр араһында ятҡан дуғаларҙың үлсәмдәренең ярымайырмаһына тигеҙ.
- Киҫешеүсе хордалар араһындағы мөйөш был мөйөштә ятҡан дуға менән уға ҡапма-ҡаршы ятҡан дуға үлсәмдәренең ярымсуммаһына тигеҙ.
- Уртаҡ нөктәләре булған тейеүсе менән хорда араһындағы мөйөш хорда тартып торған дуғаның мөйөшсә үлсәме яртыһына тигеҙ.
Үҙсәнлектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]- Изопериметрик тигеҙһеҙлек: Бирелгән оҙонлоҡтағы бөтә йомоҡ кәкре һыҙыҡтарҙан әйләнә иң ҙур майҙанлы өлкәне сикләй.
- Бер тура һыҙыҡта ятмаған өс нөктә аша әйләнә үткәрергә мөмкин һәм тик берҙе генә.
- Ике әйләнә, әгәр уларҙың берҙән бер уртаҡ нөктәһе булһа, тейешәләр тип әйтәләр. Ике әйләнәнең тейеү нөктәһе уларҙың үҙәктәре аша үткән тура һыҙыҡта ята.
- Киҫеүселәр тураһында теорема: Әгәр ирекле нөктә аша киҫеүсе үткәрелһә, ул саҡта был нөктәнән киҫеүсе менән әйләнә киҫешкән нөктәләргә тиклемге алыҫлыҡтар ҡабатландығы киҫеүсегә бәйле түгел (һәм нөктәнең әйләнәгә ҡарата дәрәжәһенең абсолют дәүмәленә тигеҙ). Әгәр нөктәһе әйләнәнән ситтә ятһа, ул саҡта был нөктәнән әйләнәгә тейеүсе үткәрергә мөмкин. Тейеүсенең тейеү нөктәһенә тиклемге киҫеге оҙонлоғоноң квадраты шул уҡ дәүмәлгә тигеҙ.
- Бынан алдағы үҙсәнлектең айырым осрағы булараҡ, ике хорда ирекле нөктәһендә киҫешкәндә, бер хорданың киҫектәре оҙонлоҡтарының ҡабатландығы икенсе хорданың киҫектәре оҙонлоҡтары ҡабатландығына тигеҙ була (һүрәтте ҡарағыҙ), йәғни .

Формулалар йыйылмаһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Әйләнәнең оҙонлоғо:
Әйләнәнең радиусы:
Әйләнәнең диаметры:
Радиусы R булған түңәрәктең майҙаны:
Радиусы R булған, градустарҙа үлсәнгән α үҙәк мөйөшө менән сикләнгән сектор майҙаны:
Хорда, үҙәк мөйөшө α булған әйләнә дуғаһы менән сикләнгән сегмент майҙаны:
Тарихы
[үҙгәртергә | сығанаҡты үҙгәртеү]Әйләнә, тура һыҙыҡ менән бер рәттән, кеше эшмәкәрлегенең төрлө өлкәләрендә иң киң таралған кәкре һыҙыҡ булып тора. Уны өйрәнеү һәм ҡулланыу тарихы бик борон замандарға барып тоташа; тәгәрмәс уйлап табыу был мәсьәләгә айырыуса мөһимлек бирә. Боронғо ғалимдар тура һыҙыҡ менән әйләнәне «камил» кәкре һыҙыҡтарҙың берҙән-бер миҫалы итеп ҡарайҙар, шуға күрә геометрияла тик циркуль һәм линейка ярҙамында төҙөүҙәр генә рөхсәт ителә тип һаналған, ә планеталар хәрәкәте әйләнәләр буйлап өйрөлөүҙәр һымаҡ моделләштерелә. Евклидтың «Башланғыстарының» III китабы әйләнәләр теорияһына арналған.
Әйләнә оҙонлоғоноң уның диаметрына сағыштырмаһы (π һаны) бөтә әйләнәләр өсөн дә бер үк икәнлеге шулай уҡ боронғо заманда асылған. Был сағыштырманы аныҡлау, шулай уҡ «түңәрәк квадратураһы» проблемаһын сисергә маташыу күп быуаттарға һуҙылған тарихи мөһим тема булып тора. Артабан әйләнәләр теорияһының үҫеше тригонометрияның, тирбәлеүҙәр теорияһының һәм фән һәм техниканың башҡа күп мөһим бүлектәренең барлыҡҡа килеүенә булышлыҡ итте.
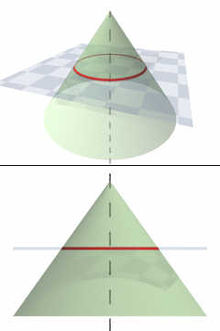
Әйләнәләрҙең аналитик геометрияһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Аналитик геометрия күҙлегенән ҡарағанда, әйләнә икенсе тәртиптәге ябай яҫы [[алгебраик кәкре һыҙыҡ|алгебраик] кәкре һыҙыҡ. Әйләнә является частным случаем эллипстың айырым осрағы булып тора, уның ярымкүсәрҙәре тигеҙ, һәм шуға күрә әйләнә конус киҫелештәренә инә.

Әйләнәнең дөйөм тигеҙләмәһе ошо күренештә яҙыла:
йәки
бында
нөктәһе — әйләнәнең үҙәге, — уның радиусы.
Радиусы үҙәге координаталар башы булған әйләнә тигеҙләмәһе:
Бер тура һыҙыҡта ятмаған нөктәләре аша үтеүсе әйләнә тигеҙләмәһе (Определитель ярҙамында):
Ул саҡта әйләнәнең үҙәге түбәндәге формулалар буйынса табыла:
Әйләнәне шулай уҡ параметрлы тигеҙләмә ярҙамында ла бирергә мөмкин:
Декарт координаталар системаһында әйләнә функцияның графигы булмай, ләкин ул түбәндәге ике функцияның графиктары берекмәһе итеп ҡаралырға мөмкин:
Әгәр әйләнәнең үҙәге координаталар башы менән тап килһә, функциялар түбәндәге күренеште ала:
Радиусы үҙәге нөктәһендә булған әйләнә:
Әгәр әйләнә үҙәгенең поляр координаталары булһа, ул саҡта координаталар башы аша үтеүсе әйләнә түбәндәге тигеҙләмә менән бирелә:
Әгәр әйләнәнең үҙәге координаталар башы булһа, тигеҙләмә түбәндәге күренештә була
Комплекслы яҫылыҡта әйләнә түбәндәге формула менән бирелә:
йәки параметрлы күренештә
Аралыҡта әйләнә
[үҙгәртергә | сығанаҡты үҙгәртеү]Аралыҡта радиусы үҙәге нөктәһендә булған әйләнәне
- сфераһының
- яҫылығы менән диаметраль киҫелеше контуры итеп ҡарарға мөмкин,
бында — бер үк ваҡытта нулгә тигеҙ булмаған параметрҙар; йәғни әйләнәлә ятҡан бөтә нөктәләр түбәндәге системаның сығарылышы
Мәҫәлән, булғанда был системаның сығарылыштарын параметр аша түбәндәгесә бирергә мөмкин:
Тейеүселәр һәм нормалдәр
[үҙгәртергә | сығанаҡты үҙгәртеү]Әйләнәгә нөктәһендә тейеүсенең тигеҙләмәһе түбәндәге тигеҙләмә менән бирелә
Шул уҡ нөктәлә нормалдең тигеҙләмәһе ошолай яҙыла
Концентрик һәм ортогональ әйләнәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]
Үҙәктәре уртаҡ, ләкин радиустары төрлө булған әйләнәләр концентрик әйләнәләр тип аталалар.
- тигеҙләмәләре менән бирелгән ике әйләнә
концентрик була шул саҡта һәм тик шул саҡта ғына, әгәр һәм булһа.
Ике әйләнә ортогональ була (йәғни тура мөйөш яһап киҫешәләр) шул саҡта һәм тик шул саҡта ғына, әгәр түбәндәге шарт үтәлһә
Өҫтәлмә мәғлүмәттәр
[үҙгәртергә | сығанаҡты үҙгәртеү]Бер әйләнә өсөн өсмөйөштәрҙе билдәләү
[үҙгәртергә | сығанаҡты үҙгәртеү]
- ABC өсмөйөшөнөң бөтә өс A, B һәм C түбәләре әйләнәлә ятһалар, ул (A,B,C) әйләнәһенә ҡамалған өсмөйөш тип атала. Был ваҡытта әйләнә ABC өсмөйөшөн ҡамаусы әйләнә тип атала (Ҡарағыҙ Ҡамаусы әйләнә).
- Әйләнәгә ҡамалған өсмөйөштөң теләһә ниндәй түбәһе аша үткәрелгән тейеүсе өсмөйөштөң был түбәгә ҡаршы ятҡан яғына антипараллель.
- ABC өсмөйөшөнөң бөтә өс AB, BC һәм CA яҡтары әйләнәгә ярашлы рәүештә ниндәйҙер C' , A' һәм B' нөктәләрендә тейһә, ул (A',B',C') әйләнәһен ҡамаусы өсмөйөш тип атала. Был осраҡта әйләнә ABC өсмөйөшөнә ҡамалған әйләнә тип атала (Ҡарағыҙ Ҡамалған әйләнә).
Әйләнә билдәләмәләренең төрлө варианттары
[үҙгәртергә | сығанаҡты үҙгәртеү]Был бүлектә мәғлүмәт сығанаҡтарына һылтанмалар етмәй. |
- Диаметры AB булған әйләнә — A, B нөктәләренән һәм яҫылыҡтың AB киҫеге тура мөйөш аҫтында күренгән бөтә нөктәләренән торған фигура (әйләнәнең диаметрына таяныусы мөйөш аша билдәләмә).
- Хордаһы AB булған әйләнә — яҫылыҡтың A, B нөктәләренән һәм AB киҫеге бер яҡтан AB дуғаһының ҡамалған мөйөшөнә тигеҙ булған даими мөйөш аҫтында күренгән һәм икенсе яҡтан, 180 градус минус юғарыла күрһәтелгән AB дуғаһының ҡамалған мөйөшөнә тигеҙ булған икенсе даими мөйөш аҫтында күренгән бөтә нөктәләренән торған фигура (ҡамалған мөйөш төшөнсәһе аша билдәләмә).
- AX һәм BX киҫектәре оҙонлоҡтарының сағыштырмаһы даими: булған нөктәләренән торған фигура әйләнә тип атала (Аполлоний әйләнәһе аша билдәләмә).
- Яҫылыҡтың, һәр береһенән бирелгән ике нөктәгә тиклемге алыҫлыҡтарының квадраттары суммаһы, был нөктәләр араһындағы алыҫлыҡ квадратының яртыһынан ҙурыраҡ булған бирелгән дәүмәлгә тигеҙ булған бөтә нөктәләренән торған фигура әйләнә тип атала (Гипотенузаһы әйләнәнең диаметры булған, әйләнәгә ҡамалған ирекле тура мөйөшлө өсмөйөш өсөн Пифагор теоремаһы аша билдәләмә).
- Әйләнә — йомоҡ, үҙ-үҙен киҫмәүсе, артабанғы үҙсәнлектәргә эйә булған фигура. Әгәр уның эсендә ятҡан ирекле E нөктәһе аша теләһә ниндәй AB, CD, GF һәм башҡа шулай хордалар үткәргәндә, тигеҙлеге дөрөҫ (һүрәтте ҡарағыҙ). Тигеҙлектәр E нөктәһен һәм уның аша үткәргән хордалар йүнәлешен һайлап алыуға бәйһеҙ рәүештә һәр ваҡыт үтәлә (Киҫешеүсе хордалар аша билдәләмә).

- Әйләнә — йомоҡ, үҙ-үҙен киҫмәүсе, артабанғы үҙсәнлектәргә эйә булған фигура. Әгәр унан ситтә ятҡан ирекле M нөктәһенән әйләнә менән тейеү нөктәләренә тиклем ике тейеүсе үткәрһәң, мәҫәлән, A һәм B, ул саҡта уларҙың оҙонлоҡтары һәр ваҡыт тигеҙ була: . Тигеҙлек M нөктәһен һайлап алыуға бәйһеҙ рәүештә һәр ваҡыт үтәлә (Тигеҙ тейеүселәр аша билдәләмә).
- Әйләнә — йомоҡ, үҙ-үҙен киҫмәүсе, артабанғы үҙсәнлектәргә эйә булған фигура. Уның теләһә ниндәй хордаһы оҙонлоғоноң был хордаға таянған теләһә ниндәй ҡамалған мөйөшө синусына сағыштырмаһы, был әйләнәнең диаметрына тигеҙ булған даими дәүмәл (синустар теоремаһы аша билдәләмә).
- Әйләнә — эллипстың айырым осрағы, уның фокустары араһындағы алыҫлыҡ нулгә тигеҙ (Үҙгәртелгән эллипс аша билдәләмә).
- Әйләнә булғандағы Синусоидаль спираль.
Ике әйләнәгә бәйле билдәләмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- Уртаҡ үҙәге булған ике әйләнә концентрик әйләнәләр тип аталалар.
- Бер генә уртаҡ нөктәһе булған ике әйләнә, әгәр уларҙың түңәрәктәренең башҡа уртаҡ нөктәһе булмаһа тыштан, ә әгәр уларҙың түңәрәктәре береһе икенсеһенең эсендә ятһа, эстән тейешеүсе әйләнәләр тип аталалар.
- Ике уртаҡ нөктәһе булған ике әйләнә киҫешеүсе әйләнәләр тип аталалар. Уларҙың түңәрәктәре (улар менән сикләнгән) икеләтә түңәрәк сегменты тип аталған өлкә буйынса киҫешәләр.
- Ике киҫешеүсе (йәки тейешеүсе) әйләнәләр араһындағы мөйөш тип әйләнәләргә уларҙың уртаҡ киҫешеү (йәки тейеү) нөктәһендә үткәрелгән тейеүселәр араһындағы мөйөш атала.
- Шулай уҡ ике киҫешеүсе (йәки тейешеүсе) әйләнәләр араһындағы мөйөш тип әйләнәләрҙең уларҙың уртаҡ киҫешеү (йәки тейеү) нөктәһендә үткәрелгән радиустары (диаметрҙары) араһындағы мөйөштө атарға мөмкин.
- Теләһә ниндәй әйләнә өсөн уның теләһә ниндәй нөктәһе аша үткәрелгән радиусы (йәки диаметры) һәм тейеүсе үҙ-ара перпендикуляр булғанлыҡтан, радиусты (йәки диаметрҙы) әйләнәгә был нөктәлә үткәрелгән нормаль тип иҫәпләргә мөмкин. Ошонан сығып, бынан алдағы ике пунктта билдәләнгән ике типтағы мөйөштәр, яҡтары үҙ-ара перпендикуяр булған мөйөштәр булараҡ, һәр ваҡыт бер-береһенә тигеҙ булалар.
- Тура мөйөш яһап киҫешкән ике әйләнә ортогональ әйләнәләр тип аталалар. Әйләнәләрҙе, әгәр улар бер-береһе менән тура мөйөш яһаһалар, ортогональ әйләнәләр тип иҫәпләргә була.
- Ике әйләнәнең радикаль күсәре — бирелгән ике әйләнәгә ҡарата дәрәжәләре тигеҙ булған нөктәләрҙең геометрик урыны. Икенсе һүҙ менән әйткәндә, был нөктәләрҙең геометрик урынындағы теләһә ниндәй M нөктәһенән бирелгән ике әйләнәгә үткәрелгән дүрт тейеүсенең оҙонлоҡтары тигеҙ.
Ике әйләнә өсөн мөйөштәр билдәләмәләре
[үҙгәртергә | сығанаҡты үҙгәртеү]- Ике киҫешеүсе әйләнә араһындағы мөйөш — әйләнәләргә уларҙың уртаҡ киҫешеү нөктәһендә үткәрелгән тейеүселәр араһындағы мөйөш. Ике киҫешеүсе әйләнә араһындағы ике мөйөш тә тигеҙ.
- Ике киҫешмәүсе әйләнә араһындағы мөйөш — ике әйләнәнең ике уртаҡ тейеүселәре киҫешеү нөктәһендә яһаған мөйөш. Был ике тейеүсенең киҫешеү нөктәһе ике әйләнә араһында ятырға тейеш, ә уларҙың береһе яғында түгел (был мөйөш ҡаралмай). Ике киҫешмәүсе әйләнә араһындағы ике вертикаль мөйөш тә тигеҙ.
Ортогоналлек
[үҙгәртергә | сығанаҡты үҙгәртеү]- Тура мөйөш яһап киҫешкән ике әйләнә ортогональ әйләнәләр тип аталалар. Әйләнәләрҙе, әгәр улар бер-береһе менән тура мөйөш яһаһалар, ортогональ әйләнәләр тип иҫәпләргә була.
- Үҙәктәре O һәм O' булған, A һәм B нөктәләрендә киҫешкән ике әйләнә, әгәр OAO' һәм OBO' мөйөштәре тура мөйөштәр булһалар, ортогональ тип атала. Тап ошо шарт ике әйләнә араһында тура мөйөштө гарантиялай. Был осраҡта ике әйләнәнең уларҙың киҫешеү нөктәһендә үткәрелгән радиустары (нормалдәре) перпендикуляр. Ошонан сығып, ике әйләнәнең уларҙың киҫешеү нөктәһендә үткәрелгән тейеүселәре лә перпендикуляр. Әйләнәнең тейеүсеһе тейеү нөктәһендә үткәрелгән радиусҡа (нормалгә) перпендикуляр. Ғәҙәттә кәкре һыҙыҡтар араһындағы мөйөш — уларҙың киҫешеү нөктәһендә үткәрелгән тейеүселәре араһындағы мөйөш.
- Икенсе өҫтәлмә шарт булырға мөмкин. A һәм B нөктәләрендә киҫешкән ике әйләнәгә C һәм D нөктәләрендә киҫешкән дуғаларҙың урталары инһен ти, йәғни AС дуғаһы СB дуғаһына тигеҙ, AD дуғаһы DB дуғаһына тигеҙ. Ул саҡта был ике әйләнә, әгәр СAD һәм СBD мөйөштәре тура мөйөштәр булһалар, ортогональ тип аталалар.
Өс әйләнәгә бәйле билдәләмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- Өс әйләнә, әгәр уларҙың теләһә ниндәй икәүһе бер-береһенә тейешһә (киҫешһә), үҙ-ара тейешеүсе (киҫешеүсе) тип аталалар.
- Геометрияла өс әйләнәнең радикаль үҙәге — әйләнәләрҙең өс радикаль күсәрҙәре парҙары киҫешкән нөктә. Әгәр радикаль үҙәк бөтә өс әйләнәнән ситтә ятһа, ул берҙән-бер әйләнәнең (радикаль әйләнәнең) үҙәге була, был әйләнә бирелгән өс әйләнәне ортогональ киҫә.
Архимед леммаһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Архимед леммаһы. Әгәр әйләнә хордаһы тартып торған әйләнә сегментына ҡамалһа һәм дуғаға нөктәһендә, ә хордаға — нөктәһендә тейһә, ул саҡта тура һыҙығы мөйөшөнөң биссектрисаһы була . Архимед леммаһы изоциркуляр үҙгәртеүҙәр төҙөгәндә мөһим роль уйнай.
Иҫбатлау
— бәләкәй әйләнәне ҙур әйләнәгә сағылдырыусы гомотетия булһын, ти. Ул саҡта был гомотетиның үҙәге булыуы аңлашылып тора. Ул саҡта тура һыҙығы ҙур әйләнәгә тейеүсе булған ниндәйҙер тура һыҙығына күсә, ә был тура һыҙыҡтағы һәм ҙур әйләнәгә ингән нөктәгә күсә. Гомотетия тура һыҙыҡтарҙы уларға параллель булған тура һыҙыҡтарға күсергәнлектән, . һәм — тура һыҙығындағы шундай нөктә булһын, бында — ҡыҫынҡы, ә — тура һыҙығындағы шундай нөктә, бында — ҡыҫынҡы. Ул саҡта, — ҙур әйләнәгә тейеүсе булғанлыҡтан . Ошонан сығып — тигеҙ эргәле, тимәк , йәғни — мөйөшөнөң биссектрисаһы.
Дүрт пар-пар тейешеүсе әйләнәләр радиустары өсөн Декарт теоремаһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Декарт теоремаһы, теләһә ниндәй дүрт үҙ-ара тейешеүсе әйләнәләрҙең радиустары ниндәйҙер квадрат тигеҙләмәне ҡәнәғәтләндерә тип раҫлай. Ҡайһы берҙә уларҙы Содди әйләнәләре тип атайҙар.
Күп үлсәмле дөйөмләштереү
[үҙгәртергә | сығанаҡты үҙгәртеү]Дөйөмләштерелгән әйләнәгә алыҫлыҡ төшөнсәһе бирелгән теләһә ниндәй математик структура өсөн билдәләмә бирергә мөмкин. Айырып әйткәндә, күп үлсәмле Евклид арауығы өсөн дөйөмләштерелгән әйләнә гиперсфера була; өс үлсәмле арауыҡта был ғәҙәттәге сфера. Сферик геометрияла сфералағы үҙәктәре сфераның үҙәге менән тап килгән әйләнәләр («ҙур түңәрәктәр») мөһим роль уйнайҙар.
Шулай уҡ ҡарағыҙ
[үҙгәртергә | сығанаҡты үҙгәртеү]- Глоссарий планиметрии на слово "Окружность"
- Вневписанная окружность
- Вписанная и вневписанные в треугольник окружности
- Вписанная окружность
- Категория:Әйләнәләр — әйләнәләр өсөн төп төшөнсәләр һәм теоремалар
- Ҡамаусы әйләнә
- Циклоида
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ Математическая энциклопедия, 1984, с. 15—16
- ↑ Элементарная математика, 1976, с. 408—409
- ↑ 3,0 3,1 3,2 Элементарная математика, 1976, с. 410—411
- ↑ Элементарная математика, 1976, с. 409—410
- ↑ Элементарная математика, 1976, с. 510
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]- Атанасян Л. С., Бутузов В. Ф.. и др. Дополнительные главы к учебнику 8 класса // Геометрия. — 3-е издание. — М.: Вита-Пресс, 2003.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70.
- Маркушевич А. И. Замечательные кривые, выпуск 4. — М.: Гостехиздат, 1952. — 32 с. Архивировано 14 сентябрь 2008 года.
- Окружность // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
Һылтанмалар
[үҙгәртергә | сығанаҡты үҙгәртеү]- Окружность на www.univer.omsk.su.
- Круг и окружность на сайте Метмат (методика преподавания математики).












































![{\displaystyle {\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c12fa86cb1797c21874c93d0344e32228f0acf62)






























