Мөйөш

	Мөйөш
	∠
Үлсәнеш	үлсәмһеҙ
Үлсәү берәмеге
СИ	радиан
Башҡа берәмектәр	градус, минут, секунд, град, меңенсе

Был терминдың башҡа мәғәнәләре лә бар, ҡарағыҙ: Мөйөш (мәғәнәләр).

Мөйөш — ул бер нөктәнән (мөйөштөң түбәһе) сыҡҡан ике нурҙан (мөйөштөң яҡтары) торған геометрик фигура^[1].

Дөйөм мәғлүмәттәр

Мөйөштөң ике яғы ятҡан яҫылыҡ мөйөш тарафынан ике өлкәгә бүленә. Был өлкәләрҙең һәр береһенең мөйөштөң яҡтары менән берекмәһе яҫы мөйөш (йәки мөйөш тип кенә) тип атала. Ҡайһы берҙә яҫы мөйөштәрҙең береһен (ғәҙәттә ике мөйөштөң бәләкәйерәген) шартлы рәүештә эске, ә икенсеһен — тышҡы мөйөш тип атайҙар. Яҫы мөйөштөң яҡтарында ятмаған нөктәләре яҫы мөйөштөң эске өлкәһен төҙөйҙәр.

Билдәләмәнең икенсе, эквивалентлы вариантында яҫы мөйөш тип яҫылыҡтың, бирелгән нөктәнән (мөйөштөң түбәһенән) сыҡҡан һәм был яҫылыҡта ятҡан ниндәйҙер һыҙыҡты (был яҫы мөйөштө тартып тороусы һыҙыҡ тип атала) киҫеп үткән бөтә нурҙарының берекмәһе булған өлөшө атала.

Йыш ҡына ҡыҫҡаса мөйөш тип шулай уҡ мөйөш үлсәмен, йәғни, мөйөштөң дәүмәлен билдәләүсе һанды атайҙар.

Төрлө үлсәнештәге метрик арауыҡтарҙа Евклид геометрияһында һәм шулай уҡ геометрияның башҡа төрҙәрендә, йыш осраған яҫы мөйөштәрҙән башҡа, мөйөш сифатында дөйөмөрәк объекттар — киҫешеүсе дуғалар, ярымяҫылыҡтар һәм башҡа фигуралар барлыҡҡа килтергән фигуралар ҡаралырға мөмкин.

Мөйөштәрҙең тамғаланышы

Мөйөштө тамғалау өсөн дөйөм ҡабул ителгән, 1634 йылда француз математигы Пьер Эригон тәҡдим иткән символ: $\angle ,$ ҡулланыла.

Математик аңлатмаларҙа мөйөштәрҙе йыш ҡына бәләкәй грек хәрефтәре менән тамғалайҙар: α, β, γ, θ, φ һәм башҡалар. Ҡағиҙә булараҡ, мөйөштөң эске өлкәһен һайлағанда билдәһеҙлекте булдырмаҫ өсөн, бирелгән тамғалауҙар һыҙмала күрһәтелә. пи һаны менән буталыш килеп сыҡмаһын өсөн, π символы был маҡсатта ҡулланылмай. Есемле мөйөштәрҙе тамғалау өсөн (аҫтараҡ ҡарағыҙ) йыш ҡына ω һәм Ω хәрефтәре ҡулланыла.

Мөйөштө шулай уҡ өс нөктә символы менән тамғалайҙар, мәҫәлән $\angle ABC.$ Был яҙылышта $B$ — түбәһе, ә $A$ һәм $C$ — мөйөштөң төрлө яҡтарында ятҡан нөктәләр. Математикала мөйөштәрҙе сәғәт уғына ҡаршы иҫәпләү йүнәлеше ҡабул ителгәнлектән, мөйөштөң тамғаланышында яҡтарында ятҡан нөктәләрҙе шулай уҡ сәғәт уғына ҡаршы һанап сығыу ҡабул ителгән. Был килешеү яҡтары уртаҡ, ләкин эске өлкәләре төрлө булған ике яҫы мөйөштө айыра белеүҙе тәьмин итә. Яҫы мөйөштөң эске өлкәһен һайлау контекстан билдәле булған, йәки икенсе ысул менән күрһәтелгән осраҡтарҙа, был килешеү үтәлмәҫкә мөмкин. Ҡарағыҙ. #Вариациялар һәм дөйөмләштереүҙәр.

Һирәгерәк мөйөштөң яҡтарын барлыҡҡа килтергән тура һыҙыҡтарҙың тамғалауҙары ҡулланыла. Мәҫәлән, $\angle (bc)$ — бында $\angle BAC$ өсмөйөшөнөң эске мөйөшө күҙ уңында тотола тип уйлана, α, уны $\angle (cb)$ тип тамғаларға кәрәк булған булыр ине.

Шулай, һүрәттә уңдан γ, $\angle ACB$ һәм $\angle (ba)$ яҙыуҙары бер үк мөйөштө аңлаталар.

Ҡайһы берҙә мөйөштәрҙе тамғалау өсөн бәләкәй латин хәрефтәре (a, b, c, …) һәм цифрҙар ҡулланыла.

Һүрәттәрҙә мөйөштәр, мөйөштөң эске өлкәһендә һыҙылған, үҙәге мөйөш түбәһендә булған ҙур булмаған бер, ике йәки өс дуға менән билдәләнәләр. Мөйөштәрҙең тигеҙлеге бер үк һандағы дуғалар йәки дуғала бер үк һандағы арҡыры штрихтар менән күрһәтелергә мөмкин. Әгәр мөйөштөң иҫәпләү йүнәлешен күрһәтергә кәрәк булһа, ул дуғала уҡ менән билдәләнә. Тура мөйөштәр дуға менән түгел, ә ике тоташҡан тигеҙ киҫектәр менән күрһәтелә, улар мөйөштөң яҡтары менән, бер түбәһе мөйөштөң түбәһе менән тап килгән бәләкәй квадрат барлыҡҡа килтерерлек итеп урынлаштырылалар.

Мөйөш үлсәме

Яҫы мөйөштәрҙе сағыштырырға мөмкинлек биреүсе мөйөш үлсәме ошолай индерелергә мөмкин. Ике яҫы мөйөш, әгәр уларҙы түбәләре һәм ике яғы тап килерлек итеп тура килтереп һалып булһа, тигеҙ (йәки конгруэнт) тип аталалар. Яҫылыҡта теләһә ниндәй нурҙан бирелгән яҡта бирелгән мөйөшкә тигеҙ булған берҙән бер мөйөш һалып була. Әгәр ике мөйөштөң түбәләре һәм бер яғы тап килерлек итеп, бер мөйөштө тулыһынса икенсе мөйөштөң эсендә урынлаштырып булһа, ул саҡта беренсе мөйөш икенсеһенән бәләкәй була. Ике мөйөш, бер мөйөштөң яғы икенсеһенең яғы менән тап килһә (тимәк, түбәләре лә тап килә), ләкин уларҙың эске өлкәләре киҫешмәһә, теркәлгән мөйөштәр тип аталалар. Ике теркәлгән мөйөштөң тап килмәүсе яҡтары төҙөгән мөйөштө был мөйөштәрҙең ҡушылдығы тип әйтәләр. Һәр мөйөшкә түбәндәгесә һанды (мөйөш үлсәмен) ярашлы итеп ҡуйып була:

тигеҙ мөйөштәргә тигеҙ мөйөш үлсәме ярашлы;
бәләкәйерәк мөйөшкә бәләкәйерәк мөйөш үлсәме ярашлы;
яҡтары тап килгән мөйөштөң (нуль мөйөштөң) мөйөш үлсәме нулгә тигеҙ (ошо уҡ параллель тура һыҙыҡтар араһындағы мөйөш өсөн дә дөрөҫ);
һәр нулдән айырмалы мөйөштөң нулдән ҙурыраҡ билдәле бер мөйөш үлсәме бар;
(аддитивлыҡ) мөйөштөң мөйөш үлсәме, уның яҡтары араһынан үтеүсе теләһә ниндәй нур тарафынан бүленгән мөйөштәрҙең мөйөш үлсәмдәре суммаһына тигеҙ.

Ҡайһы бер тамғалауҙар системаларында, әгәр мөйөш менән уның үлсәмен айырып ҡарарға кәрәк булһа, мөйөш (геометрик фигура) өсөн $\angle ABC,$ тамғалауы ҡулланыла, ә был мөйөштөң үлсәү берәмеге дәүмәле өсөн — ${\widehat {ABC}}$ тамғалауы ҡулланыла.

Мөйөштө үлсәйҙәр:

Иң таралған градус үлсәме — градус, минут, секунд, бында 1° итеп йәйелмә мөйөштөң 1/180 өлөшө ҡабул ителә (ҡарағыҙ. түбәндәрәк), бер минут $1'=1^{\circ }/60$ , һәм бер секунд $1''=1'/60$ . Градус үлсәме элементар геометрияла ҡулланыла (һыҙмаларҙа мөйөштәрҙе транспортир менән үлсәү), геодезияла карта буйынса һәм урында (мөйөштәрҙе урында үлсәү өсөн бик теүәл прибор — универсал/теодолит ҡулланыла).

Мөйөштөң радиан үлсәме — тартып тороусы дуға s оҙонлоғоноң уның r радиусына сағыштырмаһы (СИ системаһында). Радиан үлсәме математик анализда (мәҫәлән, тригонометрик функцияларҙың һанлы аргументы итеп, һәм һан ҡиммәттәрен (кире аркфункцияларҙың таблицалағы һәм графиктағы) ҡиммәттәрен тапҡанда), планиметрияла һәм механикала (нөктә йәки күсәр тирәһендә боролошто һәм тригонометрик функциялар ярҙамында тасуирланыусы башҡа процестарҙы — тирбәлеүҙәрҙе, тулҡынды ҡарағанда) ҡулланыла һәм башҡалар.

Мөйөштәрҙе шулай уҡ әйләнештәрҙә үлсәргә мөмкин. Бер әйләнеш — тулы мөйөш (йәғни 360 градуслы мөйөш). Ирекле мөйөш тураһында, әгәр x — мөйөштө тартып тороусы дуғаның оҙонлоғо s-тың был дуға ингән әйләнә оҙонлоғо L-ға сағыштырмаһы булһа, ул x әйләнеш тәшкил итә тип әйтәләр.

Мөйөштәрҙе үлсәүҙең градлы үлсәме ҡулланыуға тарихи тәҡдим ителгән була, хәҙерге ваҡытта ул бер ерҙә лә ҡулланылмай, сөнки киң таралған алтмышарлы градус үлсәмен ҡыҫырыҡлап сығара алмай.

Мөйөштәрҙе градус үлсәмендә үлсәү Боронғо Вавилонға барып тоташа, унда алтмышарлы иҫәпләү системаһы ҡулланылған була, уның эҙе ваҡыт һәм мөйөштәр бүлемдәрендә һаҡланған.

1 әйләнеш = 2π радиан = 360° = 400 град.

СИ системаһында мөйөштөң төп үлсәү берәмеге булып радиан тора.

Диңгеҙ терминологияһында мөйөштәр румбтарҙа үлсәнә. 1 румб компастың тулы әйләнәһенең (360 градус) ¹⁄₃₂ өлөшө, йәғни 11,25 градус, йәки 11°15′.

Астрономияла экваториаль координаталар системаһында тура күтәрелеү мөйөшө һәм бер сәғәтлек мөйөш сәғәттәрҙә, минуттарҙа һәм секундтарҙа (ярашлы рәүештә тулы әйләнәнең ¹⁄₂₄, ¹⁄₁₄₄₀ һәм ¹⁄_86 400 өлөшөн тәшкил итеүсе) үлсәнә; был Ерҙең күсәре тирәһендә әйләнеүенең мөйөшсә тиҙлеге менән бәйле, яҡынса 24 сәғәттә 1 әйләнеш тәшкил итә^[2]. Шулай итеп, бер сәғәттә (минутта, секундта) күк сфераһы мөйөшсә үлсәмдә яҡынса 1 сәғәткә (минутҡа, секундҡа) «борола». Ҡалған мөйөшсә дәүмәлдәр астрономияла ғәҙәттә дуға градустарында, минуттарында һәм секундтарында күрһәтеләләр. Буталыш булмаһын өсөн, тура күтәрелеүҙең бер секунды (минуты) дуғаның 15 секундына (минутына) тигеҙ булыуын билдәләп китергә кәрәк.

Артиллерияла шулай уҡ меңенсе һәм мөйөш үлсәгес бүлемдәре ҡулланыла.

Поляр координаталарҙа нөктәне тиңләштереү, йәки объекттың, уның база торошона ҡарата ике үлсәмдә торошон тасуирлау кеүек ҡайһы бер контекстарҙа, бөтөн һандағы тулы боролошҡа айырылып торған мөйөштәр ысынында эквивалентлы булалар. Мәҫәлән, бындай осраҡтарҙа 15° һәм 360015° мөйөштәрҙе эквивалентлы тип иҫәпләргә мөмкин (= 15° + 360°×1000). Ишелмә кәкреләрҙә нөктәне тиңләштереү йәки объекттың уның башланғыс торошона ҡарата ике үлсәмдә дөйөм әйләнешен тасуирлау кеүек икенсе контекстарҙа, нулдән айырмалы бөтөн һандағы тулы боролошҡа айырылып торған мөйөштәр эквивалентлы булмайҙар.

Ҡайһы бер яҫы мөйөштәрҙең махсус атамалары бар. Юғарыла һанап кителгән үлсәү берәмектәренән башҡа (радиан, румб, градус һәм башҡалар), уларға инәләр:

квадрант (тура мөйөш, әйләнәнең ¹⁄₄е);
секстант (әйләнәнең ¹⁄₆-е);
октант (әйләнәнең ¹⁄₈е; бынан тыш, стереометрияла октант тип өс үҙ-ара перпендикуляр яҫылыҡтар төҙөгән өс ҡырлы мөйөш атала),

Ҡайһы берҙә мөйөштәрҙе (мәҫәлән, йөҙҙөң ауышлыҡ мөйөшө) мөйөш үлсәменең үҙе менән үлсәмәйҙәр, ә уның тангенсы (йәки синусы менән), йәғни ауыш йөҙ буйынса үтелгән юлдың был юлдың горизонталь яҫылыҡҡа проекцияһы сағыштырмаһы менән (йәки был юлдың үҙенә) үлсәйҙәр. Ғәҙәттәге бәләкәй ауышлыҡ мөйөштәре булған осраҡтар өсөн был сағыштырма яҡынса радиандарҙа күрһәтелгән мөйөшкә тигеҙ (α < 0,1 булғанда tg α ≈ sin α ≈ α, был дәүмәлдәр араһында айырма 1%-тан кәм). Шуның менән бергә сағыштырма ғәҙәттә проценттарҙа йәки промиллеләрҙә күрһәтелә. Мәҫәлән, юлдың 10%-лы ауышлығы, юлдың һәр 100 метрына (горизонталгә проекцияһында) юл 10 м-ға күтәрелә тигәнде аңлата; горизонтҡа мөйөш arctg(10/100) ≈ 5,71° ≈ 0,1 радианға тигеҙ. Мөйөштәрҙе үлсәүҙең бындай ысулы, дөрөҫөн әйткәндә, мөйөш үлсәме түгел, сөнки аддитивлыҡ үҙсәнлегенә эйә түгел (ҡарағыҙ. юғарыла). Шулай уҡ ҡарағыҙ бәләкәй мөйөштәр өсөн яҡынлауҙар^[en].

Мөйөштәрҙе үлсәү йүнәлеше

Математикала һәм физикала, мөйөштәрҙе үлсәүҙең ыңғай йүнәлеше тип сәғәт уғына ҡаршы йүнәлеш ҡабул ителгән. Ғәҙәттә, мөйөштө башы координаталар системаһының (СК) үҙәге менән, ә йүнәлеше абсциссалар күсәренең ыңғай йүнәлеше менән тап килгән нурҙан башлап үлсәй башлайҙар (поляр КС, цилиндрик КС, сферик КС, тригонометрик әйләнәлә КС һәм башҡаларҙа).

Географияла һәм геодезияла азимут буйынса мөйөштәрҙең иҫәпләү башы итеп «төньяҡҡа» йүнәлеш ҡабул ителгән; мөйөш сәғәт уғы буйынса үлсәнә. Шулай итеп, «көнсығыш» йүнәлешкә 90° азимуталь мөйөш, «көньяҡҡа» — 180°, «көнбайышҡа» — 270° азимуталь мөйөш ярашлы. Артиллерияла поляр күсәрҙең «көньяҡҡа» йүнәлешенә өҫтөнлөк бирәләр һәм ярашлы поляр мөйөштө азимут тип атайҙар («көнбайышҡа» йүнәлеш 90°-лы азимуталь мөйөшкә ярашлы).

Шулай уҡ ҡарағыҙ: Тригонометрик әйләнә

Мөйөштәрҙең төрҙәре

Ҡыҫынҡы мөйөш
Йәйенке мөйөш
Ҡабарынҡы булмаған мөйөш
Тура мөйөш
Йәйелмә мөйөш
Тулы мөйөш

Мөйөштәр дәүмәленә бәйле рәүештә түбәндәгесә аталалар.

Нуль мөйөш (0°); нуль мөйөштөң яҡтары тап килә, уның эске өлкәһе — буш күмәклек.
Ҡыҫынҡы мөйөш (сик ҡиммәттәрен индермәйенсә, 0°-тан 90°-ҡа тиклем).
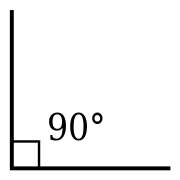
Тура мөйөш (90°); тура мөйөштөң яҡтары бер-береһенә перпендикуляр.
Йәйенке мөйөш (сик ҡиммәттәрен индермәйенсә, 90°-тан 180°-ҡа тиклем).
Ҡыя мөйөш (0°, 90°, 180° йәки 270°-ҡа тигеҙ булмаған теләһә ниндәй мөйөш).
Йәйелмә мөйөш (180°); йәйелмә мөйөштөң яҡтары булып бер тура һыҙыҡтың ике ярым тура һыҙығы, йәғни ҡапма-ҡаршы яҡҡа йүнәлгән ике нур тора.
Ҡабарынҡы мөйөш (0°-дән алып 180°-ты ла индереп, 180°-ҡа тиклем).
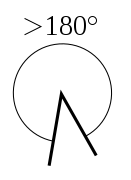
Ҡабарынҡы булмаған мөйөш (сик ҡиммәттәрен индермәйенсә, 180°-дән 360°-ҡа тиклем).
Тулы мөйөш (360°) — ҡарағыҙ. боролош (үлсәү берәмеге).

Шулай уҡ ҡарағыҙ: Үҙәк мөйөш

Биссектриса

Мөйөштөң биссектрисаһы (лат. bi- «икеләтә» һәм sectio «киҫеү» һүҙҙәренән) тип мөйөштөң түбәһенән сығып уның эске өлкәһе аша үткән һәм уның яҡтары менән ике тигеҙ мөйөш яһаған нур атала. Биссектрисаның теләһә ниндәй нөктәһенән уның яҡтарына тиклем алыҫлыҡ тигеҙ (һәм, киреһенсә, мөйөштөң эске өлкәһенең мөйөш яҡтарынан бер тигеҙ алыҫлыҡта ятҡан теләһә ниндәй нөктәһе уның биссектрисаһында ята).

Яҫы мөйөштәр

Яҫы мөйөш термины, мәҡәлә башында билдәләнгән мөйөш терминының синонимы һымаҡ, уны стереометрияла ҡулланылған есемле мөйөш төшөнсәһенән (шул иҫәптән ике ҡырлы, өс ҡырлы йәки күп ҡырлы мөйөштән) айырыу өсөн ҡулланыла.

Яҫы мөйөштәрҙең үҙсәнлектәре тип йыш ҡына мөйөштәрҙең (эргәләш, өҫтәлмә, теркәлгән, вертикаль — түбәндәрәк ҡарағыҙ), мөйөштәр бер яҫылыҡта ятҡан осрағында (планиметрия өсөн был үҙенән-үҙе аңлашылып тора, әммә стереометрия өсөн асыҡлау кәрәк, кире осраҡта түбәндә һанап кителгән нисбәттәр үтәлмәй, ә мөйөштәр үҙҙәре, әгәр бер яҫылыҡта ятмаһалар, эргәләш йәки теркәлгән тип аталмайҙар (вертикаль мөйөштәр автоматик рәүештә һәр саҡ бер яҫылыҡта яталар)) дәүмәлдәре нисбәтен аңлайҙар.

Вертикаль һәм теркәлгән мөйөштәр

Вертикаль мөйөштәр. Мөйөштәрҙең ике пары (A һәм B, C һәм D) пар-пар тигеҙ.
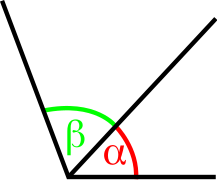
Теркәлгән мөйөштәр. Мөйөштәрҙең тышҡы (уртаҡ булмаған) яҡтары төҙөгән мөйөштөң дәүмәле теркәлгән мөйөштәрҙең үҙҙәренең дәүмәлдәренең суммаһына (α + β) тигеҙ
Өҫтәлмә мөйөштәр a һәм b (үҙ-ара бер береһен тура мөйөшкә тултыралар). Ике өҫтәлмә мөйөш тә ҡыҫынҡы мөйөш булалар
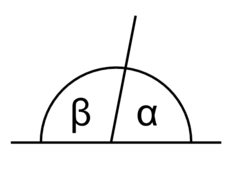
Эргәләш мөйөштәр — был һүрәттә ҡыҫынҡы (α) һәм йәйенке (β) — (α + β) йәйелмә мөйөшөн төҙөйҙәр
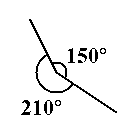
Эйәртеүле мөйөштәр — тулы мөйөш (360°) төҙөйҙәр; был һүрәттә айырым миҫал: 150° + 210° = 360°

Вертикаль мөйөштәр — ике тура һыҙыҡ киҫешкәндә барлыҡҡа килгән мөйөштәр, был мөйөштәрҙең уртаҡ яҡтары юҡ. Икенсе төрлө әйткәндә — ике мөйөш, әгәр бер мөйөштөң яҡтары икенсе мөйөштөң яҡтарының дауамы булып торһа, вертикаль мөйөштәр тип аталалар. Уларҙың төп үҙсәнлеге: вертикаль мөйөштәр тигеҙ.
Теркәлгән мөйөштәр — түбәһе һәм яҡтарының береһе уртаҡ, ләкин бер яҫылыҡта ятҡан эске өлкәләре киҫешмәгән ике мөйөш. Теркәлгән мөйөштәрҙең тышҡы (уртаҡ булмаған) яҡтары төҙөгән мөйөштөң дәүмәле теркәлгән мөйөштәрҙең үҙҙәренең дәүмәлдәренең суммаһына тигеҙ (һүрәттә α + β).

Теркәлгән мөйөштәрҙең айырым осраҡтары.

Әгәр теркәлгән мөйөштәр тигеҙ булһа, уларҙың уртаҡ яғы — биссектриса.

Өҫтәлмә мөйөштәр — түбәһе уртаҡ булған, яҡтарының береһе — уртаҡ, ә ҡалған яҡтары тура мөйөш төҙөгән ике мөйөш. Өҫтәлмә мөйөштәрҙең суммаһы 90°-ҡа тигеҙ. Мөйөштөң синусы, тангенсы һәм секансы ярашлы рәүештә өҫтәлмә мөйөштөң косинусына, котангенсына һәм косекансына тигеҙ.

Эргәләш мөйөштәр — түбәһе уртаҡ булған, яҡтарының береһе — уртаҡ, ә ҡалған яҡтары бер тура һыҙыҡта ятҡан (тап килмәйенсә) ике мөйөш. Эргәләш мөйөштәрҙең суммаһы 180°-ҡа тигеҙ.

Эйәртеүле мөйөштәр — түбәһе һәм ике яғы ла уртаҡ булған, ләкин эске өлкәләре төрлө булған ике мөйөш; бындай мөйөштәрҙең берекмәһе бөтә яҫылыҡты тәшкил итә, ә эйәртеүле мөйөштәр булараҡ улар икеһе бергә тулы мөйөш яһай; уларҙың дәүмәлдәренең суммаһы 360°.

Яҡтары (анти)параллель булған яҫы мөйөштәр

Яҡтары пар-пар параллель һәм бер йүнәлешле (йәки пар-пар параллель һәм ҡапма-ҡаршы йүнәлешле) мөйөштәр бер береһенә тигеҙ. Яҡтарының бер пары бер береһенә параллель һәм бер йүнәлешле, ә яҡтарының икенсе пары параллель һәм ҡапма-ҡаршы йүнәлешле булған мөйөштәр пары йәйелмә мөйөш төҙөйҙәр, йәғни суммаһы 180° (һүрәтте ҡарағыҙ) — сөнки уларҙы параллель күсереү ярҙамында эргәләш мөйөштәргә әйләндереп була (бер йүнәлешле яҡтарын «йәбештереп»).

Яҡтары үҙ-ара перпендикуляр булған мөйөштәр

Яҡтары үҙ-ара перпендикуляр булған ике мөйөш, әгәр улар икеһе лә ҡыҫынҡы йәки икеһе лә йәйенке булһа, тигеҙ булалар.

Өсмөйөштөң тышҡы мөйөшө

Төп мәҡәлә: Өсмөйөштөң тышҡы мөйөшө тураһында теорема

Өсмөйөштөң тышҡы мөйөшө тураһында теорема. Өсмөйөштөң тышҡы мөйөшө, уның тышҡы мөйөшө менән эргәләш булмаған, ҡалған ике мөйөшөнөң суммаһына тигеҙ.

Күпмөйөштөң мөйөштәре

Төп мәҡәлә: Күпмөйөштөң мөйөштәре суммаһы тураһында теорема

Яҡтары бер-береһе менән киҫешмәгән ирекле n-мөйөштөң эске мөйөштәренең суммаһы α_i $\sum _{i=1}^{n}\alpha _{i}=(n-2)\cdot 180^{\circ }$ тигеҙ.

Шулай,

өсмөйөштөң эске мөйөштәренең суммаһы 180°-ҡа тигеҙ,
дүртмөйөштөң — 360°,
бишмөйөштөң — 540° һәм шулай артабан.

Эҙемтә

Тышҡы мөйөш β_i тип (иғтибар, был тышҡы мөйөштөң ғәҙәттәге билдәләмәһе түгел) эске мөйөштө α_i тулы мөйөшкә тикдем тултырыусы мөйөштө атайыҡ: β_i = 360° − α_i.

Яҡтары бер-береһе менән киҫешмәгән ирекле n-мөйөштөң тышҡы мөйөштәренең суммаһы $\sum _{i=1}^{n}\beta _{i}=n\cdot 360^{\circ }-\sum _{i=1}^{n}\alpha _{i}=(n+2)\cdot 180^{\circ }$ тигеҙ

Үҙәк һәм ҡамалған мөйөш

Әйләнәнең теләһә ниндәй бирелгән дуғаһына берҙән-бер үҙәк һәм сикһеҙ күп ҡамалған мөйөштәрҙе ярашлы ҡуйып була.

Үҙәк мөйөш
Ҡамалған мөйөш

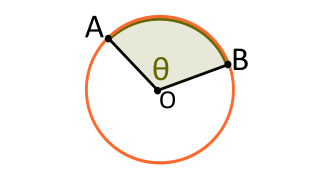
Үҙәк мөйөш — түбәһе әйләнәнең үҙәгендә булған мөйөш. Үҙәк мөйөштөң дәүмәле был мөйөштөң яҡтары араһындағы дуғаның градус үлсәменә тигеҙ.
Ҡамалған мөйөш — түбәһе әйләнәлә ятҡан, ә яҡтары был әйләнәне киҫеп үткән мөйөш. Ҡамалған мөйөштөң дәүмәле уның яҡтары менән сикләнгән дуғаның градус үлсәменең яртыһына тигеҙ. Бер үк дуғаға таянған бөтә ҡамалған мөйөштәр тигеҙ.

Ҡамалған мөйөштөң дәүмәле әйләнәлә шул уҡ дуғаға таянған үҙәк мөйөш дәүмәленең яртыһына тигеҙ (һүрәтте ҡарағыҙ.).

Вариациялар һәм дөйөмләштереүҙәр

$AB$ һәм $CD$ тура һыҙыҡтары араһындағы йүнәлешле мөйөштөң дәүмәле тип (тамғалау: $\angle (AB,CD)$ ), $AB$ тура һыҙығын, ул $CD$ тура һыҙығына параллель булһын өсөн сәғәт уғына ҡаршы йүнәлештә борорға кәрәк булған мөйөштөң дәүмәлен атайҙар. Шул уҡ ваҡытта n·180°-ҡа (n — бөтөн һан) айырылған мөйөштәрҙе тигеҙ тип һанайҙар. Әйтергә кәрәк, $CD$ һәм $AB$ тура һыҙыҡтары араһындағы йүнәлешле мөйөш $AB$ һәм $CD$ тура һыҙыҡтары араһындағы йүнәлешле мөйөшкә тигеҙ түгел (уларҙың суммаһы 180°, килешеү буйынса шул уҡ 0°). Йүнәлешле мөйөштәр ошондай үҙсәнлектәргә эйә: а) $\angle (AB,BC)=-\angle (BC,AB);$ б) $\angle (AB,CD)+\angle (CD,EF)=\angle (AB,EF);$ в) бер тура һыҙыҡта ятмаған $A,B,C,D,$ нөктәләре $\angle (AB,BC)=\angle (AD,DC)$ булғанда һәм бары тик шул саҡта ғына бер әйләнәлә яталар.

Күп кенә практик мәсьәләләр мөйөштө, беркетелгән нурҙы (нур сыҡҡан) О нөктәһе тирәләй бирелгән торошҡа тиклем борғанда барлыҡҡа килгән фигура итеп ҡарауҙың маҡсатҡа ярашлы булыуына килтерә.Был осраҡта мөйөш нурҙың боролоу үлсәме булып тора. Был билдәләмә, мөйөштөң билдәләнеү өлкәһен бөтә һанлы тура һыҙыҡҡа $(-\infty ;+\infty )$ киңәйтеп, мөйөш төшөнсәһен дөйөмләштерергә мөмкинлек бирә: 360°-тан ҙурыраҡ булған мөйөштәр индерелә, боролоу йүнәлешенә бәйле рәүештә ыңғай һәм тиҫкәре мөйөштәр айырыла. Ошолайтып ҡарау тригонометрияла тригонометрик функцияларҙы аргументтың теләһә ниндәй ҡиммәте өсөн өйрәнергә мөмкинлек бирә.

Мөйөш төшөнсәһе стереометрияла ҡаралған есемле мөйөшкә дөйөмләштерелә.

Есемле мөйөш

Төп мәҡәлә: Телесный угол

Есемле мөйөш яҫы мөйөштөң стереометрияға дөйөмләштерелеүе булып тора — ул арауыҡтың, бирелгән нөктәнән (мөйөштөң түбәһенән) сыҡҡан һәм ниндәйҙер (был есемле мөйөштө тарттырыусы йөҙ тип аталған) йөҙҙө киҫеп үтеүсе бөтә нурҙарҙың берекмәһе булып торған өлөшө.

Есемле мөйөштәр стерадиандарҙа үлсәнәләр (СИ системаһының төп берәмектәренең береһе), шулай уҡ системанан тыш берәмектәрҙә — тулы сфераның (йәғни 4π стерадиан тәшкил итеүсе тулы есемле мөйөштөң) өлөштәрендә, квадрат градустарҙа, квадрат минуттарҙа һәм квадрат секундтарҙа үлсәнәләр.

Есемле мөйөш булып, атап әйткәндә, түбәндәге геометрик есемдәр булалар:

ике ҡырлы мөйөш — арауыҡтың ике киҫешеүсе яҫылыҡ менән сикләнгән өлөшө;
өс ҡырлы мөйөш — арауыҡтың өс киҫешеүсе яҫылыҡ менән сикләнгән өлөшө;
күп ҡырлы мөйөш — арауыҡтың бер нөктәлә киҫешеүсе бер нисә яҫылыҡ менән сикләнгән өлөшө.

Ике ҡырлы мөйөш һыҙыҡлы мөйөш менән дә (уны төҙөүсе яҫылыҡтар араһындағы мөйөш), шулай уҡ есемле мөйөш менән дә (түбәһе сифатында уның ҡабырғаһындағы — ҡырҙары киҫешкән тура һыҙыҡтағы теләһә ниндәй нөктә һайлап алынырға мөмкин) характерланырға мөмкин. Әгәр ике ҡырлы мөйөштөң һыҙыҡлы мөйөшө (радиандарҙа) φ-гә тигеҙ булһа, уның есемле мөйөшө (стерадиандарҙа) 2φ-гә тигеҙ.

Кәкреләр араһында мөйөш

Планиметриялағы кеүек үк стереометрияла, шулай уҡ бер нисә башҡа геометрияларҙа киҫешеү нөктәләрендә шыма кәкреләр араһында мөйөштө ошолай билдәләргә мөмкин: билдәләмә буйынса уның дәүмәле кәкреләргә киҫешеү нөктәһендә үткәрелгән тейеүселәр араһындағы мөйөш дәүмәленә тигеҙ.

Мөйөш һәм скаляр ҡабатландыҡ

Мөйөш төшөнсәһен ирекле тәбиғәтле (һәм ирекле, шул иҫәптән сикһеҙ, үлсәмле), арауыҡтың ике $x$ һәм $y$ элементтары араһында аксиоматик рәүештә ыңғай билдәләнгән $(x,y)$ скаляр ҡабатландыҡ индерелгән һыҙыҡлы арауыҡ өсөн билдәләргә мөмкин. Скаляр ҡабатландыҡ шулай уҡ элементтың нормаһын (оҙонлоғон) элементтың үҙенә ҡабатландығының квадрат тамыры $||x||={\sqrt {(x,x)}}$ итеп билдәләргә мөмкинлек бирә. Скаляр ҡабатландыҡ аксиомаларынан скаляр ҡабатландыҡ өсөн Коши — Буняковский тигеҙһеҙлеге (Коши — Шварц) килеп сыға: $|(x,y)|\leqslant ||x||\cdot ||y||,$ бынан, ${\frac {(x,y)}{||x||\cdot ||y||}}$ дәүмәле −1-ҙән 1-гә тиклемге ҡиммәттәр ҡабул итеүе килеп сыға, шуның менән бергә ситтәге ҡиммәттәрен, элементтар бер-береһенә пропорциональ (коллинеар) булғанда һәм шул саҡта һәм бары шул саҡта ғына ҡабул итәләр (геометрик әйткәндә — уларҙың йүнәлештәре тап килгәндә йәки ҡапма-ҡаршы булғанда). Был ${\frac {(x,y)}{||x||\cdot ||y||}}$ сағыштырмаһын $x$ һәм $y$ элементтары араһындағы мөйөштөң косинусы итеп интерпретацияларға мөмкинлек бирә. Атап әйткәндә, әгәр элементтарҙың скаляр ҡабатландығы (йәки мөйөш косинусы) нулгә тигеҙ булһа, улар ортогональ тип аталалар.

Айырым алғанда, әгәр $(f,g)=\int _{a}^{b}f(x)g(x)dx$ стандарт скаляр ҡабатландыҡ индергәндә, ниндәйҙер $[a,b]$ интервалында өҙлөкһөҙ функциялар араһында мөйөш төшөнсәһе индерергә мөмкин, ул саҡта функцияларҙың нормалары $||f||^{2}=\int _{a}^{b}f^{2}(x)dx$ тип билдәләнә. Ул саҡта мөйөштөң косинусы стандарт рәүештә функцияларҙың скаляр ҡабатландығының уларҙың нормаларына сағыштырмаһы итеп билдәләнә. Функцияларҙы, әгәр уларҙың скаляр ҡабатландығы (уларҙың ҡабатландығының интегралы) нулгә тигеҙ булһа, шулай уҡ ортогональ тип атап була.

Риман геометрияһында оҡшаш рәүештә метрик тензор $g_{ij}$ ярҙамында тейеүсе векторҙар араһында мөйөшкә билдәләмә бирергә мөмкин. $u$ һәм $v$ тейеүсе векторҙарының скаляр ҡабатландығы тензорлы яҙыуҙа ошондай күренештә була: $(u,v)=g_{ij}u^{i}v^{j},$ ярашлы рәүештә векторҙарҙың нормалары — $||u||={\sqrt {|g_{ij}u^{i}u^{j}|}}$ һәм $||v||={\sqrt {|g_{ij}v^{i}v^{j}|}}.$ Шуға күрә мөйөштөң косинусы күрһәтелгән скаляр ҡабатландыҡтың векторҙарҙың нормаларына сағыштырмаһының стандарт формулаһы буйынса билдәләнергә мөмкин: $\cos \theta ={\frac {(u,v)}{||u||\cdot ||v||}}={\frac {g_{ij}u^{i}v^{j}}{\sqrt {|g_{ij}u^{i}u^{j}|\cdot |g_{ij}v^{i}v^{j}|}}}.$

Метрик арауыҡта мөйөш

Шулай уҡ метрик арауыҡтың элементтары араһында мөйөш төшөнсәһе индерелгән байтаҡ хеҙмәттәр бар.

$(X,\rho )$ — метрик арауыҡ булһын, ти. $x,y,z$ — был арауыҡтың элементтары икән ти.

К. Менгер түбәһе $x$ нөктәһендә булған $y$ һәм $z$ түбәләре араһында мөйөш төшөнсәһен тиҫкәре булмаған ${\widehat {yxz}}$ һаны булараҡ индерә, ул өс аксиоманы ҡәнәғәтләндерә:

${\widehat {yxz}}={\widehat {zxy}}$
${\widehat {yxz}}=0$ шул саҡта һәм шул саҡта ғына, әгәр $\rho (y,z)=|\rho (x,y)-\rho (x,z)|$ булһа
${\widehat {yxz}}=\pi$ шул саҡта һәм шул саҡта ғына, әгәр $\rho (y,z)=\rho (x,y)+\rho (x,z)$ булһа

1932 йылда Вильсон мөйөш сифатында түбәндәге аңлатманы ҡарай:

${\widehat {yxz}}_{w}=\arccos {\frac {\rho ^{2}(x,y)+\rho ^{2}(x,z)-\rho ^{2}(y,z)}{2\rho (x,y)\rho (x,z)}}$

Был аңлатманың һәр ваҡытта ла мәғәнәһе бар һәм Менгерҙың өс аксиомаһын ҡәнәғәтләндерә икәнен күреүе ҡыйын түгел.

Бынан тыш, Вильсондың мөйөшө ошондай үҙсәнлеккә эйә, ул Евклид арауығында Евклид арауығы мәғәнәһендә $y-x$ һәм $z-x$ элементтары араһындағы мөйөшкә эквивалентлы.

Мөйөштәрҙе үлсәү

Төп мәҡәлә: Средства для измерения углов

Мөйөштәрҙе төҙөү һәм үлсәү өсөн иң киң таралған инструменттарҙың береһе булып транспортир (шулай уҡ линейка — аҫтараҡ ҡарағыҙ) тора; ҡағиҙә булараҡ, ул билдәле бер дәүмәлдәге мөйөштө төҙөү өсөн ҡулланыла. Мөйөштәрҙе теүәлерәк үлсәү өсөн күп инструменттар эшләнгән:

мөйөш үлсәгес;
гониометр — мөйөштәрҙе лабораторияла үлсәү өсөн прибор;
кипрегель — геодезик мөйөш үлсәгес инструмент.

Күҙәтеүсе өсөн ике объект араһында мөйөш алыҫлығы (йәки мөйөш) тип, түбәһендә күҙәтеүсе торған, ә объекттар яҡтарында ятҡан мөйөш үлсәме атала. Ике алыҫтағы предметтар араһындағы мөйөштө яҡынса баһалау өсөн ҡул суғын файҙаланырға мөмкин. Һуҙылған ҡул алыҫлығында 1 градус (1°) мөйөш алыҫлығына сәтәкәй бармаҡ яҫылығы ярашлы (шулай уҡ аҫтараҡ ҡарағыҙ; урта бармаҡтың мөйөш киңлеге һуҙылған ҡул алыҫлығында яҡынса 2° тәшкил итә),10 градуслы мөйөшкә — горизонталь урынлашҡан төйөлгән йоҙроҡ киңлеге, (йәки ус арҡырыһы), 20 градуслы мөйөшкә (йәки яҡынса 15°÷17°÷20°) — айырылған ҙур һәм һуҡ бармаҡ остары араһындағы алыҫлыҡ (ҡарыш), ә сәтәкәй бармаҡ осонан баш бармаҡ осона тиклемге мөйөш алыҫлығы яҡынса тура мөйөштөң сирегенә тигеҙ. Былар яҡынса мәғлүмәт. Уларҙы үҙегеҙҙең ҡулығыҙ өсөн асыҡларға тәҡдим ителә.

Мөйөштәрҙе үлсәү өсөн төрлө ысулдар һәм ҡорамалдар мөйөш хәл ителеше, йәғни был ысул менән үлсәнергә мөмкин булған иң бәләкәй мөйөш менән характерлана. Дуғаның бер нисә микросекунды булған мөйөштәрҙе үлсәргә мөмкинлек биреүсе (~10⁻¹¹ радиан) интерферометрик ысулдар иң яҡшы мөйөш хәл ителешенә эйә.

Практик тригонометрик үлсәүҙәргә миҫалдар

Мәсьәләне ябай ысул менән сығарыу

Нисек өсмөйөштөң яҡтары ярҙамында һәм ҡул осондағы ҡорамалдар — миллиметрлы бүлемле линейка менән, (мәҫәлән, инженер/тригонометрик калькулятор (һәм таблицалар) һәм ПК (MS Office Excel) булмағанда cos иҫәпләү өсөн), мөйөштәрҙе (мәҫәлән, картала) үлсәргә?
Мөйөштөң яҡтарында 60 мм киҫек һалығыҙ һәм остарын киҫек менән тоташтырығыҙ. Был киҫектең миллиметрҙарҙа оҙонлоғо мөйөштөң градустарҙа яҡынса ҡиммәтен күрһәтә. Ошо ысул менән етерлек (ҡабул итерлек) теүәллек менән 60°-ҡа тиклемге ҡыҫынҡы мөйөштәрҙе үлсәргә мөмкин. Әгәр мөйөш 60°-тан ҙур булһа, уның 90°, 180, 270° йәки 360°-ҡа тиклем өҫтәмәһен үлсәйҙәр. 90° йәки 270°-ҡа тиклем өҫтәмәһен үлсәү өсөн мөйөш түбәһенән өсмөйөш ярҙамында яҡтарҙың береһенә перпендикуляр үткәрелә (тигеҙ эргәле өсмөйөштә — медиана-биссектриса, шул уҡ бейеклек була).

Һуҙылған ҡулдың тура мөйөшкә айырылған ҙур һәм һуҡ бармаҡтарына тоҫҡау мөйөшө яҡынса 15° тәшкил итә. Быны нисек тикшерергә һәм асыҡларға?
Иң беренсе урында ориентир билдәләгеҙ һәм унан 90° мөйөш һалығыҙ. Быны алдағы мәсьәләлә тасуирланған ысул менән эшләргә була. Артабан ориентирҙан тура мөйөшкә айырылған ҙур һәм һуҡ бармаҡтарға тоҫҡап 15° алты мөйөш һалығыҙ. Һуңғы мөйөштө һалыу урында тура мөйөш яһарға тейеш. Әгәр был теүәл килеп сыҡмаһа, һуҙылған ҡулда күҙҙән бер аҙ яҡыныраҡ йәки алыҫыраҡ (60 см тирәһе) тотоп, мөйөштәрҙе һалыуҙы ҡабатларға кәрәк. Ошоноң менән һеҙ 15° мөйөш һалыу өсөн ҡулды һуҙырға кәрәк булған алыҫлыҡты белерһегеҙ^[3].

Мөйөштәрҙе шулай уҡ төрлө үлсәү приборҙары һәм ҡулайламалар ярҙамында иҫәпләргә мөмкин — иҫәпләү линейкаһында тригонометрия ярҙамында, инженер калькуляторында (шул иҫәптән калькулятор (Windows)), MS Office Excel таблицаһы функциялары ярҙамында: (1) cos, (2) аҙаҡ arccos, һәм (3) шулай уҡ функциялар ярҙамында, радиандарҙың ҡиммәтен градустарға (°) күсерергә (ПК булғанда; бирелгән яҡтары буйынса өсмөйөштөң мөйөштәрен on-line-иҫәпләү бар); Шулай уҡ махсус тригонометрик таблицалар: sin, cos, шулай уҡ arccos, arcsin бар, һуңғылары, әйткәндәй, градустарға ҡайтарып иҫәпләү менән.

Аналитическая геометрияла координаталар яҫылығында тура һыҙыҡтар араһында мөйөш, мәҫәлән, түбәндәге тигеҙләмә менән бирелә:

\alpha =\mathrm {arctg} \,\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|

(ҡарағыҙ. Һыҙыҡлы функция; шулай уҡ ҡарағыҙ #Мөйөш һәм скаляр ҡабатландыҡ)

Иҫкәрмәләр

↑ Угол // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5.
↑ В действительности истинный период обращения Земли относительно неподвижных звёзд примерно на 4 минуты короче, чем 24 часа, см. звёздное время.
↑ Куприн А. М. На местности и по карте. — М. Недра, 1982. — 112 с.

Шулай уҡ ҡарағыҙ

Әҙәбиәт

Барабанов О. О. Начала истории прямого угла // История науки и техники, 2015. № 1. С. 16-27.* Погорелов А. В. Геометрия: учебник для 7—11 классов средней школы. — М.: Просвещение, 1992. — 383 с. — ISBN 9785090038546.
Сидоров Л. А. Угол // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1985. — Т. 5. — С. 459‒460. — 623 с. — 150 000 экз.
Двугранный угол // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1979. — Т. 2. — С. 50. — 552 с. — 150 000 экз.
Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30‒31. — ISBN 5-94057-170-0.
Угломерные приборы/Угол (плоский) // Большая Советская энциклопедия (в 30 т.) / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: «Советская Энциклопедия», 1977. — Т. XXVI. — С. 459‒460. — 624 с.
Weisstein, Eric W. Line Bisector (инг.) на сайте Wolfram MathWorld.
Weisstein, Eric W. Angle (инг.) на сайте Wolfram MathWorld.
Weisstein, Eric W. Polygon (инг.) на сайте Wolfram MathWorld.
K. Menger New Fondations of Euclidean Geometry (инг.) // THE AMERICAN JOURNAL OF MATHEMATICS 53 : журнал. — 1931. — С. 721‒745.
W. A. Wilson On angles in certain metric spaces (инг.) // Bulletin of American Mathematical Society 39. — 1932. — С. 580‒588.

[1] Угол // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5.

[2] В действительности истинный период обращения Земли относительно неподвижных звёзд примерно на 4 минуты короче, чем 24 часа, см. звёздное время.

[3] Куприн А. М. На местности и по карте. — М. Недра, 1982. — 112 с.

[1]

[2]

[3]

	угол Викиһүҙлектә
	Мөйөш Викимилектә