Алтымөйөш

Алтымөйөш
Алдағы	бишмөйөш
Тәртип буйынса һуңыраҡ килеүсе	Етемөйөш
Имеет вершинную фигуру	киҫек[d]
Грань политопа	ҡабырға
Вики-проект	Проект:Математика[d]
Алтымөйөш Викимилектә

Алтымөйөш — алты мөйөшө булған күпмөйөш. Шулай уҡ шундай формалағы теләһә ниндәй нәмә алтымөйөш тип атала.

Үҙе менән киҫешмәүсе алтымөйөш майҙаны

Түбәләренең координаталары менән бирелгән эргәләш булмаған яҡтары киҫешмәгән алтымөйөштөң майҙаны күпмөйөштәр өсөн дөйөм булған формула буйынса иҫәпләнә.

Ҡабарынҡы алтымөйөш

Ҡабарынҡы алтымөйөш тип, бөтә нөктәләре лә уның ике күрше түбәһе аша үтеүсе теләһә ниндәй тура һыҙыҡтан бер яҡта ятҡан алтымөйөш атала.

Ҡабарынҡы алтымөйөштөң эске мөйөштәренең суммаһы 720°-ҡа тигеҙ.

$\sum _{i=1}^{6}\alpha _{i}=(6-2)\cdot 180^{\circ }=4\cdot 180^{\circ }=720^{\circ }$

Төҙөк алтымөйөш

Төҙөк алтымөйөш

Бөтә яҡтары ла тигеҙ, ә бөтә эске мөйөштәре лә 120°-ҡа тигеҙ булған алтымөйөш төҙөк алтымөйөш тип атала.

Гексаграмма

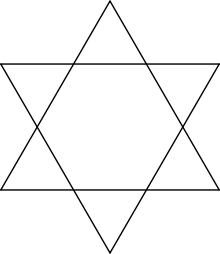
Йондоҙ һымаҡ алтымөйөштәр

Бөтә яҡтары һәм бөтә мөйөштәре тигеҙ булған, ә түбәләре төҙөк күпмөйөштөң түбәләре менән тап килгән күпмөйөш йондоҙ һымаҡ күпмөйөш тип атала. Төҙөк алтымөйөштән башҡа тағы ла бер йондоҙ һымаҡ алтымөйөш бар, ул ике төҙөк өсмөйөштән тора — гексаграмма йәки Давид йондоҙо.

Шулай уҡ ҡарағыҙ

• Бал ҡорттары кәрәҙе
• Паскаль теоремаһы һәм Брианшон теоремаһы
• Птолемей тигеҙһеҙлеге
• Гексагональ шахмат
• Гигант гексагон
• Задача со счастливым концом

Иҫкәрмәләр

<onlyinclude>

<onlyinclude>