Гамма-функция
| Гамма-функция | |
 | |
 | |
| Асыусы йәки уйлап табыусы | Леонард Эйлер[1] |
|---|---|
| Закон йәки теорема формулаһы | [2][3] |
| Обозначение в формуле | , һәм |
| Вики-проект | Проект:Математика[d] |
| Влечёт за собой | факториал |
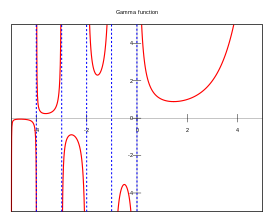
Гамма-функция — математик функция, ғәҙәттә тип тамғалана. Леонард Эйлер тарафынан индерелгән, ә үҙенең тамғаланышы менән гамма-функция Адриен Мари Лежандрға бурыслы.
Гамма-функция фәндә бик киң ҡулланыла. Уның киң ҡулланылған өлкәләре — математик анализ, ихтималлыҡ теорияһы, комбинаторика, статистика, атом физикаһы, астрофизика, гидродинамика, сейсмология. Айырым осраҡта, гамма-функция факториал төшөнсәһен аргументтың ысын һәм комплекслы ҡиммәттәре күмәклегенә дөйөмләштереү өсөн ҡулланыла.
Билдәләмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]
Интеграль билдәләмә
[үҙгәртергә | сығанаҡты үҙгәртеү]Әгәр комплекслы һанының ысын өлөшө ыңғай булһа, гамма-функция абсолют йыйылыусан интеграл аша билдәләнә: Был билдәләмә Лежандр тарафынан Эйлерҙың үҙенсәлекле билдәләмәһенән, үҙгәреүсәнде алмаштырып ҡуйыу юлы менән сығарылған (1730 й.)
Бөгөнгө көндә тап Лежандр билдәләмәһе гамма-функцияның классик билдәләмәһе булараҡ билдәле. Классик билдәләмәне өлөшләп интеграллап, булыуын күрергә мөмкин.
Гамма-функцияның ҡиммәтен яҡынса иҫәпләү өсөн, шулай уҡ Эйлер билдәләмәһенән тигеҙлеген ҡулланыу һәм үҙгәреүсәнде алмаштырып ҡуйыу юлы менән табылған өсөнсө формула уңайлы:
- .
Был формулала интеграл булғанда йыйылыусан, әммә ул ғәҙәттә үҙгәреүсәндең ыңғай ысын ҡиммәттәрендә (башлыса — 1-гә яҡын) ҡулланыла. Ысын аргументтың булған осрағында интеграл аҫты функцияһының берҙән-бер үҙенә бер төрлө нөктәһе бар — булғанда өҙөклөк бөтөрөлә, һәм әгәр уға нөктәһендә өҫтәп билдәләмә биргәндә, ул бөтә киҫегендә өҙлөкһөҙ буласаҡ. Шулай итеп, интеграл үҙинтеграл була, был һанлы интеграллауҙы ябайлаштыра.
Баштағы формуланың, Риман-Ханкель интегралы тип аталған бөтә комплекслы яҫылыҡҡа туранан-тура дауамы бар
бында контуры — комплекслы яҫылыҡтағы, нөктәһен сәғәт уғы йүнәлешенә ҡаршы урап сығыусы, остары ыңғай ысын күсәр буйлап сикһеҙлеккә киткән теләһә ниндәй контур.
Артабанғы аңлатмалар гамма-функцияның альтернатив билдәләмәләре булып торалар.
Гаусс билдәләмәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Ул 0 һәм тиҫкәре һандарҙан башҡа, бөтә комплекслы һандары өсөн дөрөҫ
Эйлер билдәләмәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Вейерштрасс билдәләмәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]бында — Эйлер — Маскерони даимиһы.
Иҫкәрмә: ҡайһы берҙә альтернатив, пи-функция ҡулланла, ул факториалдың һөҙөмтәһе булып тора һәм гамма-функция менән нисбәте менән бәйләнгән. Гаусс, Риман, һәм XIX быуаттың башҡа күп немец математиктары тап ошо функция (ә Г-функция түгел) менән ҡулланғандар.
Үҙсәнлектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]
Әгәр — бөтөн тиҫкәре булмаған һан булһа,
- .
Гамма-функцияның төп үҙсәнлеге — уның рекуррент тигеҙләмәһе
ул билдәләнгән башланғыс шарттарҙа берҙән-бер логарифмик асыҡ сағылышлы сығарылышын, йәғни гамма-функцияның үҙен билдәләй (берҙән-берлеге тураһында теорема).
Г-функция өсөн Эйлер өҫтәмәһе формулаһы дөрөҫ:
- .
Шулай уҡ Гаусстың ҡабатлау формулаһы ла дөрөҫ:
Был формуланың n=2 булғандағы Лежандр сығарған айырым осрағы:
Гамма-функцияның бөтә комплекслы яҫылыҡта нулдәре юҡ. комплекслы яҫылыҡта мероморфлы булып тора һәм нөктәләрендә ябай полюстары бар.
Гамма-функцияның теләһә ниндәй натураль һәм нуль өсөн нөктәһендә беренсе тәртиптәге полюсы бар; был нөктәлә ҡалдыҡ шулай билдәләнә:
- .
Файҙалы үҙсәнлек, уны сикләмәле билдәләмәнән килтереп сығарырға мөмкин:
- .
Гамма-функция сикһеҙ күп тапҡыр дифференциалланыусы функция, һәм , бында , йыш ҡына «пси-функция» тип йәки дигамма-функция тип атайҙар. Гамма-функция һәм бета-функция түбәндәге нисбәт менән бәйләнгәндәр:
- .
Гамма-функция логарифмы
[үҙгәртергә | сығанаҡты үҙгәртеү]Бик күп сәбәптәр буйынса гамма-функция менән бер рәттән йыш ҡына гамма-функцияның логарифммын — дигамма-функцияның сығарылмаһын ҡарайҙар. Уның өсөн түбәндәге интеграль күренештәр хас:
һәм
Был формулалар Жак Бине тарафынан 1839 йылда сығарылған (был формулаларҙы ярашлы рәүештә гамма-функцияның логарифмы өсөн Биненың беренсе һәм икенсе формулалары тип тә атайҙар)[4]. Гамма-функцияның логарифмы өсөн бер аҙ икенсерәк интеграль формулалар Карл Йохан Мальмстендың, Матиаш Лерхтың һәм бер нисә башҡа математиктарҙың хеҙмәттәрендә лә күренә. Шулай, Карл Йохан Мальмстен, Жак Филипп Мари Биненың беренсе формулаһына оҡшаш формула сығарған[4]
ә Матиах Лерх ошондай күренештәге бөтә интегралдарҙың да
гамма-функцияның логарифмдарына ҡайтып ҡалыуын күрһәткән. Айырып әйткәндә, Биненың икенсе формулаһына оҡшаш формула түбәндәге күренештә:
- (40-сы күнегеүҙе ҡара[5])
Бынан тыш, Карл Йохан Мальмстен шулай уҡ гамма-функцияның логарифмы өсөн бер нисә интеграль формула сығарған, унда интеграл аҫты аңлатмаһында логарифмлы гиперболик функциялар бар (йәки шул уҡ полиномамлы логарифм логарифмы). Айырып әйткәндә,
- (см. упр. 2, 29-h, 30 в[5])
Ярослав Благушин рациональ аргументы өсөн, бында һәм ыңғай бөтөн һандар, һәм -дан ҙур түгел, түбәндәге формулаларҙың дөрөҫ булыуын күрһәткән:
Улай ғына түгел, интеграл аҫты аңлатмаһында логарифмлы гиперболик функциялар (йәки арктангенс) ингән интегралдар дөйөм осраҡта, йыш ҡына гамма-функцияның логарифмына һәм уның сығарылмаһына (полигамма-функция) ҡайтып ҡалалар, шул иҫәптән комплекслы аргументлы, мәҫәлән 4-b, 7-а и 13-b күнегеүҙәрен ҡара[5].
Гамма-функция логарифмы шулай уҡ дөйөмләштерелгән дзета-функцияның аналитик дауамы менән тығыҙ бәйләнгән
Лерх Матиаш Лерх сығарған был мөһим бәйләнеш,дөйөмләштерелгән дзета функция өсөн билдәле формулалар аша гамма-функцияның логарифмы өсөн күп һанда интеграль күренештәр алырға мөмкинлек бирә.
Гамма-функция логарифмы өсөн Фурье рәте түбәндәге күренештә
Был формуланы ғәҙәттә, уны 1847 йылда сығарған Эрнст Куммерҙыҡы тип һанайҙар, (авторитетлы әҙәбиәттә[4][7][8] был рәтте хатта гамма-функция логарифмы өсөн Куммер рәте тип атайҙар). Ләкин күптән түгел был формуланың Карл Мальмстен тарафынан 1842 йылда уҡ сығарылғанлығы асыҡлана (ҡара. Ярослав Благушин[5]).
Фурье рәтенә тарҡалмаһынан тыш, башҡа рәттәргә лә тарҡалмаһы бар. Киң билдәлеләрҙән Джеймс Стирлинг рәте
Уның стандарт вариацияһында
бында коэффициенттары Бернулли һандарын аңлата.
Вейерштрасс буйынса гамма-функция билдәләмәһенән рәт менән тағы бер мөһим формула килеп сыға[9]
- .
Айырым ҡиммәттәре
[үҙгәртергә | сығанаҡты үҙгәртеү]Бөтөн һәм ярым бөтөн аргументтарҙың гамма-функциялары элементар функциялар аша күрһәтелә. Айырып әйткәндә
Гамма-функцияның 1/4 и 1/3 нөктәләрендә ҡиммәттәрен эҙләү Эйлер, Гаусс һәм Лежандрҙың ентекле эҙләнеү объекты булып тора, әммә уларға был ҡиммәттәрҙе йомоҡ күренештә иҫәпләү насип булмай[10].
Γ(1/4) өсөн йомоҡ күренештә түбәндәге күҙаллауҙар бар
бында AGM — арифметик-геометрик урта функция, G — Каталан даимиһы һәм A — Глейшер—Кинкелин даимиһы.
Дөйөмләштреү
[үҙгәртергә | сығанаҡты үҙгәртеү]Гамма-функцияның классик интеграль билдәләмәһендә интеграллау сиктәре билдәләп ҡуйылған. Шулай уҡ тулы булмаған гамма-функцияны ҡарайҙар, ул өҫкө йәки аҫҡы интеграллау сиге үҙгәреүсәнле шундай уҡ интеграл менән билдәләнә. Өҫкө тулы булмаған гамма-функцияны айырып ҡарайҙар, йыш ҡына ике үҙгәреүсәнле гамма-функция итеп тамғалайҙар:
һәм аҫҡы тулы булмаған гамма-функцияны айырып ҡарайҙар, оҡшаш рәүештә «гамма» бәләкәй хәреф менән тамғалана:
- .
Ҡайһы беерҙә тулы булмаған гамма функцияны ошолай билдәләйҙәр[11]:
- .
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ https://scholarlycommons.pacific.edu/euler-works/19/
- ↑ http://dlmf.nist.gov/5.2.E1
- ↑ 2-20.2 // ISO 80000-2:2019Quantities and units — Part 2: Mathematics — 2 — Халыҡ-ара стандартлаштырыу ойошмаһы, 2019. — 36 с.
- ↑ 4,0 4,1 4,2 Harry Bateman and Arthur Erdélyi Higher Transcendental Functions [in 3 volumes]. Mc Graw-Hill Book Company, 1955.
- ↑ 5,0 5,1 5,2 5,3 5,4 Iaroslav V. Blagouchine Rediscovery of Malmsten’s integrals, their evaluation by contour integration methods and some related results. The Ramanujan Journal, vol. 35, no. 1, pp. 21-110, 2014. PDF
- ↑ Iaroslav V. Blagouchine A theorem for the closed-form evaluation of the first generalized Stieltjes constant at rational arguments and some related summations Journal of Number Theory (Elsevier), vol. 148, pp. 537—592, 2015.
- ↑ E.T. Whittaker and G. N. Watson A course of modern analysis. An introduction to the general theory of infinite processes and of analytic functions, with an account of the principal transcendental functions (third edition). Cambridge at the University Press, 1920.
- ↑ H.M. Srivastava and J. Choi Series Associated with the Zeta and Related Functions. Kluwer Academic Publishers. The Netherlands, 2001
- ↑ Д. С. Кузнецов. Специальные функции (2-е изд.). Высшая Школа, Москва, 1965.
- ↑ Philip J. Davis Leonhard Euler’s Integral: A Historical Profile of the Gamma-Function. American Mathematical Monthly, vol. 66, pp. 849—869, 1959.
- ↑ [{{{ссылка}}} Неполная гамма-функция] — Математической энциклопедии
Әҙәбиәт һәм һылтанмалар
[үҙгәртергә | сығанаҡты үҙгәртеү]- В. Я. Арсенин. Математическая физика: основные уравнения и специальные функции, глава X, сс. 225—233. Наука, Москва, 1966.
- М. А. Евграфов. Аналитические функции, глава VI, сс. 267—273. Наука, Москва, 1968.
- М. А. Евграфов и др. Сборник задач по теории аналитических функций, сс. 307—316. Наука, Москва, 1969.
- Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления (7-е изд.), глава XIV, сс. 750—794. Наука, Москва, 1969.
- А. И. Маркушевич. Теория аналитических функций (2-е изд.), том 2, сс. 303—324. Наука, Москва, 1968.
- Н. Н. Лебедев. Специальные функции и их приложения (2-е изд.), глава I, сс. 11—27. ФМ, Москва, 1963.
- А. Ф. Никифоров и В. Б. Уваров. Специальные функции математической физики, сс. 263—268. Наука, Москва, 1978.
- R. Campbell. Les intégrales eulériennes et leurs applications, Dunod, Paris, 1966.
- M. Godefroy. La fonction Gamma; Théorie, Histoire, Bibliographie, Gauthier-Villars, Paris, 1901.
- E. Artin. Einführung in die Theorie der Gammafunktion, Teubner, Leipzig, 1931.
- N. Nielson. Handbuch der Theorie der Gammafunktion, Teubner, Leipzig, 1906.
Шулай уҡ ҡарағыҙ
[үҙгәртергә | сығанаҡты үҙгәртеү]- Леонард Эйлер хөрмәтенә аталған объекттар исемлеге
- K-функция
- G-функция Барнса
- Бета-функция
- Гамма-распределение
- Неполная гамма-функция


















![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)




















![{\displaystyle \ln \Gamma (z)\,=\,\left(z-{\frac {1}{\,2\,}}\right)\!\ln z-z+{\frac {1}{\,2\,}}\ln 2\pi +\!\int \limits _{0}^{\,\infty }\!\left[{\frac {1}{e^{x}-1}}-{\frac {1}{x}}+{\frac {1}{2}}\right]{\frac {e^{-xz}}{x}}\,dx\,,\qquad \operatorname {Re} {z}>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df864503548a1791eb140937f35e0d52a57c343c)

![{\displaystyle \ln \Gamma (z)\,=\int \limits _{0}^{\,\infty }\!\left[z-1-{\frac {1-e^{-(z-1)x}}{1-e^{-x}}}\right]{\frac {e^{-x}}{x}}\,dx\,,\qquad \operatorname {Re} {z}>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad3d237379e6709aa85b891429a336782764a553)

![{\displaystyle \ln \Gamma (z)=-{\biggl (}z-{\frac {1}{2}}{\biggr )}\cdot \left\{1-\ln {\biggl (}z-{\frac {1}{2}}{\biggr )}\!\right\}+{\frac {1}{2}}\ln 2\pi -\,2\!\int \limits _{0}^{\infty }\!{\frac {\operatorname {arctg} {\big [}x/{\big (}z-{\tfrac {1}{2}}{\big )}{\big ]}}{e^{2\pi x}+1}}\,dx,\qquad \operatorname {Re} {z}>{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261a38ceb69f2a1f7ec2ac10043af6fd0df13387)










![{\displaystyle \ln \Gamma (z)=-\gamma z-\ln z+\sum _{n=1}^{\infty }\left[{\frac {z}{n}}-\ln \!\left(1+{\frac {z}{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d0430719756d45b5685a3b39a52146ab0861c96)











![{\displaystyle \Gamma \left({\tfrac {1}{2}}+n\right)={(2n)! \over 4^{n}n!}{\sqrt {\pi }}={\frac {(2n-1)!!}{2^{n}}}\,{\sqrt {\pi }}={\sqrt {\pi }}\cdot \left[{n-{\frac {1}{2}} \choose n}n!\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0294ff50833fe87162a25b3d82270f486b02037a)
![{\displaystyle \Gamma \left({\tfrac {1}{2}}-n\right)={(-4)^{n}n! \over (2n)!}{\sqrt {\pi }}={\frac {(-2)^{n}}{(2n-1)!!}}\,{\sqrt {\pi }}={\sqrt {\pi }}/\left[{-{\frac {1}{2}} \choose n}n!\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/060544c7ae8004048b00950cd465151cdaf93261)





