Рис. 1 синустың косинустың тангенстың котангенстың секанстың косеканстың Тригонометри́к фу́нкциялар — элементар функциялар , улар тарихи рәүештә тура мөйөшлө өсмөйөштәрҙе ҡарағанда барлыҡҡа килгәндәр һәм был өсмөйөштәрҙең яҡтары оҙонлоғоноң гипотенуза эргәһендәге ҡыҫынҡы мөйөштәренә бәйлелеген күрһәтәләр (йәки, шуға тиң мәғәнәлә, түңәрәктә хордаларҙың һәм бейеклектәрҙең дуғаның үҙәк мөйөшөнә бәйлелеге. Был функциялар фәндең төрлө өлкәләрендә бик киң ҡулланыу таптылар. Артабан тригонометрик функцяларҙың билдәләмәләре киңәйтелә, хәҙер уларҙың аргументы булып теләһә ниндәй ысын һан йәки хатта комплекслы һан торорға мөмкин. Тригонометрик функцияларҙың үҙсәнлектәрен өйрәнеүсе фән тригонометрия тип атала.
Тригонометрик функцияларға инәләр:
тура тригонометрик функциялар синус (
sin
x
{\displaystyle \sin x}
косинус (
cos
x
{\displaystyle \cos x}
тригонометрик функцияларҙың сығарылмалары тангенс (
t
g
x
{\displaystyle \mathrm {tg} \,x}
котангенс (
c
t
g
x
{\displaystyle \mathrm {ctg} \,x}
башҡа тригонометрик функциялар секанс (
sec
x
{\displaystyle \sec x}
косеканс (
c
o
s
e
c
x
{\displaystyle \mathrm {cosec} \,x}
Инглиз һәм америка әҙәбиәтендә тангенс, котангенс һәм косеканс
tan
x
,
cot
x
,
csc
x
{\displaystyle \tan x,\cot x,\csc x}
[ 1]
Был алты функциянан тыш һирәк ҡулланылған тригонометрик функциялар бар (версинус һ.б.), шулай уҡ кире тригонометрик функциялар (арксинус, арккосинус һ.б.), улар айырым мәҡәләләрҙә ҡарала.
Ысын аргументтың синусы һәм косинусы периодлы, өҙлөкһөҙ һәм сикһеҙ дифференциалланыусы, ҡиммәттәре ысын һандар булған функциялар. Ҡалған дүрт функция ысын һандар күмәклегендә шулай уҡ периодлы, билдәләнеү өлкәһендә сикһеҙ дифференциалланыусы,ҡиммәттәре ысын һандар булған функциялар, ләкин өҙлөкһөҙ түгелдәр. Тангенс һәм секанстың
±
π
n
+
π
2
{\displaystyle \pm \pi n+{\frac {\pi }{2}}}
±
π
n
{\displaystyle \pm \pi n}
Рис. 2 Рис. 3
α
{\displaystyle \alpha }
Ғәҙәттә тригонометрик функциялар геометрик билдәләнәләр[ 2] декарт координаталар системаһы бирелһен, ти. Радиусы
R
{\displaystyle R}
O
{\displaystyle O}
O
B
{\displaystyle OB}
B
{\displaystyle B}
x
B
{\displaystyle x_{B}}
ординатаһын
y
B
{\displaystyle y_{B}}
Синус тип
sin
α
=
y
B
R
.
{\displaystyle \sin \alpha ={\frac {y_{B}}{R}}.}
Косинус тип
cos
α
=
x
B
R
.
{\displaystyle \cos \alpha ={\frac {x_{B}}{R}}.}
Тангенс
tg
α
=
sin
α
cos
α
=
y
B
x
B
.
{\displaystyle \operatorname {tg} \alpha ={\frac {\sin \alpha }{\cos \alpha }}={\frac {y_{B}}{x_{B}}}.}
Котангенс
ctg
α
=
cos
α
sin
α
=
x
B
y
B
.
{\displaystyle \operatorname {ctg} \alpha ={\frac {\cos \alpha }{\sin \alpha }}={\frac {x_{B}}{y_{B}}}.}
Секанс
sec
α
=
1
cos
α
=
R
x
B
.
{\displaystyle \sec \alpha ={\frac {1}{\cos \alpha }}={\frac {R}{x_{B}}}.}
Косеканс
cosec
α
=
1
sin
α
=
R
y
B
.
{\displaystyle \operatorname {cosec} \alpha ={\frac {1}{\sin \alpha }}={\frac {R}{y_{B}}}.}
Тригонометрик функцияларҙың ҡиммәттәре әйләнәнең
R
{\displaystyle R}
y
B
{\displaystyle y_{B}}
x
B
{\displaystyle x_{B}}
Әгәр
α
{\displaystyle \alpha }
ысын һан булһа, ул саҡта математик анализда
α
{\displaystyle \alpha }
радиан үлсәме
α
{\displaystyle \alpha }
Рис. 4 Геометрияның мәктәп курсында ҡыҫынҡы мөйөштөң тригонометрик функциялары тура мөйөшлө өсмөйөштөң яҡтарының сағыштырмаһы булараҡ билдәләнә.
[ 3] OAB α . Шулай итеп:
α
{\displaystyle \alpha }
A
B
O
B
{\displaystyle {\frac {AB}{OB}}}
катеттың гипотенузаға сағыштырмаһы).
α
{\displaystyle \alpha }
O
A
O
B
{\displaystyle {\frac {OA}{OB}}}
катеттың гипотенузаға сағыштырмаһы).ом угла
α
{\displaystyle \alpha }
A
B
O
A
{\displaystyle {\frac {AB}{OA}}}
катеттың теркәлгән катетҡа сағыштырмаһы).
α
{\displaystyle \alpha }
O
A
A
B
{\displaystyle {\frac {OA}{AB}}}
катеттың ҡаршы ятыусы катетҡа сағыштырмаһы).
α
{\displaystyle \alpha }
O
B
O
A
{\displaystyle {\frac {OB}{OA}}}
гипотенузаның теркәлгән катетҡа сағыштырмаһы).
α
{\displaystyle \alpha }
O
B
A
B
{\displaystyle {\frac {OB}{AB}}}
гипотенузаның ҡаршы ятыусы катетҡа сағыштырмаһы).Башы
O
{\displaystyle O}
O
A
{\displaystyle OA}
гипотенузаға тигеҙ булған әйләнә төҙөп, функцияларҙың был билдәләмәләре бынан алдағы кеүек үк һөҙөмтәгә килтереүен күрергә була.
Был билдәләмә бер ни тиклем методик өҫтөнлөккә эйә, сөнки координаталар системаһы индереүҙе талап итмәй, ләкин шулай уҡ ҙур етешһеҙлеге бар, сөнки йәйенке мөйөшлө өсмөйөштәр тураһында элементар мәсьәләләрҙе сисеү өсөн дә белергә кәрәк булған хатта йәйенке мөйөштәр өсөн дә тригонометрик функцияларға билдәләмә биреп булмай. (ҡара: Теорема синусов , Теорема косинусов ).
Тригонометрик функциялар синус, косинус, секанс һәм косеканс
2
π
(
360
∘
)
{\displaystyle 2\pi ~(360^{\circ })}
π
(
180
∘
)
{\displaystyle \pi ~(180^{\circ })}
периодлы функциялар.
Теләһә ниндәй мөйөштөң тригонометрик функцияларын, уларҙың периодлы булыуын һәм килтереү формулаларын ҡулланып, ҡыҫынҡы мөйөштөң тригонометрик функцияларына ҡайтарып ҡалдырып була.
Был, мәҫәлән, таблицалар буйынса тригонометрик функцияларҙың ҡиммәттәрен табыу өсөн кәрәк, сөнки таблицаларҙа ғәҙәттә тик ҡыҫынҡы мөйөштәр өсөн генә ҡиммәттәр бирелә.
Косинус һәм синус функцияларына, косинус өсөн
R
(
0
)
=
1
{\displaystyle R(0)=1}
R
′
(
0
)
=
1
{\displaystyle R'(0)=1}
d
2
d
φ
2
R
(
φ
)
=
−
R
(
φ
)
,
{\displaystyle {\frac {d^{2}}{d\varphi ^{2}}}R(\varphi )=-R(\varphi ),}
дифференциаль тигеҙләмәһенең йоп (косинус) һәм таҡ (синус) сығарылышы булараҡ, йәғни икенсе сығарылмалары минус тамғаһы менән алынған функцияның үҙенә тигеҙ булған, бер үҙгәреүсәнле функция булараҡ, билдәләмә бирергә була:
(
cos
x
)
″
=
−
cos
x
,
{\displaystyle \ \left(\cos x\right)''=-\cos x,}
(
sin
x
)
″
=
−
sin
x
.
{\displaystyle \ \left(\sin x\right)''=-\sin x.}
Косинус һәм синус функцияларына (ярашлы рәүештә
f
{\displaystyle f}
g
{\displaystyle g}
[ 4]
0
<
x
<
π
/
2
{\displaystyle 0<x<\pi /2}
f
(
x
)
2
+
g
(
x
)
2
=
1
,
{\displaystyle f(x)^{2}+g(x)^{2}=1,}
g
(
π
/
2
)
=
1
,
{\displaystyle g(\pi /2)=1,}
0
<
g
(
x
)
<
1
{\displaystyle 0<g(x)<1}
түбәндәге функциональ тигеҙләмәләр системаһының сығарылышы булараҡ билдәләмә бирергә була:
{
f
(
x
+
y
)
=
f
(
x
)
f
(
y
)
−
g
(
x
)
g
(
y
)
g
(
x
+
y
)
=
g
(
x
)
f
(
y
)
+
f
(
x
)
g
(
y
)
{\displaystyle \left\{{\begin{array}{rcl}f(x+y)&=&f(x)f(y)-g(x)g(y)\\g(x+y)&=&g(x)f(y)+f(x)g(y)\end{array}}\right.}
Геометрияны һәм сикләмәләрҙең үҙсәнлектәрен файҙаланып, синустың сығарылмаһы косинусҡа тигеҙ һәм косинустың сығарылмаһы минус синусҡа тигеҙ булыуын иҫбат итергә мөмкин. Ул саҡта Тейлор рәте теорияһын ҡулланырға һәм синус менән косинусты дәрәжәле рәттәр рәүешендә күрһәтергә мөмкин:
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
x
9
9
!
−
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
+
1
(
2
n
+
1
)
!
,
{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{9}}{9!}}-\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},}
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
x
8
8
!
−
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
(
2
n
)
!
.
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+{\frac {x^{8}}{8!}}-\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.}
Ошо формулаларҙы, шулай уҡ
tg
x
=
sin
x
cos
x
,
{\displaystyle \operatorname {tg} \,x={\frac {\sin x}{\cos x}},}
ctg
x
=
cos
x
sin
x
,
{\displaystyle \operatorname {ctg} \,x={\frac {\cos x}{\sin x}},}
sec
x
=
1
cos
x
{\displaystyle \sec x={\frac {1}{\cos x}}}
cosec
x
=
1
sin
x
,
{\displaystyle \operatorname {cosec} \,x={\frac {1}{\sin x}},}
tg
x
=
x
+
1
3
x
3
+
2
15
x
5
+
17
315
x
7
+
62
2835
x
9
+
⋯
=
∑
n
=
1
∞
2
2
n
(
2
2
n
−
1
)
|
B
2
n
|
(
2
n
)
!
x
2
n
−
1
(
−
π
2
<
x
<
π
2
)
,
{\displaystyle {\operatorname {tg} \,x=x+{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}+{\frac {17}{315}}\,x^{7}+{\frac {62}{2835}}\,x^{9}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}}x^{2n-1}\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}
ctg
x
=
1
x
−
x
3
−
x
3
45
−
2
x
5
945
−
x
7
4725
−
⋯
=
1
x
−
∑
n
=
1
∞
2
2
n
|
B
2
n
|
(
2
n
)
!
x
2
n
−
1
(
−
π
<
x
<
π
)
,
{\displaystyle {\operatorname {ctg} \,x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-{\frac {x^{7}}{4725}}-\cdots ={\frac {1}{x}}-\sum _{n=1}^{\infty }{\frac {2^{2n}|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),}}
sec
x
=
1
+
1
2
x
2
+
5
24
x
4
+
61
720
x
6
+
277
8064
x
8
+
⋯
=
∑
n
=
0
∞
|
E
n
|
(
2
n
)
!
x
2
n
,
(
−
π
2
<
x
<
π
2
)
,
{\displaystyle {\sec x=1+{\frac {1}{2}}\,x^{2}+{\frac {5}{24}}\,x^{4}+{\frac {61}{720}}\,x^{6}+{\frac {277}{8064}}\,x^{8}+\cdots =\sum _{n=0}^{\infty }{\frac {|E_{n}|}{(2n)!}}\,x^{2n},\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}
cosec
x
=
1
x
+
1
6
x
+
7
360
x
3
+
31
15120
x
5
+
127
604800
x
7
+
⋯
=
1
x
+
∑
n
=
1
∞
2
(
2
2
n
−
1
−
1
)
|
B
2
n
|
(
2
n
)
!
x
2
n
−
1
(
−
π
<
x
<
π
)
,
{\displaystyle \operatorname {cosec} x={\frac {1}{x}}+{\frac {1}{6}}\,x+{\frac {7}{360}}\,x^{3}+{\frac {31}{15120}}\,x^{5}+{\frac {127}{604800}}\,x^{7}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(2^{2n-1}-1)|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),}
бында
B
n
{\displaystyle B_{n}}
Бернулли һандары ,
E
n
{\displaystyle E_{n}}
Эйлер һандары .Тригонометрик функциялар күпбыуындарҙың сикһеҙ ҡабатландығы рәүешендә лә күрһәтелергә мөмкин.
sin
x
=
x
∏
n
=
1
∞
(
1
−
x
2
π
2
n
2
)
{\displaystyle \sin x=x\,\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)}
cos
x
=
∏
n
=
0
∞
(
1
−
4
x
2
π
2
(
2
n
+
1
)
2
)
{\displaystyle \cos x=\prod _{n=0}^{\infty }\left(1-{\frac {4x^{2}}{\pi ^{2}(2n+1)^{2}}}\right)}
Был бәйләнештәр
x
{\displaystyle x}
t
g
x
=
x
1
−
x
2
3
−
x
2
5
−
x
2
7
−
x
2
⋱
.
{\displaystyle \mathop {\rm {tg}} x={\frac {x}{1-{\frac {x^{2}}{3-{\frac {x^{2}}{5-{\frac {x^{2}}{7-{\frac {x^{2}}{\ddots }}}}}}}}}}.}
Бөтә тригонометрик функциялар ҙа бөтә билдәләнеү өлкәһендә өҙлөкһөҙ һәм сикһеҙ дифференциалланыусы:
(
sin
x
)
′
=
cos
x
,
{\displaystyle (\sin x)'=\cos x\,,}
(
cos
x
)
′
=
−
sin
x
,
{\displaystyle (\cos x)'=-\sin x\,,}
(
tg
x
)
′
=
1
cos
2
x
=
1
+
tg
2
x
,
{\displaystyle (\mathop {\operatorname {tg} } x)'={\frac {1}{\cos ^{2}x}}=1+\mathop {\operatorname {tg} } \nolimits ^{2}x,}
(
ctg
x
)
′
=
−
1
sin
2
x
,
{\displaystyle (\mathop {\operatorname {ctg} } \,x)'=-{\frac {1}{\sin ^{2}x}},}
(
sec
x
)
′
=
sin
x
cos
2
x
,
{\displaystyle (\sec x)'={\frac {\sin x}{\cos ^{2}x}},}
(
cosec
x
)
′
=
−
cos
x
sin
2
x
.
{\displaystyle (\operatorname {cosec} ~x)'=-{\frac {\cos x}{\sin ^{2}x}}.}
Тригонометрик функцияларҙың интегралдары билдәләнеү өлкәһендә түбәндәгесә элементар функциялар аша күрһәтеләләр[ 5]
∫
sin
x
d
x
=
−
cos
x
+
C
,
{\displaystyle \int \sin x\,dx=-\cos x+C\,,}
∫
cos
x
d
x
=
sin
x
+
C
,
{\displaystyle \int \cos x\,dx=\sin x+C\,,}
∫
tg
x
d
x
=
−
ln
|
cos
x
|
+
C
,
{\displaystyle \int \mathop {\operatorname {tg} } \,x\,dx=-\ln \left|\cos x\right|+C\,,}
∫
ctg
x
d
x
=
ln
|
sin
x
|
+
C
,
{\displaystyle \int \mathop {\operatorname {ctg} } \,x\,dx=\ln \left|\sin x\right|+C\,,}
∫
sec
x
d
x
=
ln
|
tg
(
π
4
+
x
2
)
|
+
C
,
{\displaystyle \int \sec x\,dx=\ln \left|\operatorname {tg} \,\left({\frac {\pi }{4}}+{\frac {x}{2}}\right)\right|+C\,,}
∫
cosec
x
d
x
=
ln
|
tg
x
2
|
+
C
.
{\displaystyle \int \operatorname {cosec} ~x\,dx=\ln \left|\operatorname {tg} \,{\frac {x}{2}}\right|+C.}
Ҡайһы бер мөйөштәр өсөн синустың, косинус, тангенс, котангенс, секанс һәм косеканстың ҡиммәттәре таблицала килтерелгән. («∞» тамғаһы, функцияның был нөктәлә билдәләнмәгәнлеген, ә уның эргә тирәһендә сикһеҙлеккә ынтылыуын аңлата).
Әйләнәлә косинус һәм синустың ҡиммәттәре.
α
{\displaystyle \alpha }
0
=
0
∘
{\displaystyle 0=0^{\circ }}
π
6
=
30
∘
{\displaystyle {\frac {\pi }{6}}=30^{\circ }}
π
4
=
45
∘
{\displaystyle {\frac {\pi }{4}}=45^{\circ }}
π
3
=
60
∘
{\displaystyle {\frac {\pi }{3}}=60^{\circ }}
π
2
=
90
∘
{\displaystyle {\frac {\pi }{2}}=90^{\circ }}
π
=
180
∘
{\displaystyle \pi =180^{\circ }}
3
π
2
=
270
∘
{\displaystyle {\frac {3\pi }{2}}=270^{\circ }}
2
π
=
360
∘
{\displaystyle 2\pi =360^{\circ }}
sin
α
{\displaystyle \sin \alpha }
0
{\displaystyle 0}
1
2
{\displaystyle {\frac {1}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
1
{\displaystyle 1}
0
{\displaystyle 0}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
cos
α
{\displaystyle \cos \alpha }
1
{\displaystyle 1}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
0
{\displaystyle 0}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
1
{\displaystyle 1}
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
0
{\displaystyle 0}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
1
{\displaystyle 1}
3
{\displaystyle {\sqrt {3}}}
∞
{\displaystyle \infty }
0
{\displaystyle 0}
∞
{\displaystyle \infty }
0
{\displaystyle 0}
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
∞
{\displaystyle \infty }
3
{\displaystyle {\sqrt {3}}}
1
{\displaystyle 1}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
0
{\displaystyle 0}
∞
{\displaystyle \infty }
0
{\displaystyle 0}
∞
{\displaystyle \infty }
sec
α
{\displaystyle \sec \alpha }
1
{\displaystyle 1}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle 2}
∞
{\displaystyle \infty }
−
1
{\displaystyle -1}
∞
{\displaystyle \infty }
1
{\displaystyle 1}
cosec
α
{\displaystyle \operatorname {cosec} \,\alpha }
∞
{\displaystyle \infty }
2
{\displaystyle 2}
2
{\displaystyle {\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
1
{\displaystyle 1}
∞
{\displaystyle \infty }
−
1
{\displaystyle -1}
∞
{\displaystyle \infty }
α
{\displaystyle \alpha }
2
π
3
=
120
∘
{\displaystyle {\frac {2\pi }{3}}=120^{\circ }}
3
π
4
=
135
∘
{\displaystyle {\frac {3\pi }{4}}=135^{\circ }}
5
π
6
=
150
∘
{\displaystyle {\frac {5\pi }{6}}=150^{\circ }}
7
π
6
=
210
∘
{\displaystyle {\frac {7\pi }{6}}=210^{\circ }}
5
π
4
=
225
∘
{\displaystyle {\frac {5\pi }{4}}=225^{\circ }}
4
π
3
=
240
∘
{\displaystyle {\frac {4\pi }{3}}=240^{\circ }}
5
π
3
=
300
∘
{\displaystyle {\frac {5\pi }{3}}=300^{\circ }}
7
π
4
=
315
∘
{\displaystyle {\frac {7\pi }{4}}=315^{\circ }}
11
π
6
=
330
∘
{\displaystyle {\frac {11\pi }{6}}=330^{\circ }}
sin
α
{\displaystyle \sin \alpha }
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
−
1
2
{\displaystyle -{\frac {1}{2}}}
−
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
−
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
−
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
−
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
−
1
2
{\displaystyle -{\frac {1}{2}}}
cos
α
{\displaystyle \cos \alpha }
−
1
2
{\displaystyle -{\frac {1}{2}}}
−
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
−
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
−
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
−
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
−
1
2
{\displaystyle -{\frac {1}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
−
3
{\displaystyle -{\sqrt {3}}}
−
1
{\displaystyle -1}
−
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
1
{\displaystyle 1}
3
{\displaystyle {\sqrt {3}}}
−
3
{\displaystyle -{\sqrt {3}}}
−
1
{\displaystyle -1}
−
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
−
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
−
1
{\displaystyle -1}
−
3
{\displaystyle -{\sqrt {3}}}
3
{\displaystyle {\sqrt {3}}}
1
{\displaystyle 1}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
−
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
−
1
{\displaystyle -1}
−
3
{\displaystyle -{\sqrt {3}}}
sec
α
{\displaystyle \sec \alpha }
−
2
{\displaystyle -2}
−
2
{\displaystyle -{\sqrt {2}}}
−
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
−
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
−
2
{\displaystyle -{\sqrt {2}}}
−
2
{\displaystyle -2}
2
{\displaystyle 2}
2
{\displaystyle {\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
cosec
α
{\displaystyle \operatorname {cosec} \,\alpha }
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle 2}
−
2
{\displaystyle -2}
−
2
{\displaystyle -{\sqrt {2}}}
−
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
−
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
−
2
{\displaystyle -{\sqrt {2}}}
−
2
{\displaystyle -2}
α
{\displaystyle \alpha }
π
12
=
15
∘
{\displaystyle {\frac {\pi }{12}}=15^{\circ }}
π
10
=
18
∘
{\displaystyle {\frac {\pi }{10}}=18^{\circ }}
π
8
=
22
,
5
∘
{\displaystyle {\frac {\pi }{8}}=22{,}5^{\circ }}
π
5
=
36
∘
{\displaystyle {\frac {\pi }{5}}=36^{\circ }}
3
π
10
=
54
∘
{\displaystyle {\frac {3\pi }{10}}=54^{\circ }}
3
π
8
=
67
,
5
∘
{\displaystyle {\frac {3\pi }{8}}=67{,}5^{\circ }}
2
π
5
=
72
∘
{\displaystyle {\frac {2\pi }{5}}=72^{\circ }}
5
π
12
=
75
∘
{\displaystyle {\frac {5\pi }{12}}=75^{\circ }}
sin
α
{\displaystyle \sin \alpha }
2
−
3
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {3}}}}{2}}}
5
−
1
4
{\displaystyle {\frac {{\sqrt {5}}-1}{4}}}
2
−
2
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}
10
−
2
5
4
{\displaystyle {\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}
5
+
1
4
{\displaystyle {\frac {{\sqrt {5}}+1}{4}}}
2
+
2
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}
10
+
2
5
4
{\displaystyle {\frac {\sqrt {10+2{\sqrt {5}}}}{4}}}
2
+
3
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {3}}}}{2}}}
cos
α
{\displaystyle \cos \alpha }
2
+
3
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {3}}}}{2}}}
10
+
2
5
4
{\displaystyle {\frac {\sqrt {10+2{\sqrt {5}}}}{4}}}
2
+
2
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}
5
+
1
4
{\displaystyle {\frac {{\sqrt {5}}+1}{4}}}
10
−
2
5
4
{\displaystyle {\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}
2
−
2
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}
5
−
1
4
{\displaystyle {\frac {{\sqrt {5}}-1}{4}}}
2
−
3
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {3}}}}{2}}}
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
2
−
3
{\displaystyle 2-{\sqrt {3}}}
25
−
10
5
5
{\displaystyle {\frac {\sqrt {25-10{\sqrt {5}}}}{5}}}
2
−
1
{\displaystyle {\sqrt {2}}-1}
5
−
2
5
{\displaystyle {\sqrt {5-2{\sqrt {5}}}}}
25
+
10
5
5
{\displaystyle {\frac {\sqrt {25+10{\sqrt {5}}}}{5}}}
2
+
1
{\displaystyle {\sqrt {2}}+1}
5
+
2
5
{\displaystyle {\sqrt {5+2{\sqrt {5}}}}}
2
+
3
{\displaystyle 2+{\sqrt {3}}}
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
2
+
3
{\displaystyle 2+{\sqrt {3}}}
5
+
2
5
{\displaystyle {\sqrt {5+2{\sqrt {5}}}}}
2
+
1
{\displaystyle {\sqrt {2}}+1}
25
+
10
5
5
{\displaystyle {\frac {\sqrt {25+10{\sqrt {5}}}}{5}}}
5
−
2
5
{\displaystyle {\sqrt {5-2{\sqrt {5}}}}}
2
−
1
{\displaystyle {\sqrt {2}}-1}
25
−
10
5
5
{\displaystyle {\frac {\sqrt {25-10{\sqrt {5}}}}{5}}}
2
−
3
{\displaystyle 2-{\sqrt {3}}}
sec
α
{\displaystyle \sec \alpha }
2
2
−
3
{\displaystyle 2{\sqrt {2-{\sqrt {3}}}}}
50
−
10
5
5
{\displaystyle {\frac {\sqrt {50-10{\sqrt {5}}}}{5}}}
4
−
2
2
{\displaystyle {\sqrt {4-2{\sqrt {2}}}}}
5
−
1
{\displaystyle {\sqrt {5}}-1}
50
+
10
5
5
{\displaystyle {\frac {\sqrt {50+10{\sqrt {5}}}}{5}}}
4
+
2
2
{\displaystyle {\sqrt {4+2{\sqrt {2}}}}}
5
+
1
{\displaystyle {\sqrt {5}}+1}
2
2
+
3
{\displaystyle 2{\sqrt {2+{\sqrt {3}}}}}
cosec
α
{\displaystyle \operatorname {cosec} \,\alpha }
2
2
+
3
{\displaystyle 2{\sqrt {2+{\sqrt {3}}}}}
5
+
1
{\displaystyle {\sqrt {5}}+1}
4
+
2
2
{\displaystyle {\sqrt {4+2{\sqrt {2}}}}}
50
+
10
5
5
{\displaystyle {\frac {\sqrt {50+10{\sqrt {5}}}}{5}}}
5
−
1
{\displaystyle {\sqrt {5}}-1}
4
−
2
2
{\displaystyle {\sqrt {4-2{\sqrt {2}}}}}
50
−
10
5
5
{\displaystyle {\frac {\sqrt {50-10{\sqrt {5}}}}{5}}}
2
2
−
3
{\displaystyle 2{\sqrt {2-{\sqrt {3}}}}}
Ҡайһы бер башҡа мөйөштәр өсөн тригонометрик функцияларҙың ҡиммәттәре
sin
π
60
=
cos
29
π
60
=
sin
3
∘
=
cos
87
∘
=
2
(
3
+
1
)
(
5
−
1
)
−
2
(
3
−
1
)
5
+
5
16
,
{\displaystyle \sin {\frac {\pi }{60}}=\cos {\frac {29\,\pi }{60}}=\sin 3^{\circ }=\cos 87^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}-1)-2({\sqrt {3}}-1){\sqrt {5+{\sqrt {5}}}}}{16}},}
cos
π
60
=
sin
29
π
60
=
cos
3
∘
=
sin
87
∘
=
2
(
3
−
1
)
(
5
−
1
)
+
2
(
3
+
1
)
5
+
5
16
,
{\displaystyle \cos {\frac {\pi }{60}}=\sin {\frac {29\,\pi }{60}}=\cos 3^{\circ }=\sin 87^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}-1)+2({\sqrt {3}}+1){\sqrt {5+{\sqrt {5}}}}}{16}},}
tg
π
60
=
ctg
29
π
60
=
tg
3
∘
=
ctg
87
∘
=
2
(
5
+
2
)
−
3
(
5
+
3
)
+
(
2
−
3
)
(
3
(
5
+
1
)
−
2
)
5
−
2
5
2
,
{\displaystyle \operatorname {tg} {\frac {\pi }{60}}=\operatorname {ctg} {\frac {29\,\pi }{60}}=\operatorname {tg} 3^{\circ }=\operatorname {ctg} 87^{\circ }={\frac {2({\sqrt {5}}+2)-{\sqrt {3}}({\sqrt {5}}+3)+(2-{\sqrt {3}})({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {5-2{\sqrt {5}}}}}{2}},}
ctg
π
60
=
tg
29
π
60
=
ctg
3
∘
=
tg
87
∘
=
2
(
2
(
5
+
2
)
+
3
(
5
+
3
)
)
+
(
3
(
5
−
1
)
+
2
)
2
(
25
+
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{60}}=\operatorname {tg} {\frac {29\,\pi }{60}}=\operatorname {ctg} 3^{\circ }=\operatorname {tg} 87^{\circ }={\frac {2(2({\sqrt {5}}+2)+{\sqrt {3}}({\sqrt {5}}+3))+({\sqrt {3}}({\sqrt {5}}-1)+2){\sqrt {2(25+11{\sqrt {5}})}}}{4}},}
sin
π
30
=
cos
7
π
15
=
sin
6
∘
=
cos
84
∘
=
6
(
5
−
5
)
−
5
−
1
8
,
{\displaystyle \sin {\frac {\pi }{30}}=\cos {\frac {7\,\pi }{15}}=\sin 6^{\circ }=\cos 84^{\circ }={\frac {{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1}{8}},}
cos
π
30
=
sin
7
π
15
=
cos
6
∘
=
sin
84
∘
=
2
(
5
−
5
)
+
3
(
5
+
1
)
8
,
{\displaystyle \cos {\frac {\pi }{30}}=\sin {\frac {7\,\pi }{15}}=\cos 6^{\circ }=\sin 84^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)}{8}},}
tg
π
30
=
ctg
7
π
15
=
tg
6
∘
=
ctg
84
∘
=
2
(
5
−
5
)
−
3
(
5
−
1
)
2
,
{\displaystyle \operatorname {tg} {\frac {\pi }{30}}=\operatorname {ctg} {\frac {7\,\pi }{15}}=\operatorname {tg} 6^{\circ }=\operatorname {ctg} 84^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{2}},}
ctg
π
30
=
tg
7
π
15
=
ctg
6
∘
=
tg
84
∘
=
2
(
25
+
11
5
)
+
3
(
5
+
3
)
2
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{30}}=\operatorname {tg} {\frac {7\,\pi }{15}}=\operatorname {ctg} 6^{\circ }=\operatorname {tg} 84^{\circ }={\frac {{\sqrt {2(25+11{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+3)}{2}},}
sin
π
20
=
cos
9
π
20
=
sin
9
∘
=
cos
81
∘
=
2
(
5
+
1
)
−
2
5
−
5
8
,
{\displaystyle \sin {\frac {\pi }{20}}=\cos {\frac {9\,\pi }{20}}=\sin 9^{\circ }=\cos 81^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)-2{\sqrt {5-{\sqrt {5}}}}}{8}},}
cos
π
20
=
sin
9
π
20
=
cos
9
∘
=
sin
81
∘
=
2
(
5
+
1
)
+
2
5
−
5
8
,
{\displaystyle \cos {\frac {\pi }{20}}=\sin {\frac {9\,\pi }{20}}=\cos 9^{\circ }=\sin 81^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)+2{\sqrt {5-{\sqrt {5}}}}}{8}},}
tg
π
20
=
ctg
9
π
20
=
tg
9
∘
=
ctg
81
∘
=
5
+
1
−
5
+
2
5
,
{\displaystyle \operatorname {tg} {\frac {\pi }{20}}=\operatorname {ctg} {\frac {9\,\pi }{20}}=\operatorname {tg} 9^{\circ }=\operatorname {ctg} 81^{\circ }={{\sqrt {5}}+1-{\sqrt {5+2{\sqrt {5}}}}},}
ctg
π
20
=
tg
9
π
20
=
ctg
9
∘
=
tg
81
∘
=
5
+
1
+
5
+
2
5
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{20}}=\operatorname {tg} {\frac {9\,\pi }{20}}=\operatorname {ctg} 9^{\circ }=\operatorname {tg} 81^{\circ }={{\sqrt {5}}+1+{\sqrt {5+2{\sqrt {5}}}}},}
sin
π
15
=
cos
13
π
30
=
sin
12
∘
=
cos
78
∘
=
2
(
5
+
5
)
−
3
(
5
−
1
)
8
,
{\displaystyle \sin {\frac {\pi }{15}}=\cos {\frac {13\,\pi }{30}}=\sin 12^{\circ }=\cos 78^{\circ }={\frac {{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{8}},}
cos
π
15
=
sin
13
π
30
=
cos
12
∘
=
sin
78
∘
=
6
(
5
+
5
)
+
5
−
1
8
,
{\displaystyle \cos {\frac {\pi }{15}}=\sin {\frac {13\,\pi }{30}}=\cos 12^{\circ }=\sin 78^{\circ }={\frac {{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1}{8}},}
tg
π
15
=
ctg
13
π
30
=
tg
12
∘
=
ctg
78
∘
=
3
(
3
−
5
)
−
2
(
25
−
11
5
)
2
,
{\displaystyle \operatorname {tg} {\frac {\pi }{15}}=\operatorname {ctg} {\frac {13\,\pi }{30}}=\operatorname {tg} 12^{\circ }=\operatorname {ctg} 78^{\circ }={\frac {{\sqrt {3}}(3-{\sqrt {5}})-{\sqrt {2(25-11{\sqrt {5}})}}}{2}},}
ctg
π
15
=
tg
13
π
30
=
ctg
12
∘
=
tg
78
∘
=
3
(
5
+
1
)
+
2
(
5
+
5
)
2
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{15}}=\operatorname {tg} {\frac {13\,\pi }{30}}=\operatorname {ctg} 12^{\circ }=\operatorname {tg} 78^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)+{\sqrt {2(5+{\sqrt {5}})}}}{2}},}
sin
7
π
60
=
cos
23
π
60
=
sin
21
∘
=
cos
69
∘
=
−
2
(
3
−
1
)
(
5
+
1
)
+
2
(
3
+
1
)
5
−
5
16
,
{\displaystyle \sin {\frac {7\,\pi }{60}}=\cos {\frac {23\,\pi }{60}}=\sin 21^{\circ }=\cos 69^{\circ }={\frac {-{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}+1)+2({\sqrt {3}}+1){\sqrt {5-{\sqrt {5}}}}}{16}},}
cos
7
π
60
=
sin
23
π
60
=
cos
21
∘
=
sin
69
∘
=
2
(
3
+
1
)
(
5
+
1
)
+
2
(
3
−
1
)
5
−
5
16
,
{\displaystyle \cos {\frac {7\,\pi }{60}}=\sin {\frac {23\,\pi }{60}}=\cos 21^{\circ }=\sin 69^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}+1)+2({\sqrt {3}}-1){\sqrt {5-{\sqrt {5}}}}}{16}},}
tg
7
π
60
=
ctg
23
π
60
=
tg
21
∘
=
ctg
69
∘
=
2
(
2
(
5
−
2
)
−
3
(
3
−
5
)
)
+
(
3
(
5
+
1
)
−
2
)
2
(
25
−
11
5
)
4
,
{\displaystyle \operatorname {tg} {\frac {7\,\pi }{60}}=\operatorname {ctg} {\frac {23\,\pi }{60}}=\operatorname {tg} 21^{\circ }=\operatorname {ctg} 69^{\circ }={\frac {2(2({\sqrt {5}}-2)-{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
ctg
7
π
60
=
tg
23
π
60
=
ctg
21
∘
=
tg
69
∘
=
2
(
2
(
5
−
2
)
+
3
(
3
−
5
)
)
+
(
3
(
5
+
1
)
+
2
)
2
(
25
−
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {7\,\pi }{60}}=\operatorname {tg} {\frac {23\,\pi }{60}}=\operatorname {ctg} 21^{\circ }=\operatorname {tg} 69^{\circ }={\frac {2(2({\sqrt {5}}-2)+{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)+2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
sin
2
π
15
=
cos
11
π
30
=
sin
24
∘
=
cos
66
∘
=
3
(
5
+
1
)
−
2
(
5
−
5
)
8
,
{\displaystyle \sin {\frac {2\,\pi }{15}}=\cos {\frac {11\,\pi }{30}}=\sin 24^{\circ }=\cos 66^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2(5-{\sqrt {5}})}}}{8}},}
cos
2
π
15
=
sin
11
π
30
=
cos
24
∘
=
sin
66
∘
=
5
+
1
+
6
(
5
−
5
)
8
,
{\displaystyle \cos {\frac {2\,\pi }{15}}=\sin {\frac {11\,\pi }{30}}=\cos 24^{\circ }=\sin 66^{\circ }={\frac {{\sqrt {5}}+1+{\sqrt {6(5-{\sqrt {5}})}}}{8}},}
tg
2
π
15
=
ctg
11
π
30
=
tg
24
∘
=
ctg
66
∘
=
−
3
(
3
+
5
)
+
2
(
25
+
11
5
)
2
,
{\displaystyle \operatorname {tg} {\frac {2\,\pi }{15}}=\operatorname {ctg} {\frac {11\,\pi }{30}}=\operatorname {tg} 24^{\circ }=\operatorname {ctg} 66^{\circ }={\frac {-{\sqrt {3}}(3+{\sqrt {5}})+{\sqrt {2(25+11{\sqrt {5}})}}}{2}},}
ctg
2
π
15
=
tg
11
π
30
=
ctg
24
∘
=
tg
66
∘
=
3
(
5
−
1
)
+
2
(
5
−
5
)
2
,
{\displaystyle \operatorname {ctg} {\frac {2\,\pi }{15}}=\operatorname {tg} {\frac {11\,\pi }{30}}=\operatorname {ctg} 24^{\circ }=\operatorname {tg} 66^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}-1)+{\sqrt {2(5-{\sqrt {5}})}}}{2}},}
sin
3
π
20
=
cos
7
π
20
=
sin
27
∘
=
cos
63
∘
=
−
2
(
5
−
1
)
+
2
5
+
5
8
,
{\displaystyle \sin {\frac {3\,\pi }{20}}=\cos {\frac {7\,\pi }{20}}=\sin 27^{\circ }=\cos 63^{\circ }={\frac {-{\sqrt {2}}({\sqrt {5}}-1)+2{\sqrt {5+{\sqrt {5}}}}}{8}},}
cos
3
π
20
=
sin
7
π
20
=
cos
27
∘
=
sin
63
∘
=
2
(
5
−
1
)
+
2
5
+
5
8
,
{\displaystyle \cos {\frac {3\,\pi }{20}}=\sin {\frac {7\,\pi }{20}}=\cos 27^{\circ }=\sin 63^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}-1)+2{\sqrt {5+{\sqrt {5}}}}}{8}},}
tg
3
π
20
=
ctg
7
π
20
=
tg
27
∘
=
ctg
63
∘
=
5
−
1
−
5
−
2
5
,
{\displaystyle \operatorname {tg} {\frac {3\,\pi }{20}}=\operatorname {ctg} {\frac {7\,\pi }{20}}=\operatorname {tg} 27^{\circ }=\operatorname {ctg} 63^{\circ }={{\sqrt {5}}-1-{\sqrt {5-2{\sqrt {5}}}}},}
ctg
3
π
20
=
tg
7
π
20
=
ctg
27
∘
=
tg
63
∘
=
5
−
1
+
5
−
2
5
,
{\displaystyle \operatorname {ctg} {\frac {3\,\pi }{20}}=\operatorname {tg} {\frac {7\,\pi }{20}}=\operatorname {ctg} 27^{\circ }=\operatorname {tg} 63^{\circ }={{\sqrt {5}}-1+{\sqrt {5-2{\sqrt {5}}}}},}
sin
11
π
60
=
cos
19
π
60
=
sin
33
∘
=
cos
57
∘
=
2
(
3
+
1
)
(
5
−
1
)
+
2
(
3
−
1
)
5
+
5
16
,
{\displaystyle \sin {\frac {11\,\pi }{60}}=\cos {\frac {19\,\pi }{60}}=\sin 33^{\circ }=\cos 57^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}-1)+2({\sqrt {3}}-1){\sqrt {5+{\sqrt {5}}}}}{16}},}
cos
11
π
60
=
sin
19
π
60
=
cos
33
∘
=
sin
57
∘
=
−
2
(
3
−
1
)
(
5
−
1
)
+
2
(
3
+
1
)
5
+
5
16
,
{\displaystyle \cos {\frac {11\,\pi }{60}}=\sin {\frac {19\,\pi }{60}}=\cos 33^{\circ }=\sin 57^{\circ }={\frac {-{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}-1)+2({\sqrt {3}}+1){\sqrt {5+{\sqrt {5}}}}}{16}},}
tg
11
π
60
=
ctg
19
π
60
=
tg
33
∘
=
ctg
57
∘
=
−
2
(
5
+
2
)
+
3
(
3
+
5
)
+
(
2
−
3
)
(
3
(
5
+
1
)
−
2
)
5
−
2
5
2
,
{\displaystyle \operatorname {tg} {\frac {11\,\pi }{60}}=\operatorname {ctg} {\frac {19\,\pi }{60}}=\operatorname {tg} 33^{\circ }=\operatorname {ctg} 57^{\circ }={\frac {-2({\sqrt {5}}+2)+{\sqrt {3}}(3+{\sqrt {5}})+(2-{\sqrt {3}})({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {5-2{\sqrt {5}}}}}{2}},}
ctg
11
π
60
=
tg
19
π
60
=
ctg
33
∘
=
tg
57
∘
=
−
2
(
2
(
5
+
2
)
+
3
(
3
+
5
)
)
+
(
3
(
5
−
1
)
+
2
)
2
(
25
+
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {11\,\pi }{60}}=\operatorname {tg} {\frac {19\,\pi }{60}}=\operatorname {ctg} 33^{\circ }=\operatorname {tg} 57^{\circ }={\frac {-2(2({\sqrt {5}}+2)+{\sqrt {3}}(3+{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}-1)+2){\sqrt {2(25+11{\sqrt {5}})}}}{4}},}
sin
13
π
60
=
cos
17
π
60
=
sin
39
∘
=
cos
51
∘
=
2
(
3
+
1
)
(
5
+
1
)
−
2
(
3
−
1
)
5
−
5
16
,
{\displaystyle \sin {\frac {13\,\pi }{60}}=\cos {\frac {17\,\pi }{60}}=\sin 39^{\circ }=\cos 51^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}+1)-2({\sqrt {3}}-1){\sqrt {5-{\sqrt {5}}}}}{16}},}
cos
13
π
60
=
sin
17
π
60
=
cos
39
∘
=
sin
51
∘
=
2
(
3
−
1
)
(
5
+
1
)
+
2
(
3
+
1
)
5
−
5
16
,
{\displaystyle \cos {\frac {13\,\pi }{60}}=\sin {\frac {17\,\pi }{60}}=\cos 39^{\circ }=\sin 51^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}+1)+2({\sqrt {3}}+1){\sqrt {5-{\sqrt {5}}}}}{16}},}
tg
13
π
60
=
ctg
17
π
60
=
tg
39
∘
=
ctg
51
∘
=
−
2
(
2
(
5
−
2
)
+
3
(
3
−
5
)
)
+
(
3
(
5
+
1
)
+
2
)
2
(
25
−
11
5
)
4
,
{\displaystyle \operatorname {tg} {\frac {13\,\pi }{60}}=\operatorname {ctg} {\frac {17\,\pi }{60}}=\operatorname {tg} 39^{\circ }=\operatorname {ctg} 51^{\circ }={\frac {-2(2({\sqrt {5}}-2)+{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)+2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
ctg
13
π
60
=
tg
17
π
60
=
ctg
39
∘
=
tg
51
∘
=
−
2
(
2
(
5
−
2
)
−
3
(
3
−
5
)
)
+
(
3
(
5
+
1
)
−
2
)
2
(
25
−
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {13\,\pi }{60}}=\operatorname {tg} {\frac {17\,\pi }{60}}=\operatorname {ctg} 39^{\circ }=\operatorname {tg} 51^{\circ }={\frac {-2(2({\sqrt {5}}-2)-{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
sin
7
π
30
=
cos
8
π
30
=
sin
42
∘
=
cos
48
∘
=
−
(
5
−
1
)
+
6
(
5
+
5
)
8
,
{\displaystyle \sin {\frac {7\,\pi }{30}}=\cos {\frac {8\,\pi }{30}}=\sin 42^{\circ }=\cos 48^{\circ }={\frac {-({\sqrt {5}}-1)+{\sqrt {6(5+{\sqrt {5}})}}}{8}},}
cos
7
π
30
=
sin
8
π
30
=
cos
42
∘
=
sin
48
∘
=
3
(
5
−
1
)
+
2
(
5
+
5
)
8
,
{\displaystyle \cos {\frac {7\,\pi }{30}}=\sin {\frac {8\,\pi }{30}}=\cos 42^{\circ }=\sin 48^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}-1)+{\sqrt {2(5+{\sqrt {5}})}}}{8}},}
tg
7
π
30
=
ctg
8
π
30
=
tg
42
∘
=
ctg
48
∘
=
3
(
5
+
1
)
−
2
(
5
+
5
)
2
,
{\displaystyle \operatorname {tg} {\frac {7\,\pi }{30}}=\operatorname {ctg} {\frac {8\,\pi }{30}}=\operatorname {tg} 42^{\circ }=\operatorname {ctg} 48^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2(5+{\sqrt {5}})}}}{2}},}
ctg
7
π
30
=
tg
8
π
30
=
ctg
42
∘
=
tg
48
∘
=
3
(
3
−
5
)
+
2
(
25
−
11
5
)
2
,
{\displaystyle \operatorname {ctg} {\frac {7\,\pi }{30}}=\operatorname {tg} {\frac {8\,\pi }{30}}=\operatorname {ctg} 42^{\circ }=\operatorname {tg} 48^{\circ }={\frac {{\sqrt {3}}(3-{\sqrt {5}})+{\sqrt {2(25-11{\sqrt {5}})}}}{2}},}
tg
π
120
=
ctg
59
π
120
=
tg
1.5
∘
=
ctg
88.5
∘
=
8
−
2
(
2
−
3
)
(
3
−
5
)
−
2
(
2
+
3
)
(
5
+
5
)
8
+
2
(
2
−
3
)
(
3
−
5
)
+
2
(
2
+
3
)
(
5
+
5
)
,
{\displaystyle \operatorname {tg} {\frac {\pi }{120}}=\operatorname {ctg} {\frac {59\,\pi }{120}}=\operatorname {tg} 1.5^{\circ }=\operatorname {ctg} 88.5^{\circ }={\sqrt {\frac {8-{\sqrt {2(2-{\sqrt {3}})(3-{\sqrt {5}})}}-{\sqrt {2(2+{\sqrt {3}})(5+{\sqrt {5}})}}}{8+{\sqrt {2(2-{\sqrt {3}})(3-{\sqrt {5}})}}+{\sqrt {2(2+{\sqrt {3}})(5+{\sqrt {5}})}}}}},}
cos
π
240
=
sin
119
π
240
=
cos
0.75
∘
=
sin
89.25
∘
=
1
16
(
2
−
2
+
2
(
2
(
5
+
5
)
+
3
(
1
−
5
)
)
+
{\displaystyle \cos {\frac {\pi }{240}}=\sin {\frac {119\,\pi }{240}}=\cos 0.75^{\circ }=\sin 89.25^{\circ }={\frac {1}{16}}\left({\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}\left({\sqrt {2(5+{\sqrt {5}})}}+{\sqrt {3}}(1-{\sqrt {5}})\right)+\right.}
+
2
+
2
+
2
(
6
(
5
+
5
)
+
5
−
1
)
)
,
{\displaystyle \left.+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}\left({\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right)\right),}
cos
π
17
=
sin
15
π
34
=
1
8
2
(
2
3
17
−
2
(
85
+
19
17
)
+
17
+
2
(
17
−
17
)
+
17
+
15
)
.
{\displaystyle \cos {\frac {\pi }{17}}=\sin {\frac {15\,\pi }{34}}={\frac {1}{8}}{\sqrt {2\left(2{\sqrt {3{\sqrt {17}}-{\sqrt {2(85+19{\sqrt {17}})}}+17}}+{\sqrt {2(17-{\sqrt {17}})}}+{\sqrt {17}}+15\right)}}.}
sin
π
2
n
+
1
=
1
2
2
−
2
+
⋯
+
2
⏟
n
,
n
∈
N
{\displaystyle \sin {\pi \over 2^{n+1}}={1 \over 2}\underbrace {\sqrt {2-{\sqrt {2+\dots +{\sqrt {2}}}}}} _{n},n\in \mathbb {N} }
cos
π
2
n
+
1
=
1
2
2
+
2
+
⋯
+
2
⏟
n
,
n
∈
N
{\displaystyle \cos {\pi \over 2^{n+1}}={1 \over 2}\underbrace {\sqrt {2+{\sqrt {2+\dots +{\sqrt {2}}}}}} _{n},n\in \mathbb {N} }
sin
π
3
⋅
2
n
=
1
2
2
−
2
+
⋯
+
3
⏟
n
,
n
≥
2
{\displaystyle \sin {\pi \over 3\cdot 2^{n}}={1 \over 2}\underbrace {\sqrt {2-{\sqrt {2+\dots +{\sqrt {3}}}}}} _{n},n\geq 2}
cos
π
3
⋅
2
n
=
1
2
2
+
2
+
⋯
+
3
⏟
n
,
n
≥
2
{\displaystyle \cos {\pi \over 3\cdot 2^{n}}={1 \over 2}\underbrace {\sqrt {2+{\sqrt {2+\dots +{\sqrt {3}}}}}} _{n},n\geq 2}
Синус һәм косинус ярашлы рәүештә берәмек әйләнәлә α мөйөшөнә ярашлы нөктәнең ординатаһы һәм абсциссаһы булғанлыҡтан, берәмек әйләнәнең тигеҙләмәһе йәки Пифагор теоремаһына ярашлы, табабыҙ:
sin
2
α
+
cos
2
α
=
1.
{\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1.}
Был бәйләнеш төп тригонометрик тождество тип атала
Был тигеҙләмәне ярашлы рәүештә косинус һәм синусатың квадратына бүлеп артабан табабыҙ:
1
+
t
g
2
α
=
1
cos
2
α
,
{\displaystyle 1+\mathop {\mathrm {tg} } \,^{2}\alpha ={\frac {1}{\cos ^{2}\alpha }},}
1
+
c
t
g
2
α
=
1
sin
2
α
,
{\displaystyle 1+\mathop {\mathrm {ctg} } \,^{2}\alpha ={\frac {1}{\sin ^{2}\alpha }},}
t
g
α
⋅
c
t
g
α
=
1.
{\displaystyle \mathop {\mathrm {tg} } \,\alpha \cdot \mathop {\mathrm {ctg} } \,\alpha =1.}
Синус һәм косинус — өҙлөкһөҙ функциялар . Тангенс һәм секанстың
±
90
∘
,
±
270
∘
,
±
450
∘
,
…
;
{\displaystyle \pm 90^{\circ },\;\pm 270^{\circ },\;\pm 450^{\circ },\;\dots ;}
0
∘
,
±
180
∘
,
±
360
∘
,
…
.
{\displaystyle 0^{\circ },\;\pm 180^{\circ },\;\pm 360^{\circ },\;\dots .}
өҙөлөү нөктәләре бар.
Косинус һәм секанс — йоп функциялар . Ҡалған дүрт функция — таҡ функциялар , йәғни:
sin
(
−
α
)
=
−
sin
α
,
{\displaystyle \sin \left(-\alpha \right)=-\sin \alpha \,,}
cos
(
−
α
)
=
cos
α
,
{\displaystyle \cos \left(-\alpha \right)=\cos \alpha \,,}
t
g
(
−
α
)
=
−
t
g
α
,
{\displaystyle \mathop {\mathrm {tg} } \,\left(-\alpha \right)=-\mathop {\mathrm {tg} } \,\alpha \,,}
c
t
g
(
−
α
)
=
−
c
t
g
α
,
{\displaystyle \mathop {\mathrm {ctg} } \,\left(-\alpha \right)=-\mathop {\mathrm {ctg} } \,\alpha \,,}
sec
(
−
α
)
=
sec
α
,
{\displaystyle \sec \left(-\alpha \right)=\sec \alpha \,,}
c
o
s
e
c
(
−
α
)
=
−
c
o
s
e
c
α
.
{\displaystyle \mathop {\mathrm {cosec} } \,\left(-\alpha \right)=-\mathop {\mathrm {cosec} } \,\alpha \,.}
y
=
s
i
n
x
,
y
=
c
o
s
x
,
y
=
s
e
c
x
,
y
=
c
o
s
e
c
x
{\displaystyle y=\mathop {\mathrm {sin} } \,x,\quad y=\mathop {\mathrm {cos} } \,x,\quad y=\mathop {\mathrm {sec} } \,x,\quad y=\mathop {\mathrm {cosec} } \,x}
2
π
{\displaystyle 2\pi }
периодлы функциялар ,
y
=
t
g
x
{\displaystyle y=\mathop {\mathrm {tg} } \,x}
y
=
c
t
g
x
{\displaystyle y=\mathop {\mathrm {ctg} } \,x}
π
{\displaystyle \pi }
Килтереү формулалары тип түбәндәге күренештәге формулалар аталалар:
f
(
n
π
+
α
)
=
±
f
(
α
)
,
{\displaystyle f(n\pi +\alpha )=\pm f(\alpha ),}
f
(
n
π
−
α
)
=
±
f
(
α
)
,
{\displaystyle f(n\pi -\alpha )=\pm f(\alpha ),}
f
(
(
2
n
+
1
)
π
2
+
α
)
=
±
g
(
α
)
,
{\displaystyle f\left({\frac {(2n+1)\pi }{2}}+\alpha \right)=\pm g(\alpha ),}
f
(
(
2
n
+
1
)
π
2
−
α
)
=
±
g
(
α
)
.
{\displaystyle f\left({\frac {(2n+1)\pi }{2}}-\alpha \right)=\pm g(\alpha ).}
Бында
f
{\displaystyle f}
g
{\displaystyle g}
n бөтөн һан . Килеп сыҡҡан функция алдына, α ҡыҫынҡы мөйөш тип иҫәпләгәндә, бирелгән координаталар сирегендә тәүге функцияның тамғаһы ниндәй булһа, шул тамғаны ҡуябыҙ, мәҫәлән:
cos
(
π
2
−
α
)
=
sin
α
,
{\displaystyle \cos \left({\frac {\pi }{2}}-\alpha \right)=\sin \alpha \,,}
cos
(
90
∘
−
α
)
=
sin
α
.
{\displaystyle \cos \left(90^{\circ }-\alpha \right)=\sin \alpha \,.}
Ҡайһы бер килтереү формулалары:
α
{\displaystyle \alpha }
π
2
−
α
{\displaystyle {\frac {\pi }{2}}-\alpha }
π
2
+
α
{\displaystyle {\frac {\pi }{2}}+\alpha }
π
−
α
{\displaystyle \pi -\alpha }
π
+
α
{\displaystyle \pi +\alpha }
3
π
2
−
α
{\displaystyle {\frac {3\,\pi }{2}}-\alpha }
3
π
2
+
α
{\displaystyle {\frac {3\,\pi }{2}}+\alpha }
2
π
−
α
{\displaystyle 2\,\pi -\alpha }
sin
α
{\displaystyle \sin \alpha }
cos
α
{\displaystyle \cos \alpha }
cos
α
{\displaystyle \cos \alpha }
sin
α
{\displaystyle \sin \alpha }
−
sin
α
{\displaystyle -\sin \alpha }
−
cos
α
{\displaystyle -\cos \alpha }
−
cos
α
{\displaystyle -\cos \alpha }
−
sin
α
{\displaystyle -\sin \alpha }
cos
α
{\displaystyle \cos \alpha }
sin
α
{\displaystyle \sin \alpha }
−
sin
α
{\displaystyle -\sin \alpha }
−
cos
α
{\displaystyle -\cos \alpha }
−
cos
α
{\displaystyle -\cos \alpha }
−
sin
α
{\displaystyle -\sin \alpha }
sin
α
{\displaystyle \sin \alpha }
cos
α
{\displaystyle \cos \alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
−
ctg
α
{\displaystyle -\operatorname {ctg} \,\alpha }
−
tg
α
{\displaystyle -\operatorname {tg} \,\alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
−
ctg
α
{\displaystyle -\operatorname {ctg} \,\alpha }
−
tg
α
{\displaystyle -\operatorname {tg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
−
tg
α
{\displaystyle -\operatorname {tg} \,\alpha }
−
ctg
α
{\displaystyle -\operatorname {ctg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
−
tg
α
{\displaystyle -\operatorname {tg} \,\alpha }
−
ctg
α
{\displaystyle -\operatorname {ctg} \,\alpha }
Ике мөйөштөң суммаһы һәм айырмаһының тригонометрик функциялары ҡиммәттәре:
sin
(
α
±
β
)
=
sin
α
cos
β
±
cos
α
sin
β
,
{\displaystyle \sin \left(\alpha \pm \beta \right)=\sin \alpha \,\cos \beta \pm \cos \alpha \,\sin \beta ,}
cos
(
α
±
β
)
=
cos
α
cos
β
∓
sin
α
sin
β
,
{\displaystyle \cos \left(\alpha \pm \beta \right)=\cos \alpha \,\cos \beta \mp \sin \alpha \,\sin \beta ,}
tg
(
α
±
β
)
=
tg
α
±
tg
β
1
∓
tg
α
tg
β
,
{\displaystyle \operatorname {tg} \left(\alpha \pm \beta \right)={\frac {\operatorname {tg} \,\alpha \pm \operatorname {tg} \,\beta }{1\mp \operatorname {tg} \,\alpha \,\operatorname {tg} \,\beta }},}
ctg
(
α
±
β
)
=
ctg
α
ctg
β
∓
1
ctg
β
±
ctg
α
.
{\displaystyle \operatorname {ctg} \left(\alpha \pm \beta \right)={\frac {\operatorname {ctg} \,\alpha \,\operatorname {ctg} \,\beta \mp 1}{\operatorname {ctg} \,\beta \pm \operatorname {ctg} \,\alpha }}.}
Өс мөйөштөң суммаһы өсөн оҡшаш формулалар:
sin
(
α
+
β
+
γ
)
=
sin
α
cos
β
cos
γ
+
cos
α
sin
β
cos
γ
+
cos
α
cos
β
sin
γ
−
sin
α
sin
β
sin
γ
,
{\displaystyle \sin \left(\alpha +\beta +\gamma \right)=\sin \alpha \cos \beta \cos \gamma +\cos \alpha \sin \beta \cos \gamma +\cos \alpha \cos \beta \sin \gamma -\sin \alpha \sin \beta \sin \gamma ,}
cos
(
α
+
β
+
γ
)
=
cos
α
cos
β
cos
γ
−
sin
α
sin
β
cos
γ
−
sin
α
cos
β
sin
γ
−
cos
α
sin
β
sin
γ
.
{\displaystyle \cos \left(\alpha +\beta +\gamma \right)=\cos \alpha \cos \beta \cos \gamma -\sin \alpha \sin \beta \cos \gamma -\sin \alpha \cos \beta \sin \gamma -\cos \alpha \sin \beta \sin \gamma .}
Икеләтелгән мөйөш формулалары:
sin
2
α
=
2
sin
α
cos
α
=
2
tg
α
1
+
tg
2
α
=
2
ctg
α
1
+
ctg
2
α
=
2
tg
α
+
ctg
α
,
{\displaystyle \sin 2\alpha =2\sin \alpha \cos \alpha ={\frac {2\,\operatorname {tg} \,\alpha }{1+\operatorname {tg} ^{2}\alpha }}={\frac {2\,\operatorname {ctg} \,\alpha }{1+\operatorname {ctg} ^{2}\alpha }}={\frac {2}{\operatorname {tg} \,\alpha +\operatorname {ctg} \,\alpha }},}
cos
2
α
=
cos
2
α
−
sin
2
α
=
2
cos
2
α
−
1
=
1
−
2
sin
2
α
=
1
−
tg
2
α
1
+
tg
2
α
=
ctg
2
α
−
1
ctg
2
α
+
1
=
ctg
α
−
tg
α
ctg
α
+
tg
α
,
{\displaystyle \cos 2\alpha =\cos ^{2}\alpha \,-\,\sin ^{2}\alpha =2\cos ^{2}\alpha \,-\,1=1\,-\,2\sin ^{2}\alpha ={\frac {1-\operatorname {tg} ^{2}\alpha }{1+\operatorname {tg} ^{2}\alpha }}={\frac {\operatorname {ctg} ^{2}\alpha -1}{\operatorname {ctg} ^{2}\alpha +1}}={\frac {\operatorname {ctg} \,\alpha -\operatorname {tg} \,\alpha }{\operatorname {ctg} \,\alpha +\operatorname {tg} \,\alpha }},}
tg
2
α
=
2
tg
α
1
−
tg
2
α
=
2
ctg
α
ctg
2
α
−
1
=
2
ctg
α
−
tg
α
,
{\displaystyle \operatorname {tg} \,2\alpha ={\frac {2\,\operatorname {tg} \,\alpha }{1-\operatorname {tg} ^{2}\alpha }}={\frac {2\,\operatorname {ctg} \,\alpha }{\operatorname {ctg} ^{2}\alpha -1}}={\frac {2}{\operatorname {ctg} \,\alpha -\operatorname {tg} \,\alpha }},}
ctg
2
α
=
ctg
2
α
−
1
2
ctg
α
=
ctg
α
−
tg
α
2
.
{\displaystyle \operatorname {ctg} \,2\alpha ={\frac {\operatorname {ctg} ^{2}\alpha -1}{2\,\operatorname {ctg} \,\alpha }}={\frac {\operatorname {ctg} \,\alpha -\operatorname {tg} \,\alpha }{2}}.}
Өсләтелгән мөйөш формулалары:
sin
3
α
=
3
sin
α
−
4
sin
3
α
,
{\displaystyle \sin \,3\alpha =3\sin \alpha -4\sin ^{3}\alpha ,}
cos
3
α
=
4
cos
3
α
−
3
cos
α
,
{\displaystyle \cos \,3\alpha =4\cos ^{3}\alpha -3\cos \alpha ,}
tg
3
α
=
3
tg
α
−
tg
3
α
1
−
3
tg
2
α
,
{\displaystyle \operatorname {tg} \,3\alpha ={\frac {3\,\operatorname {tg} \,\alpha -\operatorname {tg} ^{3}\,\alpha }{1-3\,\operatorname {tg} ^{2}\,\alpha }},}
ctg
3
α
=
ctg
3
α
−
3
ctg
α
3
ctg
2
α
−
1
.
{\displaystyle \operatorname {ctg} \,3\alpha ={\frac {\operatorname {ctg} ^{3}\,\alpha -3\,\operatorname {ctg} \,\alpha }{3\,\operatorname {ctg} ^{2}\,\alpha -1}}.}
Тапҡыр мөйөштәр өсөн башҡа формулалар:
sin
4
α
=
cos
α
(
4
sin
α
−
8
sin
3
α
)
,
{\displaystyle \sin \,4\alpha =\cos \alpha \left(4\sin \alpha -8\sin ^{3}\alpha \right),}
cos
4
α
=
8
cos
4
α
−
8
cos
2
α
+
1
,
{\displaystyle \cos \,4\alpha =8\cos ^{4}\alpha -8\cos ^{2}\alpha +1,}
tg
4
α
=
4
tg
α
−
4
tg
3
α
1
−
6
tg
2
α
+
tg
4
α
,
{\displaystyle \operatorname {tg} \,4\alpha ={\frac {4\,\operatorname {tg} \,\alpha -4\,\operatorname {tg} ^{3}\,\alpha }{1-6\,\operatorname {tg} ^{2}\,\alpha +\operatorname {tg} ^{4}\,\alpha }},}
ctg
4
α
=
ctg
4
α
−
6
ctg
2
α
+
1
4
ctg
3
α
−
4
ctg
α
,
{\displaystyle \operatorname {ctg} \,4\alpha ={\frac {\operatorname {ctg} ^{4}\,\alpha -6\,\operatorname {ctg} ^{2}\,\alpha +1}{4\,\operatorname {ctg} ^{3}\,\alpha -4\,\operatorname {ctg} \,\alpha }},}
sin
5
α
=
16
sin
5
α
−
20
sin
3
α
+
5
sin
α
,
{\displaystyle \sin \,5\alpha =16\sin ^{5}\alpha -20\sin ^{3}\alpha +5\sin \alpha ,}
cos
5
α
=
16
cos
5
α
−
20
cos
3
α
+
5
cos
α
,
{\displaystyle \cos \,5\alpha =16\cos ^{5}\alpha -20\cos ^{3}\alpha +5\cos \alpha ,}
tg
5
α
=
tg
α
tg
4
α
−
10
tg
2
α
+
5
5
tg
4
α
−
10
tg
2
α
+
1
,
{\displaystyle \operatorname {tg} \,5\alpha =\operatorname {tg} \alpha {\frac {\operatorname {tg} ^{4}\alpha -10\operatorname {tg} ^{2}\alpha +5}{5\operatorname {tg} ^{4}\alpha -10\operatorname {tg} ^{2}\alpha +1}},}
ctg
5
α
=
ctg
α
ctg
4
α
−
10
ctg
2
α
+
5
5
ctg
4
α
−
10
ctg
2
α
+
1
,
{\displaystyle \operatorname {ctg} \,5\alpha =\operatorname {ctg} \alpha {\frac {\operatorname {ctg} ^{4}\alpha -10\operatorname {ctg} ^{2}\alpha +5}{5\operatorname {ctg} ^{4}\alpha -10\operatorname {ctg} ^{2}\alpha +1}},}
sin
(
n
α
)
=
2
n
−
1
∏
k
=
0
n
−
1
sin
(
α
+
π
k
n
)
{\displaystyle \sin(n\alpha )=2^{n-1}\prod _{k=0}^{n-1}\sin \left(\alpha +{\frac {\pi k}{n}}\right)}
Гамма-функция өсөн Гаусс формулаһынан һәм тултырыу формулаһынан килеп сыға.Муавр формулаһынан тапҡыр мөйөштәр өсөн түбәндәге дөйөм аңлатмаларҙы алырға мөмкин:
sin
(
n
α
)
=
∑
k
=
0
[
(
n
−
1
)
/
2
]
(
−
1
)
k
(
n
2
k
+
1
)
cos
n
−
2
k
−
1
α
sin
2
k
+
1
α
,
{\displaystyle \sin(n\alpha )=\sum _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\cos ^{n-2k-1}\alpha \,\sin ^{2k+1}\alpha ,}
cos
(
n
α
)
=
∑
k
=
0
[
n
/
2
]
(
−
1
)
k
(
n
2
k
)
cos
n
−
2
k
α
sin
2
k
α
,
{\displaystyle \cos(n\alpha )=\sum _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\cos ^{n-2k}\alpha \,\sin ^{2k}\alpha ,}
t
g
(
n
α
)
=
sin
(
n
α
)
cos
(
n
α
)
=
∑
k
=
0
[
(
n
−
1
)
/
2
]
(
−
1
)
k
(
n
2
k
+
1
)
t
g
2
k
+
1
α
∑
k
=
0
[
n
/
2
]
(
−
1
)
k
(
n
2
k
)
t
g
2
k
α
,
{\displaystyle \mathrm {tg} (n\alpha )={\frac {\sin(n\alpha )}{\cos(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {tg} ^{2k+1}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {tg} ^{2k}\alpha }}},}
c
t
g
(
n
α
)
=
cos
(
n
α
)
sin
(
n
α
)
=
∑
k
=
0
[
n
/
2
]
(
−
1
)
k
(
n
2
k
)
c
t
g
n
−
2
k
α
∑
k
=
0
[
(
n
−
1
)
/
2
]
(
−
1
)
k
(
n
2
k
+
1
)
c
t
g
n
−
2
k
−
1
α
,
{\displaystyle \mathrm {ctg} (n\alpha )={\frac {\cos(n\alpha )}{\sin(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {ctg} ^{n-2k}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {ctg} ^{n-2k-1}\alpha }}},}
бында
[
n
]
{\displaystyle [n]}
n
{\displaystyle n}
бөтөн өлөшө ,
(
n
k
)
{\displaystyle {\binom {n}{k}}}
биномиаль коэффициент .
Ярты мөйөш формулалары:
sin
α
2
=
1
−
cos
α
2
,
0
⩽
α
⩽
2
π
,
{\displaystyle \sin {\frac {\alpha }{2}}={\sqrt {\frac {1-\cos \alpha }{2}}},\quad 0\leqslant \alpha \leqslant 2\pi ,}
cos
α
2
=
1
+
cos
α
2
,
−
π
⩽
α
⩽
π
,
{\displaystyle \cos {\frac {\alpha }{2}}={\sqrt {\frac {1+\cos \alpha }{2}}},\quad -\pi \leqslant \alpha \leqslant \pi ,}
tg
α
2
=
1
−
cos
α
sin
α
=
sin
α
1
+
cos
α
,
{\displaystyle \operatorname {tg} \,{\frac {\alpha }{2}}={\frac {1-\cos \alpha }{\sin \alpha }}={\frac {\sin \alpha }{1+\cos \alpha }},}
ctg
α
2
=
sin
α
1
−
cos
α
=
1
+
cos
α
sin
α
,
{\displaystyle \operatorname {ctg} \,{\frac {\alpha }{2}}={\frac {\sin \alpha }{1-\cos \alpha }}={\frac {1+\cos \alpha }{\sin \alpha }},}
tg
α
2
=
1
−
cos
α
1
+
cos
α
,
0
⩽
α
<
π
,
{\displaystyle \operatorname {tg} \,{\frac {\alpha }{2}}={\sqrt {\frac {1-\cos \alpha }{1+\cos \alpha }}},\quad 0\leqslant \alpha <\pi ,}
ctg
α
2
=
1
+
cos
α
1
−
cos
α
,
0
<
α
⩽
π
.
{\displaystyle \operatorname {ctg} \,{\frac {\alpha }{2}}={\sqrt {\frac {1+\cos \alpha }{1-\cos \alpha }}},\quad 0<\alpha \leqslant \pi .}
Ике мөйөш функцияларының ҡабатландығы өсөн формулалар:
sin
α
sin
β
=
cos
(
α
−
β
)
−
cos
(
α
+
β
)
2
,
{\displaystyle \sin \alpha \sin \beta ={\frac {\cos(\alpha -\beta )-\cos(\alpha +\beta )}{2}},}
sin
α
cos
β
=
sin
(
α
−
β
)
+
sin
(
α
+
β
)
2
,
{\displaystyle \sin \alpha \cos \beta ={\frac {\sin(\alpha -\beta )+\sin(\alpha +\beta )}{2}},}
cos
α
cos
β
=
cos
(
α
−
β
)
+
cos
(
α
+
β
)
2
,
{\displaystyle \cos \alpha \cos \beta ={\frac {\cos(\alpha -\beta )+\cos(\alpha +\beta )}{2}},}
tg
α
tg
β
=
cos
(
α
−
β
)
−
cos
(
α
+
β
)
cos
(
α
−
β
)
+
cos
(
α
+
β
)
,
{\displaystyle \operatorname {tg} \,\alpha \,\operatorname {tg} \,\beta ={\frac {\cos(\alpha -\beta )-\cos(\alpha +\beta )}{\cos(\alpha -\beta )+\cos(\alpha +\beta )}},}
tg
α
ctg
β
=
sin
(
α
−
β
)
+
sin
(
α
+
β
)
sin
(
α
+
β
)
−
sin
(
α
−
β
)
,
{\displaystyle \operatorname {tg} \,\alpha \,\operatorname {ctg} \,\beta ={\frac {\sin(\alpha -\beta )+\sin(\alpha +\beta )}{\sin(\alpha +\beta )-\sin(\alpha -\beta )}},}
ctg
α
ctg
β
=
cos
(
α
−
β
)
+
cos
(
α
+
β
)
cos
(
α
−
β
)
−
cos
(
α
+
β
)
.
{\displaystyle \operatorname {ctg} \,\alpha \,\operatorname {ctg} \,\beta ={\frac {\cos(\alpha -\beta )+\cos(\alpha +\beta )}{\cos(\alpha -\beta )-\cos(\alpha +\beta )}}.}
Өс мөйөштөң синустары һәм косинустары ҡабатландыҡтары өсөн оҡшаш формулалар:
sin
α
sin
β
sin
γ
=
sin
(
α
+
β
−
γ
)
+
sin
(
β
+
γ
−
α
)
+
sin
(
α
−
β
+
γ
)
−
sin
(
α
+
β
+
γ
)
4
,
{\displaystyle \sin \alpha \sin \beta \sin \gamma ={\frac {\sin(\alpha +\beta -\gamma )+\sin(\beta +\gamma -\alpha )+\sin(\alpha -\beta +\gamma )-\sin(\alpha +\beta +\gamma )}{4}},}
sin
α
sin
β
cos
γ
=
−
cos
(
α
+
β
−
γ
)
+
cos
(
β
+
γ
−
α
)
+
cos
(
α
−
β
+
γ
)
−
cos
(
α
+
β
+
γ
)
4
,
{\displaystyle \sin \alpha \sin \beta \cos \gamma ={\frac {-\cos(\alpha +\beta -\gamma )+\cos(\beta +\gamma -\alpha )+\cos(\alpha -\beta +\gamma )-\cos(\alpha +\beta +\gamma )}{4}},}
sin
α
cos
β
cos
γ
=
sin
(
α
+
β
−
γ
)
−
sin
(
β
+
γ
−
α
)
+
sin
(
α
−
β
+
γ
)
−
sin
(
α
+
β
+
γ
)
4
,
{\displaystyle \sin \alpha \cos \beta \cos \gamma ={\frac {\sin(\alpha +\beta -\gamma )-\sin(\beta +\gamma -\alpha )+\sin(\alpha -\beta +\gamma )-\sin(\alpha +\beta +\gamma )}{4}},}
cos
α
cos
β
cos
γ
=
cos
(
α
+
β
−
γ
)
+
cos
(
β
+
γ
−
α
)
+
cos
(
α
−
β
+
γ
)
+
cos
(
α
+
β
+
γ
)
4
.
{\displaystyle \cos \alpha \cos \beta \cos \gamma ={\frac {\cos(\alpha +\beta -\gamma )+\cos(\beta +\gamma -\alpha )+\cos(\alpha -\beta +\gamma )+\cos(\alpha +\beta +\gamma )}{4}}.}
Өс мөйөштөң тангенстары һәм котангенстары ҡабатландыҡтары өсөн формулаларҙы, юғарыла килтерелгән ярашлы тигеҙлектәрҙең уң һәм һул яҡтарын бүлеп табырға мөмкин.
sin
2
α
=
1
−
cos
2
α
2
=
tg
2
α
1
+
tg
2
α
{\displaystyle \sin ^{2}\alpha ={\frac {1-\cos 2\,\alpha }{2}}={\frac {\operatorname {tg} ^{2}\,\alpha }{1+\operatorname {tg} ^{2}\,\alpha }}}
tg
2
α
=
1
−
cos
2
α
1
+
cos
2
α
=
sin
2
α
1
−
sin
2
α
,
{\displaystyle \operatorname {tg} ^{2}\,\alpha ={\frac {1-\cos 2\,\alpha }{1+\cos 2\,\alpha }}={\frac {\operatorname {sin} ^{2}\,\alpha }{1-\operatorname {sin} ^{2}\,\alpha }},}
cos
2
α
=
1
+
cos
2
α
2
=
ctg
2
α
1
+
ctg
2
α
,
{\displaystyle \cos ^{2}\alpha ={\frac {1+\cos 2\,\alpha }{2}}={\frac {\operatorname {ctg} ^{2}\,\alpha }{1+\operatorname {ctg} ^{2}\,\alpha }},}
ctg
2
α
=
1
+
cos
2
α
1
−
cos
2
α
,
=
cos
2
α
1
−
cos
2
α
,
{\displaystyle \operatorname {ctg} ^{2}\,\alpha ={\frac {1+\cos 2\,\alpha }{1-\cos 2\,\alpha }},={\frac {\operatorname {cos} ^{2}\,\alpha }{1-\operatorname {cos} ^{2}\,\alpha }},}
sin
3
α
=
3
sin
α
−
sin
3
α
4
,
{\displaystyle \sin ^{3}\alpha ={\frac {3\sin \alpha -\sin 3\,\alpha }{4}},}
tg
3
α
=
3
sin
α
−
sin
3
α
3
cos
α
+
cos
3
α
,
{\displaystyle \operatorname {tg} ^{3}\,\alpha ={\frac {3\sin \alpha -\sin 3\,\alpha }{3\cos \alpha +\cos 3\,\alpha }},}
cos
3
α
=
3
cos
α
+
cos
3
α
4
,
{\displaystyle \cos ^{3}\alpha ={\frac {3\cos \alpha +\cos 3\,\alpha }{4}},}
ctg
3
α
=
3
cos
α
+
cos
3
α
3
sin
α
−
sin
3
α
,
{\displaystyle \operatorname {ctg} ^{3}\,\alpha ={\frac {3\cos \alpha +\cos 3\,\alpha }{3\sin \alpha -\sin 3\,\alpha }},}
sin
4
α
=
cos
4
α
−
4
cos
2
α
+
3
8
,
{\displaystyle \sin ^{4}\alpha ={\frac {\cos 4\alpha -4\cos 2\,\alpha +3}{8}},}
tg
4
α
=
cos
4
α
−
4
cos
2
α
+
3
cos
4
α
+
4
cos
2
α
+
3
,
{\displaystyle \operatorname {tg} ^{4}\,\alpha ={\frac {\cos 4\alpha -4\cos 2\,\alpha +3}{\cos 4\alpha +4\cos 2\,\alpha +3}},}
cos
4
α
=
cos
4
α
+
4
cos
2
α
+
3
8
,
{\displaystyle \cos ^{4}\alpha ={\frac {\cos 4\alpha +4\cos 2\,\alpha +3}{8}},}
ctg
4
α
=
cos
4
α
+
4
cos
2
α
+
3
cos
4
α
−
4
cos
2
α
+
3
.
{\displaystyle \operatorname {ctg} ^{4}\,\alpha ={\frac {\cos 4\alpha +4\cos 2\,\alpha +3}{\cos 4\alpha -4\cos 2\,\alpha +3}}.}
sin
x
−
cos
x
=
2
⋅
sin
(
x
−
π
4
)
{\displaystyle \sin x-\cos x={\sqrt {2}}\cdot \sin \left(x-{\pi \over 4}\right)}
sin
α
±
sin
β
=
2
sin
α
±
β
2
cos
α
∓
β
2
{\displaystyle \sin \alpha \pm \sin \beta =2\sin {\frac {\alpha \pm \beta }{2}}\cos {\frac {\alpha \mp \beta }{2}}}
cos
α
+
cos
β
=
2
cos
α
+
β
2
cos
α
−
β
2
{\displaystyle \cos \alpha +\cos \beta =2\cos {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}}
cos
α
−
cos
β
=
−
2
sin
α
+
β
2
sin
α
−
β
2
{\displaystyle \cos \alpha -\cos \beta =-2\sin {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}}}
tg
α
±
tg
β
=
sin
(
α
±
β
)
cos
α
cos
β
{\displaystyle \operatorname {tg} \alpha \pm \operatorname {tg} \beta ={\frac {\sin(\alpha \pm \beta )}{\cos \alpha \cos \beta }}}
ctg
α
±
ctg
β
=
sin
(
β
±
α
)
sin
α
sin
β
{\displaystyle \operatorname {ctg} \alpha \pm \operatorname {ctg} \beta ={\frac {\sin(\beta \pm \alpha )}{\sin \alpha \sin \beta }}}
1
±
sin
2
α
=
(
sin
α
±
cos
α
)
2
{\displaystyle 1\pm \sin {2\alpha }=(\sin \alpha \pm \cos \alpha )^{2}}
sin
α
±
cos
α
=
2
⋅
sin
(
α
±
π
4
)
.
{\displaystyle \sin \alpha \pm \cos \alpha ={\sqrt {2}}\cdot \sin \left(\alpha \pm {\pi \over 4}\right).}
Ошондай күренеш бар:
A
sin
α
+
B
cos
α
=
A
2
+
B
2
sin
(
α
+
ϕ
)
,
{\displaystyle A\sin \alpha +B\cos \alpha ={\sqrt {A^{2}+B^{2}}}\;\sin(\alpha +\phi ),}
бында
ϕ
{\displaystyle \phi }
sin
ϕ
=
B
A
2
+
B
2
,
cos
ϕ
=
A
A
2
+
B
2
.
{\displaystyle \sin \phi ={\frac {B}{\sqrt {A^{2}+B^{2}}}},\quad \cos \phi ={\frac {A}{\sqrt {A^{2}+B^{2}}}}.}
Бөтә тригонометрик функцияларҙы мөйөш яртыһының тангенсы аша күрһәтеп була.
sin
x
=
sin
x
1
=
2
sin
x
2
cos
x
2
sin
2
x
2
+
cos
2
x
2
=
2
tg
x
2
1
+
tg
2
x
2
{\displaystyle \sin x={\frac {\sin x}{1}}={\frac {2\sin {\frac {x}{2}}\cos {\frac {x}{2}}}{\sin ^{2}{\frac {x}{2}}+\cos ^{2}{\frac {x}{2}}}}={\frac {2\operatorname {tg} {\frac {x}{2}}}{1+\operatorname {tg} ^{2}{\frac {x}{2}}}}}
cos
x
=
cos
x
1
=
cos
2
x
2
−
sin
2
x
2
cos
2
x
2
+
sin
2
x
2
=
1
−
tg
2
x
2
1
+
tg
2
x
2
{\displaystyle \cos x={\frac {\cos x}{1}}={\frac {\cos ^{2}{\frac {x}{2}}-\sin ^{2}{\frac {x}{2}}}{\cos ^{2}{\frac {x}{2}}+\sin ^{2}{\frac {x}{2}}}}={\frac {1-\operatorname {tg} ^{2}{\frac {x}{2}}}{1+\operatorname {tg} ^{2}{\frac {x}{2}}}}}
tg
x
=
sin
x
cos
x
=
2
tg
x
2
1
−
tg
2
x
2
{\displaystyle \operatorname {tg} ~x={\frac {\sin x}{\cos x}}={\frac {2\operatorname {tg} {\frac {x}{2}}}{1-\operatorname {tg} ^{2}{\frac {x}{2}}}}}
ctg
x
=
cos
x
sin
x
=
1
−
tg
2
x
2
2
tg
x
2
{\displaystyle \operatorname {ctg} ~x={\frac {\cos x}{\sin x}}={\frac {1-\operatorname {tg} ^{2}{\frac {x}{2}}}{2\operatorname {tg} {\frac {x}{2}}}}}
sec
x
=
1
cos
x
=
1
+
tg
2
x
2
1
−
tg
2
x
2
{\displaystyle \sec x={\frac {1}{\cos x}}={\frac {1+\operatorname {tg} ^{2}{\frac {x}{2}}}{1-\operatorname {tg} ^{2}{\frac {x}{2}}}}}
cosec
x
=
1
sin
x
=
1
+
tg
2
x
2
2
tg
x
2
{\displaystyle \operatorname {cosec} ~x={\frac {1}{\sin x}}={\frac {1+\operatorname {tg} ^{2}{\frac {x}{2}}}{2\operatorname {tg} {\frac {x}{2}}}}}
Эйлер формулаһы :
e
i
ϑ
=
cos
ϑ
+
i
sin
ϑ
{\displaystyle e^{i\vartheta }=\cos \vartheta +i\sin \vartheta }
комплекслы аргументтың тригонометрик функцияларына экспонента аша (йәки рәттәр ярҙамында) уларҙың ысын аналогтарының аналитик дауамы булараҡ билдәләмә бирергә мөмкинлек бирә:
sin
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
=
e
i
z
−
e
−
i
z
2
i
=
sh
i
z
i
;
{\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}={\frac {e^{iz}-e^{-iz}}{2i}}\,={\frac {\operatorname {sh} iz}{i}};}
cos
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
z
2
n
=
e
i
z
+
e
−
i
z
2
=
ch
i
z
;
{\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}={\frac {e^{iz}+e^{-iz}}{2}}\,=\operatorname {ch} iz;}
tg
z
=
sin
z
cos
z
=
e
i
z
−
e
−
i
z
i
(
e
i
z
+
e
−
i
z
)
;
{\displaystyle \operatorname {tg} \,z={\frac {\sin z}{\cos z}}={\frac {e^{iz}-e^{-iz}}{i(e^{iz}+e^{-iz})}};}
ctg
z
=
cos
z
sin
z
=
i
(
e
i
z
+
e
−
i
z
)
e
i
z
−
e
−
i
z
;
{\displaystyle \operatorname {ctg} \,z={\frac {\cos z}{\sin z}}={\frac {i(e^{iz}+e^{-iz})}{e^{iz}-e^{-iz}}};}
sec
z
=
1
cos
z
=
2
e
i
z
+
e
−
i
z
;
{\displaystyle \sec z={\frac {1}{\cos z}}={\frac {2}{e^{iz}+e^{-iz}}};}
cosec
z
=
1
sin
z
=
2
i
e
i
z
−
e
−
i
z
,
{\displaystyle \operatorname {cosec} \,z={\frac {1}{\sin z}}={\frac {2i}{e^{iz}-e^{-iz}}},}
i
2
=
−
1.
{\displaystyle i^{2}=-1.}
Ярашлы рәүештә, ысын x өсөн,
cos
x
=
Re
(
e
i
x
)
,
{\displaystyle \cos x=\operatorname {Re} (e^{ix}),}
sin
x
=
Im
(
e
i
x
)
.
{\displaystyle \sin x=\operatorname {Im} (e^{ix}).}
Комплекслы синус һәм косинус гиперболик функциялар менән тығыҙ бәйләнгән:
sin
(
x
+
i
y
)
=
sin
x
ch
y
+
i
cos
x
sh
y
,
{\displaystyle \sin(x+iy)=\sin x\,\operatorname {ch} \,y+i\cos x\,\operatorname {sh} \,y,}
cos
(
x
+
i
y
)
=
cos
x
ch
y
−
i
sin
x
sh
y
.
{\displaystyle \cos(x+iy)=\cos x\,\operatorname {ch} \,y-i\sin x\,\operatorname {sh} \,y.}
Юғарыла һынап кителгән тригонометрик функциялар үҙсәнлектәренең күпселеге комплекслы осраҡта ла һаҡланалар. Ҡайһы бер өҫтәлмә үҙсәнлектәр:
комплекслы синус һәм косинус, ысын аргументлыларҙан айырмалы рәүештә, модуле буйынса теләһә ниндәй ҙур ҡиммәттәр ҡабул итә алалар;
комплекслы синус һәм косинустың бөтә нулдәре ысын күсәрҙә яталар. Түбәндәге графиктарҙа комплекслы яҫылыҡ һүрәтләнгән, ә функцияларҙың ҡиммәттәре төҫ менән айырып күрһәтелгән. Асыҡлыҡ абсолют ҡиммәтте сағылдыра (ҡара — ноль). Төҫ аргументтан һәм мөйөштән картаға ярашлы үҙгәрә.
Комплекслы яҫылыҡта тригонометрик функциялар
sin
z
{\displaystyle \sin \,z}
cos
z
{\displaystyle \cos \,z}
tg
z
{\displaystyle \operatorname {tg} \,z}
ctg
z
{\displaystyle \operatorname {ctg} \,z}
sec
z
{\displaystyle \sec \,z}
cosec
z
{\displaystyle \operatorname {cosec} \,z}
Синус һыҙығы (2-се һүрәттә AB һыҙығы) һинд математиктарында башта «арха-джива» («ярым ян», йәғни бирелгән дуға хордаһының яртыһы, сөнки дуға менән хорда керешле янды хәтерләтә) тип аталған. Аҙаҡ «арха» һүҙе алып ташлана һәм синус һыҙығын «джива» тип кенә атай башлайҙар. Ғәрәп математиктары, һинд китаптарын санскриттан тәржемәләп, «джива» һүҙен ғәрәптәрҙең кереш һәм хорданы аңлатҡан «ватар» һүҙенә тәржемәләмәгәндәр, ә уны ғәрәп хәрефтәре менән транскрипциялайҙар һәм синус һыҙығын «джиба» (جيب ) тип атайҙар. Ғәрәп телендә ҡыҫҡа һуҙынҡылар тамғаланмайҙар, ә «джиба» һүҙендә оҙон «и» ярымһуҙынҡы «й» кеүек тамғалана, ғәрәптәр синус һыҙығының атамаһын «джайб» тип әйтә башлайҙар, ул һүҙмә-һүҙ «соҡор», «ҡыуышлыҡ» тигәнде аңлата. Ғәрәп яҙмаларын Европа тәржемәселәре латин теленә тәржемәләгәндә, «джайб» һүҙен латин телендә шул уҡ мәғәнәне аңлатҡан sinus — «синус» һүҙенә әйләндерәләр. «Косинус» термины (лат. cosinus лат. complementi sinus өҫтәлмә синус.
Хәҙерге
sin
,
cos
{\displaystyle \sin ,~\cos }
Б. Кавальери һәм Уильям Отред тарафынан индерелгән һәм Леонард Эйлер хеҙмәттәрендә нығытылған.
«Тангенс» (лат. tangens «секанс» (лат. secans Томас Финке тарафынан уның «Геометрия круглого» (Geometria rotundi, 1583) китабында индерелгән.
Тригонометрик функциялар тигән термин үҙе Клюгель тарафынан 1770 йылда индерелгән.
Һуңғараҡ инде кире тригонометрик функциялар өсөн дә терминдар индерелә — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — Жозеф Луи Лагранж һ.б. тарафынан (лат. arcus «арк» приставкаһын өҫтәп яһалғандар.
Бермант А. Ф. Люстерник Л. А . Тригонометрия. — М.: Наука, 1967.Тригонометрик функциялар Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М .: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.Выгодский М. Я. Справочник по элементарной математике . — М .: Наука, 1978.Двайт Г. Б. Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М .: Наука, 1973. — С. 70—102.Кожеуров П. А . Тригонометрия. — М.: Физматгиз, 1963.Маркушевич А. И . Замечательные синусы. — М.: Наука, 1974.Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: «Советская Энциклопедия», 1984. — Т. 5. — с. 436 .Тригонометрические функции // Энциклопедический словарь юного математика / Ред. коллегия, Гнеденко Б. В . (гл. ред.), Савин А. П . и др. — М.: Педагогика, 1985 (1989). — С. 299—301—305. — 352 с., ил. ISBN 5-7155-0218-7 (стр. 342 2018 йыл 7 февраль архивланған . 343 2018 йыл 7 февраль архивланған .
Тригонометрические функции // Справочник по математике (для ср. уч. заведений) / Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 240—258. — 480 с. {иҫкәрмәләр}}
↑ Большая советская энциклопедия 1 издание т. 27 "Знак математический" М.1933г.
↑ Справочник по элементарной математике, 1978 , с. 282—284↑ Справочник по элементарной математике, 1978 , с. 271—272↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. 1. — Москва: Наука, 1998. — ISBN 5-02-015231-5 .↑ В формулах, содержащих логарифм в правой части равенств, константы интегрирования
C
{\displaystyle \scriptstyle C}




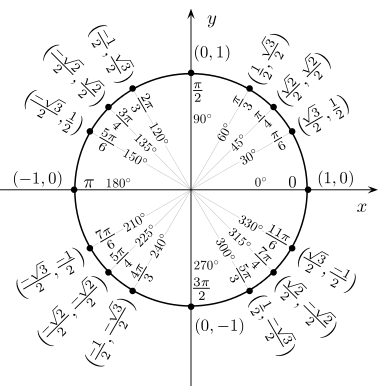


































































































































































































































































![{\displaystyle \sin(n\alpha )=\sum _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\cos ^{n-2k-1}\alpha \,\sin ^{2k+1}\alpha ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb020e5dfc3b2d5dfe1d1a0c571487ce387a8153)
![{\displaystyle \cos(n\alpha )=\sum _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\cos ^{n-2k}\alpha \,\sin ^{2k}\alpha ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84f285d7cb530e87d8a9e33cff84fd4a4c9a8205)
![{\displaystyle \mathrm {tg} (n\alpha )={\frac {\sin(n\alpha )}{\cos(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {tg} ^{2k+1}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {tg} ^{2k}\alpha }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8800a20a70495802fc2de287bb98d155e14720b1)
![{\displaystyle \mathrm {ctg} (n\alpha )={\frac {\cos(n\alpha )}{\sin(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {ctg} ^{n-2k}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {ctg} ^{n-2k-1}\alpha }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90744f04ee2a1e34b1f0763e310c1c1d071f240d)
![{\displaystyle [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)


































































