Эйлер формулаһы

Геометрический смысл формулы Эйлера

Эйлер формулаһы комплекслы экспонентаны тригонометрик функциялар менән бәйләй. Уны индергән Леонард Эйлер хөрмәтенә аталған.

Эйлер формулаһы теләһә ниндәй комплекслы (айырым алғанда ысын) $x$ һаны өсөн түбәндәге тигеҙлек үтәлә тип раҫлай:

$e^{ix}=\cos x+i\sin x$,

бында $e$ — артабанғы формула менән бирелгән математик константаларҙың иң мөһимдәренең береһе: $e=\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}$,

$i$ — уйланма берәмек.

Тарихы

Эйлер формулаһы беренсе тапҡыр инглиз математигы Роджер Котстың (Ньютондың ярҙамсыһы) «Философские труды Королевского общества» журналында 1714 йылда баҫылып сыҡҡан «Логометрия» (лат. Logometria) мәҡәләһендә килтерелә һәм 1722 йылда баҫылып сыҡҡан «Гармония мер» (лат. Harmonia mensurarum) китабында, автор вафат булғандан һуң, яңынан баҫтырыла. Котс уны күп геометрик төҙөүҙәр араһында ҙур булмаған һөйләм рәүешендә килтерә, уны хәҙерге математика теленә күсергәндән һәм тамғалағы хатаһын төҙәткәндән һуң формула ошондай күренештә була:

$\ln(\cos x+i\sin x)=ix$.

Эйлер формуланы уның ғәҙәттәге күренешендә 1740 йылдағы мәҡәләһендә һәм «Введение в анализ бесконечно малых» (лат. Introductio in analysin infinitorum) (1748) китабында баҫтыра, иҫбатлауҙы формуланың уң һәм һул яҡтарының дәрәжәле рәттәргә сикһеҙ тарҡалмаларының тигеҙлегенә таянып төҙөй. Эйлер ҙа, Котс та формуланың геометрик интерпретацияларын күҙ алдына килтерә алмайҙар: комплекслы һандар тураһында комплекслы яҫылыҡтағы нөктәләр кеүек ҡараш сама менән 50 йыл үткәс К. Весселдә барлыҡҡа килә.

Сығарылма формулалар

Эйлер формулаһы ярҙамында $\sin$ һәм $\cos$ функцияларына түбәндәгесә билдәләмә бирергә мөмкин:

$\sin x={\frac {e^{ix}-e^{-ix}}{2i}}$,

$\cos x={\frac {e^{ix}+e^{-ix}}{2}}$.

Артабан комплекслы үҙгәреүсәнле тригонометрик функциялар төшөнсәһе индерергә мөмкин. $x=iy$ булһын, ул саҡта:

$\sin iy={\frac {e^{-y}-e^{y}}{2i}}=i\mathop {\mathrm {sh} } \,y$,

$\cos iy={\frac {e^{-y}+e^{y}}{2}}=\mathop {\mathrm {ch} } \,y$.

Биш фундаменталь математик константаларҙы бәйләүсе билдәле Эйлер тождествоһы:

$e^{i\pi }+1=0$

Эйлер формулаһының $x=\pi$ булғандағы айырым осрағы булып тора.

Һандар теорияһында ҡулланылышы

Һандарҙың аналитик теорияһында йыш ҡына $\sum \limits _{x\in X}{e^{2\pi if(x)}}$ күренешендәге махсус суммалар ҡарала, бында $X$ — ниндәйҙер ҡаралған объекттар күмәклеге, ә $f:\ X\to {\mathbb {R} }$ — объекттарҙың өйрәнелгән үҙсәнлектәрен сағылдырыусы функция.

Бөтөн һандарҙы өйрәнгән һандар теорияһы өсөн беренсе нәүбәттә, ирекле $n$ бөтөн һанына ҡағылған, Эйлер формулаһынан сығарылған индикаторлы тождестволар әһәмиәткә эйә.

$\sum \limits _{k=1}^{p}{e^{2\pi {\frac {nk}{p}}i}}=p[p|n]=\left\{{\begin{matrix}p,&n\equiv 0{\pmod {p}}\\0,&n\not \equiv 0{\pmod {p}}\end{matrix}}\right.$

$\int \limits _{0}^{1}{e^{2\pi n\alpha i}}=[n=0]=\left\{{\begin{matrix}1,&n=0\\0,&n\not =0\end{matrix}}\right.$

Комплекслы анализда ҡулланылышы

Эйлер формулаһы арҡаһында комплекслы һандың тригонометрик һәм күрһәткесле тип аталған яҙыуы барлыҡҡа килә: $x=a+ib=|x|(\cos \varphi +i\sin \varphi )=|x|e^{i\varphi }$.

Шулай уҡ әһәмиәтле эҙемтәһе тип комплекслы һанды ирекле дәрәжәгә күтәреү формулаларын һанарға мөмкин: $x=|x|e^{i\varphi }$, $x^{n}=|x|^{n}e^{ni\varphi }$. Был формуланың геометрик мәғәнәһе ошолай: $x$ һанын $n$-сы дәрәжәгә күтәргәндә уның үҙәккә тиклем алыҫлығы $n$-сы дәрәжәгә күтәрелә, ә $OX$ күсәренә ҡарата боролош мөйөшө $n$ тапҡыр ҙурая.

Дәрәжәгә күтәреү формулаһы бөтөн $n$ һандары өсөн генә түгел, ысын һандар өсөн дә дөрөҫ. Атап әйткәндә, һандың күрһәткесле яҙыуы теләһә ниндәй комплекслы һандан тамыр табырға мөмкинлек бирә.

Тригонометрия менән үҙ-ара бәйләнеш

Эйлер формулаһы математик анализ һәм тригонометрия араһында бәйләнеш бирә, шулай уҡ синус һәм косинус функцияларын экспоненциаль функцияның үлсәнгән суммалары итеп интерпретацияларға мөмкинлек бирә:

$\cos x=\mathrm {Re} \{e^{ix}\}={e^{ix}+e^{-ix} \over 2}$

$\sin x=\mathrm {Im} \{e^{ix}\}={e^{ix}-e^{-ix} \over 2i}.$

Юғарыла килтерелгән тигеҙләмәләрҙе Эйлер формулаларын ҡушыу һәм алыу юлы менән:

$e^{ix}=\cos x+i\sin x\;$

$e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x\;$

һәм артабан синусҡа йәки косинусҡа ҡарата сығарып алып була.

Шулай уҡ был формулалар комплекслы үҙгәреүсәнле тригонометрик функцияларҙың билдәләмәһе булып хеҙмәт итә алалар. Мәҫәлән, x = iy алмаштырып ҡуйыуын башҡарып, табабыҙ:

$\cos(iy)={e^{-y}+e^{y} \over 2}=\cosh(y)$

$\sin(iy)={e^{-y}-e^{y} \over 2i}=-{1 \over i}{e^{y}-e^{-y} \over 2}=i\sinh(y).$

Комплекслы экспоненталар тригонометрик иҫәпләүҙәрҙе ябайлаштырырға мөмкинлек бирәләр, сөнки улар менән, синусоидаль компоненталар менән эш иткәнгә ҡарағанда, манипуляция яһау ябайыраҡ. Ҡараштарҙың береһе синусоидаларҙы ярашлы экспоненциаль аңлатмаларға үҙгәртеүҙе күҙ уңында тота. Ябайлаштырғандан һуң аңлатманың һөҙөмтәһе ысын һан булып ҡала. Мәҫәлән:

${\begin{aligned}\cos x\cdot \cos y&={\frac {(e^{ix}+e^{-ix})}{2}}\cdot {\frac {(e^{iy}+e^{-iy})}{2}}\\&={\frac {1}{2}}\cdot {\frac {e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2}}\\&={\frac {1}{2}}\left[\underbrace {\frac {e^{i(x+y)}+e^{-i(x+y)}}{2}} _{\cos(x+y)}+\underbrace {\frac {e^{i(x-y)}+e^{-i(x-y)}}{2}} _{\cos(x-y)}\right].\end{aligned}}$

Икенсе ҡараштың асылы синусоидаларҙы комплекслы аңлатманың ысын өлөшө сифатында күрһәтеүҙән һәм туранан-тура комплекслы аңлатма менән манипуляциялар яһауҙан тора. Мәҫәлән:

${\begin{aligned}\cos(nx)&=\mathrm {Re} \{\ e^{inx}\ \}=\mathrm {Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \}\\&=\mathrm {Re} \{\ e^{i(n-1)x}\cdot (e^{ix}+e^{-ix}-e^{-ix})\ \}\\&=\mathrm {Re} \{\ e^{i(n-1)x}\cdot \underbrace {(e^{ix}+e^{-ix})} _{2\cos(x)}-e^{i(n-2)x}\ \}\\&=\cos[(n-1)x]\cdot 2\cos(x)-\cos[(n-2)x].\end{aligned}}$

Был формула n-дың бөтөн ҡиммәттәре һәм x-тың (радиандарҙа) ирекле ҡиммәттәре өсөн cos(nx) ҡиммәттәрен рекурсив иҫәпләү өсөн ҡулланыла.

Иҫбатлау

Эйлер формулаһын Маклорен рәтен файҙаланып иҫбатларға мөмкин. $e^{ix}$ функцияһын a = 0 нөктәһенең тирә-яғында $x$-тың дәрәжәләре буйынса Тейлор рәтенә (Маклорен рәтенә) тарҡатабыҙ. Табабыҙ:

$e^{ix}=1+{\frac {ix}{1!}}+{\frac {(ix)^{2}}{2!}}+{\frac {(ix)^{3}}{3!}}+\ldots =\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\ldots \right)+i\left({\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\ldots \right)$

Ләкин

$1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\ldots =\cos x$

${\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\ldots =\sin x$

Шуға күрә $e^{ix}=\cos x+i\sin x$, ш. и. и. һ..

Күргәҙмә демонстрация

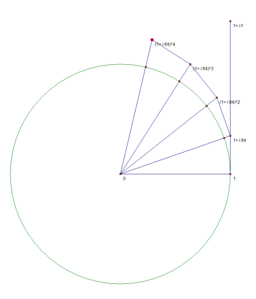
Билдәле булыуынса, $e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}$. Түбәндә килтерелгән һүрәттәр $e^{i\varphi }=\lim _{n\to \infty }\left(1+{\frac {i\varphi }{n}}\right)^{n}$ сикләнмәһе берәмек әйләнәлә ятҡан нөктәгә ынтылыуын иллюстрациялай, һәм был нөктәнән 1 нөктәһенә тиклем дуғаның оҙонлоғо $\varphi$-ға тигеҙ. Был, атап әйткәндә, $\lim \limits _{x\to 0}{\frac {\sin x}{x}}=1$ булыуы менән бәйле.

• 
  n=1
• 
  n=2
• 
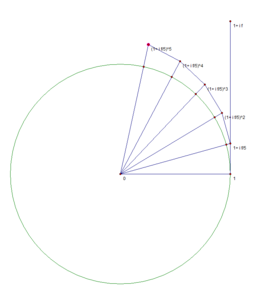
  n=3
• 
  n=4
• 
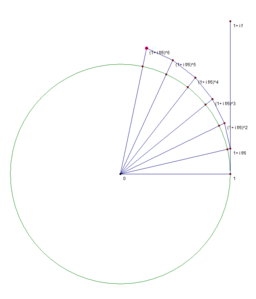
  n=5
• 
  n=6
• 
  n=8
• 
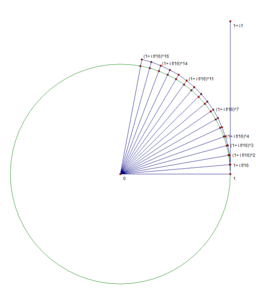
  n=16

$\varphi$ үҙгәргәндә $e^{\varphi i}$-тың үҙгәреү процессын шулай уҡ сығарылма аша асыҡ күрһәтергә мөмкин. $\left({e^{x}}\right)'=e^{x}$ һәм $\left({e^{f(x)}}\right)'=f'(x)e^{f(x)}$ булыуы билдәле. Шул уҡ факт функцияның комплекслы ҡиммәте өсөн дә дөрөҫ булып ҡала. $f(\varphi )=e^{\varphi i}$ функцияһын ҡарап, $f'(\varphi )=if(\varphi )$ булыуын табабыҙ. Комплекслы һандарҙың геометрик күрһәтелешендә $i$-гә ҡабатлау 90 градусҡа боролошҡа тиң булғанлыҡтан, $f(\varphi )=e^{\varphi i}$ функцияһының һәм уның сығарылмаһының график һүрәтләнеше, физик мәғәнәһе билдәле булған үҙәккә ынтылышлы көстөң тәьҫире һыҙмаһына оҡшаш була.

Комплекслы һандың күрһәткесле формаһы

Комплекслы һандарҙың күрһәткесле һәм тригонометрик формалары үҙ-ара Эйлер формулаһы менән бәйләнгәндәр.

$z$ комплекслы һаны тригонометрик формала $z=r(\cos \varphi +i\sin \varphi )$ күренешендә булһын, ти. Эйлер формулаһы нигеҙендә йәйә эсендәге аңлатманы күрһәткесле аңлатмаға алмаштырырға мөмкин. Нәтижәлә табабыҙ:

$z=re^{i\varphi }$

Был яҙыу комплекслы һандың күрһәткесле формаһы тип атала. Шулай уҡ, тригонометрик формалағы кеүек, бында $r=|z|$ , $\varphi =\arg z$.

Шулай уҡ ҡарағыҙ

• Муавр формулаһы
• Леонард Эйлер хөрмәтенә аталған объекттар теҙеме

Әҙәбиәт

• Гутов А. З. Аналог формулы Эйлера для обобщённых синуса и косинуса // Современные методы физико-математических наук. Труды международной конференции. Орёл, 2006. С. 35—37. 2020 йыл 25 сентябрь архивланған.
• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
• Стиллвелл Д. Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — 530 с.