Эллипс

Эллипсис менән бутамаҫҡа.

Эллипс, уның фокустары һәм төп күсәрҙәре

Эллипс конус киҫелеше булараҡ, уның Данделен шарҙары ярҙамында геометрик юл менән табылған фокустары һәм директрисалары.

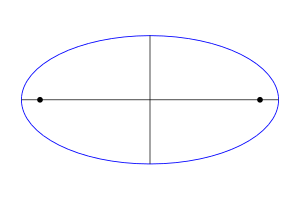
Э́ллипс (бор. грек. ἔλλειψις «опущение; нехватка һүҙҙәренән, <эксцентриситеты 1>-гә етмәгән») — яҫылыҡ һәм түңәрәк цилиндрҙың киҫелеше булған йәки әйләнәнең яҫылыҡҡа ортогональ проекцияһы булараҡ төҙөп булған яҫылыҡтағы йомоҡ кәкре һыҙыҡ.

Әйләнә эллипстың айырым осрағы булып тора. Гипербола һәм парабола менән бер рәттән, эллипс конус киҫелеше һәм квадрика булып тора.

Билдәләмә

Эллипс — Евклид яҫылығының, ике бирелгән $F_{1}$ һәм $F_{2}$ (фокустар тип аталған) нөктәләренән алыҫлыҡтарының суммаһы даими һәм фокустар араһындағы алыҫлыҡтан ҙурыраҡ булған нөктәләрҙең геометрик урыны M, йәғни

$|F_{1}M|+|F_{2}M|=2\cdot a,$ шуның менән бергә $|F_{1}F_{2}|<2\cdot a.$

Комментарийҙар

• Эллипсҡа шулай уҡ
  • әйләнәнән, аффиналы үҙгәртеү ҡулланып алып булған фигура тип билдәләмә бирергә мөмкин.
  • әйләнәнең яҫылыҡҡа ортогональ проекцияһы тип билдәләмә бирергә мөмкин.
  • Яҫылыҡ һәм түңәрәк цилиндрҙың киҫелеше тип билдәләмә бирергә мөмкин.

Бәйле билдәләмәләр

• Эллипстың фокустары аша үткән, остары эллипста ятҡан AB киҫеге бирелгән эллипстың ҙур күсәре тип атала. Ҙур күсәрҙең оҙонлоғо 2a-ға тигеҙ.
• Эллипстың ҙур күсәренә перпендикуляр булған һәм ҙур күсәрҙең үҙәк нөктәһе аша үткән, остары эллипста ятҡан CD киҫеге эллипстың бәләкәй күсәре тип атала.
• Эллипстың ҙур һәм бәләкәй күсәрҙәренең киҫешеү нөктәһе уның үҙәге тип атала.
• Эллипстың үҙәгенән ҙур һәм бәләкәй күсәрҙәренең түбәләренә үткәрелгән киҫектәр ярашлы рәүештә эллипстың ҙур ярымкүсәре һәм бәләкәй ярымкүсәре тип аталалар, һәм a һәм b тип тамғаланалар.
• Һәр фокустан эллипстағы бирелгән нөктәгә тиклемге $r_{1}$ һәм $r_{2}$ алыҫлыҡтары был нөктәләге фокаль радиустар тип аталалар.
• $c={\frac {|F_{1}F_{2}|}{2}}$ алыҫлығы фокаль алыҫлыҡ тип атала.
• $e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$ дәүмәле эксцентриситет тип атала .
• Эллипстың диаметры тип уның үҙәге аша үтеүсе ирекле хорданы атайҙар. Эллипстың бәйле диаметрҙары тип уның, беренсе диаметрға параллель хордаларҙың урталары икенсе диаметрҙа ятҡан диаметрҙар парын атайҙар. Был осраҡта икенсе диаметрға параллель хордаларҙың урталары беренсе диаметрҙа ята.
• Эллипстың бирелгән нөктәләге радиусы тип эллипстың үҙәген был нөктә менән тоташтырыусы киҫек, шулай уҡ уның оҙонлоғо атала. Ул артабанғы формула буйынса иҫәпләнә $r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}$, бында $\varphi$ — радиус һәм ҙур ярымкүсәр араһындағы мөйөш.
• Фокаль параметр $p={\frac {b^{2}}{a}}$ тип фокус аша үтеүсе һәм эллипстың ҙур күсәренә перпендикуляр булған хорда оҙонлоғоноң яртыһы атала.
• Бәләкәй һәм ҙур ярымкүсәрҙәр оҙонлоҡтарының сағыштырмаһы эллипстың ҡыҫылыу коэффициенты йәки эллипслылыҡ тип атала: $k={\frac {b}{a}}.$ $(1-k)={\frac {a-b}{a}},$ тигеҙ булған дәүмәл эллипсты ҡыҫыу тип атала. Әйләнә өсөн ҡыҫылыу коэффициенты берәмеккә тигеҙ, ҡыҫыу — нулгә. Эллипстың ҡыҫылыу коэффициенты һәм эксцентриситеты соотношением $k^{2}=1-e^{2}.$ нисбәте менән бәйләнгән.
• Һәр фокус өсөн директриса тип аталған шундай тура һыҙыҡ бар, такая, что отношение расстояния от произвольной точки эллипстың теләһә ниндәй нөктәһенән уның фокусына тиклемге алыҫлыҡтың был нөктәнән бирелгән тура һыҙыҡҡа тиклемге алыҫлыҡҡа сағыштырмаһы эллипстың эксцентриситетына тигеҙ. Бөтә эллипс был тура һыҙыҡтан фокус ятҡан яҡта ята. Эллипстың директрисаһы тигеҙләмәһе ярашлы рәүештә $\left(\mp {\frac {p}{1+e}},\,0\right)$ фокустары өсөн каноник күренештә ошолай яҙыла $x=\pm {\frac {p}{e\left(1+e\right)}}$. Фокус һәм директриса араһындағы алыҫлыҡ ${\frac {p}{e}}$ тигеҙ.

Эллипстың элементтары араһында нисбәттәр

Эллипстың өлөштәре («Бәйле билдәләмәләр» бүлегендәге тасуирламаны ҡарағыҙ)

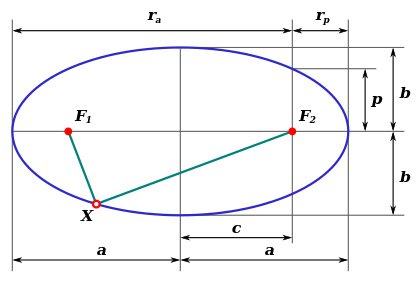
• ${\boldsymbol {a}}$ — ҙур ярымкүсәр;
• ${\boldsymbol {b}}$ — бәләкәй ярымкүсәр;
• ${\boldsymbol {c}}$ — фокаль алыҫлыҡ (фокустар араһындағы ярымалыҫлыҡ);
• ${\boldsymbol {p}}$ — фокаль параметр;
• ${\boldsymbol {r}}_{p}$ — перифокус алыҫлығы (фокустан эллипстағы нөктәгә тиклемге иң бәләкәй алыҫлыҡ);
• ${\boldsymbol {r}}_{a}$ — апофокус алыҫлығы (фокустан эллипстағы нөктәгә тиклемге иң ҙур алыҫлыҡ);

$a^{2}=b^{2}+c^{2}$

$e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1).$.

$p={\frac {b^{2}}{a}}$

	${\boldsymbol {a}}$	${\boldsymbol {b}}$	${\boldsymbol {c}}$	${\boldsymbol {p}}$	${\boldsymbol {r_{p}}}$	${\boldsymbol {r_{a}}}$
${\boldsymbol {a}}$ — ҙур ярымкүсәр	${\boldsymbol {a}}$	$a={\frac {b}{\sqrt {1-e^{2}}}}$	$a={\frac {c}{e}}$	$a={\frac {p}{1-e^{2}}}$	$a={\frac {r_{p}}{1-e}}$	$a={\frac {r_{a}}{1+e}}$
${\boldsymbol {b}}$ — бәләкәй ярымкүсәр	$b=a{\sqrt {1-e^{2}}}$	${\boldsymbol {b}}$	$b={\frac {c~{\sqrt {1-e^{2}}}}{e}}$	$b={\frac {p}{\sqrt {1-e^{2}}}}$	$b=r_{p}{\sqrt {\frac {1+e}{1-e}}}$	$b=r_{a}{\sqrt {\frac {1-e}{1+e}}}$
${\boldsymbol {c}}$ — фокаль алыҫлыҡ	$c=ae$	$c={\frac {be}{\sqrt {1-e^{2}}}}$	${\boldsymbol {c}}$	$c={\frac {pe}{1-e^{2}}}$	$c={\frac {r_{p}e}{1-e}}$	$c={\frac {r_{a}e}{1+e}}$
${\boldsymbol {p}}$ — фокаль параметр	$p=a(1-e^{2})$	$p=b~{\sqrt {1-e^{2}}}$	$p=c~{\frac {1-e^{2}}{e}}$	${\boldsymbol {p}}$	$p=r_{p}(1+e)$	$p=r_{a}(1-e)$
${\boldsymbol {r}}_{p}$ — перифокус алыҫлығы	$r_{p}=a(1-e)$	$r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}$	$r_{p}=c~{\frac {1-e}{e}}$	$r_{p}={\frac {p}{1+e}}$	${\boldsymbol {r}}_{p}$	$r_{p}=r_{a}{\frac {1-e}{1+e}}$
${\boldsymbol {r}}_{a}$ — апофокус алыҫлығы	$r_{a}=a(1+e)$	$r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}$	$r_{a}=c~{\frac {1+e}{e}}$	$r_{a}={\frac {p}{1-e}}$	$r_{a}=r_{p}~{\frac {1+e}{1-e}}$	${\boldsymbol {r}}_{a}$

Координаталарҙа күрһәтеү

Эллипс икенсе тәртиптәге кәкре һыҙыҡ булараҡ

Эллипс үҙәк икенсе тәртиптәге кәкре һыҙыҡ булып тора һәм түбәндәге күренештәге дөйөм тигеҙләмәне ҡәнәғәтләндерә

$a_{11}x^{2}+a_{22}y^{2}+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0,$

$D>0$ һәм $\Delta I<0$ инварианттарында, бында:

$\Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{12}&a_{22}&a_{23}\\a_{13}&a_{23}&a_{33}\end{vmatrix}},$

$D={\begin{vmatrix}a_{11}&a_{12}\\a_{12}&a_{22}\end{vmatrix}}=a_{11}a_{22}-a_{12}^{2},$

$I=tr{\begin{pmatrix}a_{11}&a_{12}\\a_{12}&a_{22}\end{pmatrix}}=a_{11}+a_{22}.$

Икенсе тәртиптәге кәкре һыҙыҡ инварианттары һәм эллипстың ярымкүсәрҙәре араһындағы нисбәт (эллипстың үҙәге координаталар башы менән тап килгән һәм $a_{33}=-1$ булған осраҡта ғына дөрөҫ):

$\Delta =-{\frac {1}{a^{2}}}{\frac {1}{b^{2}}},$

$D={\frac {1}{a^{2}}}{\frac {1}{b^{2}}},$

$I={\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}.$

Нисбәттәр  

Әгәр дөйөм тигеҙләмәне

$AX^{2}+BXY+CY^{2}+DX+EY+F=0$ күренешендә күсереп яҙһаҡ,

ул саҡта эллипс үҙәгенең координаталары:

$h={\frac {BE-2CD}{4AC-B^{2}}},k={\frac {BD-2AE}{4AC-B^{2}}},$

әйләнеү мөйөшө түбәндәге аңлатманан табыла

$tg(2\Theta )={\frac {B}{A-C}}.$

Күсәр векторҙары йүнәлештәре:

${\begin{pmatrix}B&(C-A+{\sqrt {(C-A)^{2}+B^{2}}})\end{pmatrix}},{\begin{pmatrix}B&(C-A-{\sqrt {(C-A)^{2}+B^{2}}})\end{pmatrix}}$

бынан сығып

$tg(\Theta )={\frac {C-A\pm {\sqrt {(C-A)^{2}+B^{2}}}}{B}}$

Ярымкүсәрҙәр оҙонлоғо түбәндәге аңлатмалар менән бирелә

$a={\sqrt {\frac {2F'({\sqrt {(A-C)^{2}+B^{2}}}+A+C)}{4AC-B^{2}}}}$

$b={\sqrt {\frac {2F'}{{\sqrt {(A-C)^{2}+B^{2}}}+A+C}}}$

Кире нисбәт - дөйөм тигеҙләмәнең коэффициенттарын эллипс параметрҙарынан - каноник тигеҙләмәгә (түбәндәге бүдекте ҡарағыҙ) координаталар системаһы өсөн Θ мөйөшөнә боролош һәм $(x_{c},y_{c})$ нөктәһенә күсереү аңлатмаларын ҡуйып табып була:

${\frac {x'^{2}}{a^{2}}}+{\frac {y'^{2}}{b^{2}}}=1$

$x'=(x-x_{c})cos\Theta +(y-y_{c})sin\Theta$

$y'=-(x-x_{c})sin\Theta +(y-y_{c})cos\Theta$

Урынына ҡуйыуҙы башҡарып һәм йәйәләрҙе асып дөйөм тигеҙләмәнең коэффициенттары өсөн артабанғы аңлатмаларҙы табабыҙ:

$A=a^{2}(sin\Theta )^{2}+b^{2}(cos\Theta )^{2}$

$B=2(b^{2}-a^{2})sin\Theta cos\Theta$

$C=a^{2}(cos\Theta )^{2}+b^{2}(sin\Theta )^{2}$

$D=-2Ax_{c}-By_{c}$

$E=-Bx_{c}-2Cy_{c}$

$F=Ax_{c}^{2}+Cy_{c}^{2}+Bx_{c}y_{c}-a^{2}b^{2}$

Әгәр мөйөштө генә индереп, эллипстың үҙәген координаталар башында ҡалдырһаҡ, ул саҡта

$D=0$

$E=0$

$F=-a^{2}b^{2}$

Эллипстың Декарт координаталар системаһында бирелгән дөйөм күренештәге тигеҙләмәлә $A,B,C,D,E,F$ коэффициенттары (йәки, шул уҡ, $a_{11},2a_{12},a_{22},2a_{13},2a_{23},a_{33}$) ирекле даими ҡабатлашыусыға тиклем аныҡлыҡ менән билдәлеләр, йәғни юғарыла килтерелгән яҙыу һәм

$AkX^{2}+BkXY+CkY^{2}+DkX+EkY+Fk=0$

бында $k\neq 0$, эквивалентлылар.

$1/a^{2}+1/b^{2}=Ak+Ck$ аңлатмаһы теләһә ниндәй $k$ өсөн үтәләсәк тип көтөргә ярамай.

Инварианта $I$ һәм ярымкүсәрҙәр араһындағы нисбәт дөйөм күренештә түбәндәгесә:

${\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {A+C}{F\cdot (A\cdot h^{2}+B\cdot h\cdot k+C\cdot k^{2}-1)}}={\frac {I}{F'}}$

где $F'=F\cdot (A\cdot h^{2}+B\cdot h\cdot k+C\cdot k^{2}-1)$     - коэффициент $F$ при переносе начала координат в центр эллипса, когда уравнение приводится к виду

$AX^{2}+BXY+CY^{2}+F'=0$

Другие инварианты находятся в следующих соотношениях:

$-{\frac {\Delta }{F'^{3}}}={\frac {D}{F'^{2}}}={\frac {1}{a^{2}}}{\frac {1}{b^{2}}}$

Каноник тигеҙләмә

Теләһә ниндәй эллипс өсөн шундай Декарт координаталар системаһын табып була, унда эллипс түбәндәге тигеҙләмә менән бирелә:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$

Был тигеҙләмә эллипстың канониик тигеҙләмәһе тип атала. Ул үҙәге координаталар башында, күсәрҙәре координаталар күсәрҙәре менән тап килгән эллипстың тигеҙләмәһе.

Нисбәттәр  

Асыҡлыҡ өсөн $0<b\leqslant a$ тип уйлайыҡ. Был осраҡта $a$ һәм $b$ дәүмәлдәре — ярашлы рәүештә, эллипстың ҙур һәм бәләкәй ярымкүсәрҙәре.

Эллипстың ярымкүсәрҙәрен белгән хәлдә уның фокаль алыҫлығын һәм эксцентриситетын табырға була:

$\left|F_{1}F_{2}\right|=2{\sqrt {a^{2}-b^{2}}},\;\;\;e={\frac {\sqrt {a^{2}-b^{2}}}{a}}<1.$

Эллипстың фокустарының координаталары:

$\left(ae,\,0\right),\;\;\;\left(-ae,\,0\right).$

Эллипстың ике директрисаһы бар, уларҙың тигеҙләмәләрен ошолай яҙып була

$x={\frac {a}{e}},\;\;\;x=-{\frac {a}{e}}.$

Фокаль параметр (йәғни фокус аша үткән һәм эллипстың күсәренә перпендикуляр булған хорда оҙонлоғоноң яртыһы) тигеҙ

$p={\frac {b^{2}}{a}}.$

Фокаль радиустар, йәғни фокустарҙан кәкре һыҙыҡтың теләһә ниндәй нөктәһенә тиклемге алыҫлыҡ $\left(x,\,y\right):$

$r_{1}=a+ex,\;\;\;r_{2}=a-ex.$

Мөйөшсә коэффициенты $k:$ булған хордаларға бәйле диаметрҙың тигеҙләмәһе:

$y=-{\frac {b^{2}}{a^{2}k}}x.$

Эллипсҡа $(x_{0},y_{0})$ нөктәһендә үткәрелгән тейеүсе тигеҙләмәһе түбәндәге күренештә $:$

${\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}=1.$

$y=mx+k$ тура һыҙығының ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ эллипсҡа тейеү шарты түбәндәге бәйлелек рәүешендә яҙыла $:$ $k^{2}=m^{2}a^{2}+b^{2}$

$\left(x_{1},y_{1}\right):$ нөктәһе аша үтеүсе тейеүселәрҙең тигеҙләмәһе

${\frac {y-y_{1}}{x-x_{1}}}={\frac {-x_{1}y_{1}\pm {\sqrt {b^{2}x_{1}^{2}+a^{2}y_{1}^{2}-a^{2}b^{2}}}}{a^{2}-x_{1}^{2}}}$

Мөйөшсә коэффициенты $k$-ға тигеҙ булған тейеүселәрҙең тигеҙләмәһе:

$y=kx\pm {\sqrt {k^{2}a^{2}+b^{2}}};$

бындай тура һыҙыҡтың эллипсҡа тейеү нөктәһе (йәки шул уҡ, эллипсҡа тейеүсе тангенсы $k$) булған мөйөш яһаған нөктәләре:

$x=\mp {\frac {ka^{2}}{\sqrt {k^{2}a^{2}+b^{2}}}},y=\pm {\frac {b^{2}}{\sqrt {k^{2}a^{2}+b^{2}}}}.$

$\left(x_{1},y_{1}\right):$ нөктәһендә нормалдең тигеҙләмәһе

${\frac {y-y_{1}}{x-x_{1}}}={\frac {a^{2}y_{1}}{b^{2}x_{1}}}.$

Параметрлы формала тигеҙләмәләр

Эллипсты параметрлауҙы геометрик иллюстрациялау (анимация).

Эллипстың каноник тигеҙләмәһе параметрланырға мөмкин:

${\begin{cases}x=a\,\cos t\\y=b\,\sin t\end{cases}}\;\;\;0\leqslant t\leqslant 2\pi ,$

бында $t$ — параметр.

Тик әйләнә осрағында ғына (йәғни $a=b$ булғанда) $t$ параметры абсциссалар күсәренең ыңғай йүнәлеше һәм бирелгән нөктәнең радиус-векторы араһындағы мөйөш була.

Поляр координаталарҙа

Әгәр эллипстың фокусын полюс, ә ҙур күсәрҙе — поляр күсәр итһәң, ул саҡта уның поляр координаталарҙа $\left(\rho ,\varphi \right)$ тигеҙләмәһе ошондай күренештә була

$\rho ={\frac {p}{1\pm e\cos \varphi }},$

бында e — эксцентриситет, ә p — фокаль параметр. Минус тамғаһы поляр координаталар полюсының һул фокуста, ә плюс тамғаһы — уң фокуста урынлашҡан осраҡҡа ярашлы.

Сығарыу  

r₁ һәм r₂ — беренсе һәм икенсе фокустарҙан эллипстағы бирелгән нөктәгә тиклемге алыҫлыҡтар булһын, ти. Шулай уҡ координаталар системаһының полюсы беренсе фокуста, ә $\varphi$ мөйөшө икенсе фокусҡа йүнәлештән иҫәпләнә, ти. Ул саҡта, эллипстың билдәләмәһенән,

$r_{1}+r_{2}=2a.$

Ошонан сығып,

$r_{2}^{2}=\left(2a-r_{1}\right)^{2}=4a^{2}-4ar_{1}+r_{1}^{2}.$

Икенсе яҡтан, косинустар теоремаһынан

$r_{2}^{2}=r_{1}^{2}+4c^{2}-4r_{1}c\cos \varphi .$

Һуңғы ике тигеҙләмәнән $r_{2}$ алып ташлап, табабыҙ

$r_{1}={\frac {a^{2}-c^{2}}{a-c\cos \varphi }}.$

$p=a(1-e^{2})$ булыуын иҫәпкә алып,

эҙләнгән тигеҙләмәне табабыҙ.

Әгәр эллипстың үҙәген полюс, ә ҙур күсәрҙе — поляр күсәр итһәк, ул саҡта уның тигеҙләмәһе поляр координаталарҙа $\left(\rho ,\varphi \right)$ ошондай күренештә булыр

$\rho ={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}={\frac {ab}{\sqrt {a^{2}\sin ^{2}\varphi +b^{2}\cos ^{2}\varphi }}}.$

Эллипстың дуғаһының оҙонлоғо (s) уның (θ) параметрына бәйле

Эллипс дуғаһы оҙонлоғо

Яҫы һыҙыҡтың дуғаһы оҙонлоғо түбәндәге формула буйынса иҫәпләнә:

$l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\,dt.$

Эллипстың параметрлы бирелеше менән файҙаланып түбәндәге аңлатманы табабыҙ:

$l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,dt.$

$b^{2}=a^{2}\left(1-e^{2}\right)$ алмаштырып ҡуйыуынан һуң дуға оҙонлоғо өсөн аңлатма һуңғы күренеште ала:

$l=a\int \limits _{t_{1}}^{t_{2}}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt,\;\;\;e<1.$

Килеп сыҡҡан интеграл эллиптик интегралдар ғаиләһенә ҡарай, уларҙы элементар функциялар аша күрһәтеп булмай, һәм икенсе төрҙәге эллиптик интегралға ҡайтып ҡала $E\left(t,e\right)$. Айырым алғанда, эллипстың периметры тигеҙ:

$l=4a\int \limits _{0}^{\pi /2}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt=4aE(e)$,

бында $E\left(e\right)$ — 2-се төрҙәге тулы эллиптик интеграл.

Периметр өсөн яҡынса формулалар

$L\approx 4{\frac {\pi ab+(a-b)^{2}}{a+b}}.$

Эллипстың эксцентриситеты ~0,988 булғанда был формуланың иң ҙур хатаһы ~0,63 % (күсәрҙәр нисбәте ~1/6,5). Хата һәр саҡ ыңғай.

Түбәндәге формула эксцентриситеттарҙың киң диапазонында яҡынса ике тапҡыр бәләкәй хата бирә:

$L\approx 4\cdot \left(a^{x}+b^{x}\right)^{\left(1/x\right)}$, где $x={\frac {\ln 2}{\ln {\frac {\pi }{2}}}}.$

Эллипстың эксцентриситеты ~0,980 булғанда был формуланың иң ҙур хатаһы ~0,36 % (күсәрҙәр нисбәте ~1/5). Хата шулай уҡ һәр саҡ ыңғай.

Рамануджан формулаһы $0,05<a/b<20$ булғанда һиҙелерлек яҡшыраҡ теүәллек бирә:

$L\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right].$

Эллипстың эксцентриситеты ~0,980 (күсәрҙәр нисбәте ~1/5) булғанда хата ~0,02 % тәшкил итә. Хата һәр саҡ тиҫкәре.

Рамануджандың икенсе формулаһы тағы ла теүәлерәк:

$L\approx \pi (a+b)\left[1+{\frac {3\left({\frac {a-b}{a+b}}\right)^{2}}{10+{\sqrt {4-3\left({\frac {a-b}{a+b}}\right)^{2}}}}}\right]$

Периметр өсөн теүәл формулалар

Джеймс Айвори һәм Фридрих Бессель бер-береһенә бәйһеҙ рәүештә эллипстың периметры өсөн формула табалар:

$L=\pi (a+b)\left[1+\sum \limits _{n=1}^{\infty }\left[{\frac {(2n-1)!!}{(2n-1)\cdot 2^{n}\cdot n!}}\left({\frac {a-b}{a+b}}\right)^{n}\right]^{2}\right]$

Альтернатив формула

$L={\frac {2\pi aN(1-e^{2})}{M({\sqrt {1-e^{2}}})}},$

бында $M(x)$ — 1 һәм $x$-тың арифметик-геометрик уртаһы, ә $N(x)$ — 1 һәм $x$-тың модификацияланған арифметик-геометрик уртаһы, ул С. Ф. Адлай тарафынан 2012 йылдағы мәҡәләлә индерелә.

Эллипстың һәм уның сегментының майҙаны

Эллипстың майҙаны түбәндәге формула буйынса иҫәпләнә

$S=\pi ab.$

Һулға ҡабарынҡы дуға һәм $\left(x,\,y\right)$ һәм $\left(x,\,-y\right):$ нөктәләре аша үткән хорда араһындағы сегменттың майҙаны

$S={\frac {\pi ab}{2}}-{\frac {b}{a}}\left(x\,{\sqrt {a^{2}-x^{2}}}+a^{2}\arcsin {\frac {x}{a}}\right).$

Әгәр эллипс $Ax^{2}+Bxy+Cy^{2}=1$ тигеҙләмәһе менән бирелһә, ул саҡта майҙанды түбәндәге формула буйынса табырға була

$S={\frac {2\pi }{\sqrt {4AC-B^{2}}}}$.

Эллипсты төҙөү

Эллипсограф в действии

Эллипсты энә, еп һәм ҡәләм ярҙамында төҙөү.

Основная статья — статья «Построение эллипса» в Викиучебнике.

Эллипсты төҙөү өсөн инструменттар булып торалар:

• эллипсограф;
• эллипстың фокустарына ҡаҙалған һәм 2a оҙонлоғондағы еп менән бәйләнгән ике энә, уны ҡәләм менән тартып ҡуялар.

Циркуль йәки циркуль һәм линейка ярҙамында эллипста ятҡан теләһә ниндәй һанда нөктәләр төҙөргә мөмкин, ләкин бөтә эллипсты тулыһынса түгел.

Өсмөйөш менән бәйле эллипстар

• Брокар эллипсы — фокустары Брокар нөктәләрендә булған эллипс
• Мандарт эллипсы
• Штейнер эллипсы

Башҡа үҙсәнлектәре

• Оптик
  • Фокустарҙың береһендә урынлашҡан сығанаҡтан таралған яҡтылыҡ эллипстан, сағылған нурҙар икенсе фокуста киҫешерлек итеп сағыла.
  • Теләһә ҡайһы фокустан ситтә урынлашҡан сығанаҡтан таралған яҡтылыҡ эллипстан, сағылған нурҙар бер фокуста ла киҫешмәҫлек итеп сағыла.
• Әгәр $F_{1}$ һәм $F_{2}$ — эллипстың фокустары булһа, ул саҡта эллипста ятҡан теләһә ниндәй X нөктәһе өсөн, был нөктәләге тейеүсе һәм $(F_{1}X)$ тура һыҙығы араһындағы мөйөш был тура һыҙыҡ менән $(F_{2}X)$ тура һыҙығы араһындағы мөйөшкә тигеҙ.
• Эллипсты киҫеүсе ике параллель тура һыҙыҡ менән киҫеп алынған киҫектәрҙең урталары аша үткән тура һыҙыҡ һәр саҡ эллипстың үҙәге аша үтә. Был циркуль һәм линейка ярҙамында төҙөп эллипстың үҙәген еңел генә табырға мөмкинлек бирә, ә артабан күсәрен, түбәһен һәм фокустарын.
• Эллипстың вертикаль күсәре буйлап һуҙылған астроидаһы эволютаһы була.
• Эллипстың күсәрҙәре менән киҫешеү нөктәләре уның түбәләре була.
• Эллипстың Эксцентриситеты, йәғни $e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1),$ сағыштырмаһы эллипстың һуҙынҡылығын характерлай. Эксцентриситет нулгә яҡыныраҡ булған һайын, эллипс күберәк әйләнәне хәтерләтә һәм киреһенсә, эксцентриситет берәмеккә ни тиклем яҡын булһа, ул шул тиклем нығыраҡ һуҙынҡы.
  • Әгәр эллипстың эксцентриситеты нулгә тигеҙ булһа (шул уҡ, фокаль алыҫлыҡ нулгә тигеҙ кеүек: $F_{1}F_{2}=0$), ул саҡта эллипс әйләнәгә әүерелә.
• Экстремаль үҙсәнлектәре
  • Әгәр $F$ — ҡабарынҡы фигура һәм $T_{n}$ — $F$-ҡа ҡамалған иң ҙур майҙанлы $n$-мөйөш булһа, ул саҡта

    $S(T_{n})\geq S(F)\cdot {\frac {n}{\sin(2\cdot \pi /n)}}{2\cdot \pi },$

бында $S(F)$ $F$ фигураһының майҙанын аңлата.

• Улай ғына түгел, тигеҙлек үтәлә шул саҡта һәм тик шул саҡта ғына, әгәр $F$ эллипс менән сикләнһә.

• Бирелгән майҙанды сикләүсе бөтә ҡабарынҡы йомоҡ кәкре һыҙыҡтар араһында эллипс иң ҙур аффина оҙонлоғона эйә.

• Әгәр ирекле эллипс ABC өсмөйөшөнә ҡамалған һәм P һәм Q фокустары булһа, ул саҡта уның өсөн түбәндәге нисбәт дөрөҫ

${\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.$

• Әгәр баҫҡысты (тура һыҙыҡтың сикһеҙ нәҙек киҫеге) горизонталь иҙәндә вертикаль стенаға һөйәһәң, һәм баҫҡыстың бер осо стена буйлап шыуһа (һәр ваҡыт уға тейеп), ә икенсе осо иҙән буйлап шыуһа (һәр ваҡыт уға тейеп), ул саҡта баҫҡыстың теләһә ниндәй билдәләнгән нөктәһе (уның осонда түгел) ниндәйҙер эллипс дуғаһы буйлап хәрәкәт итәсәк. Был үҙсәнлек, нөктәне баҫҡыс-киҫек эсендә түгел, ә уның уйланылған дауамында алғанда дөрөҫ була. Был үҙсәнлек юғарыла тасуирланған^[⇨] эллипсографта ҡулланыла.

• Эллипста ятҡан $(x_{0},y_{0})$ нөктәһе аша үткән тейеүсенең тигеҙләмәһе:

${\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}=1.$

Шулай уҡ ҡарағыҙ

• Икенсе тәртиптәге кәкре һыҙыҡ
• Парабола
• Каустика
• Эллипсоид
• Эллипсограф
• Ике нөктә араһындағы алыҫлыҡтарҙың айырмаһы даими булған кәкре һыҙыҡ — гипербола,
• даими бәйләнештәге — Аполлоний түңәрәге,
• даими ҡабатландыҡлы — Кассини овалы.

Әҙәбиәт

• Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70—73.
• Селиванов Д. Ф. Эллипс // Брокгауз һәм Ефрондың энциклопедик һүҙлеге: 86 томда (82 т. һәм 4 өҫтәмә том). — СПб., 1890—1907. (рус.)
• А. В. Акопян, А. А. Заславский. Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
• И. Бронштейн. Эллипс // Квант, № 9, 1970.
• А. И. Маркушевич. Замечательные кривые // «Популярные лекции по математике», выпуск 4.

Һылтанмалар

• S.Sykora, Approximations of Ellipse Perimeters and of the Complete Elliptic Integral E(x). Review of known formulae
• Grard P. Michon. Perimeter of an Ellipse (Final Answers) 2011 йыл 27 октябрь архивланған., 2000—2005. — 20 c.
• Видео: Как нарисовать эллипс