Вектор (геометрия)
| Вектор | |
 | |

Геометрияла вектор — тура һыҙыҡтың йүнәлешле киҫеге, йәғни ҡайһы осо башы, ә ҡайһыһы — аҙағы икәне күрһәтелгән киҫек атала[1].
Башы нөктәһендә һәм осо нөктәһендә булған векторҙы тип тамғалау ҡабул ителгән. Векторҙар шулай уҡ өҫтөнә уҡ (ҡайһы берҙә — һыҙыҡ) ҡуйылған бәләкәй латин хәрефтәре менән дә тамғаланалар, мәҫәлән . Икенсе таралған яҙыу ысулы: вектор символын ҡалын шрифт менән билдәләү: .
Геометрияла вектор тәбиғи рәүештә күсереүгә (параллель күсереү) тиңләштерелә, был вектор атамаһының (лат. vector, алып барыусы, илтеүсе) килеп сығыуына асыҡлыҡ индерә. Ысынлап та, һәр йүнәлешле киҫек яҫылыҡта йәки арауыҡта ниндәйҙер параллель күсереүҙе бер мәғәнәле билдәләй: әйтәйек, векторы нөктәһен нөктәһенә күсереүсе күсереүҙе тәбиғи рәүештә билдәләй , шулай уҡ киреһе, нөктәһен нөктәһенә күсереүсе параллель күсереү, берҙән-бер йүнәлешле киҫеген билдәләй (берҙән-бер — әгәр бер үк йүнәлештәге һәм оҙонлоҡтағы бөтә йүнәлешле киҫектәрҙе тигеҙ тип иҫәпләгәндә — йәғни уларҙы ирекле векторҙар тип ҡарағанда; ысынлап та, параллель күсереүҙә бөтә нөктәләр ҙә бер үк йүнәлештә бер үк алыҫлыҡҡа күсәләр, шулай аңлағанда ).
Векторға күсереү тип интерпретация биреү, векторҙарҙы ҡушыу ғәмәлен тәбиғи рәүештә һәм интуитив күренеп торған ысул менән — ике (йәки бер нисә) күсереүҙең композицияһы (эҙмә-эҙ ҡулланыу) булараҡ, индерергә мөмкинлек бирә; шул уҡ векторҙы һанға ҡабатлау ғәмәленә лә ҡағыла.
Төп төшөнсәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]Вектор тип береһе башы, ә икенсеһе осо тип аталған ике нөктә буйынса төҙөлгән йүнәлешле киҫек атала.
Векторҙың координаталары уның осо менән башындағы нөктәләрҙең координаталары айырмаһы булараҡ билдәләнә. Мәҫәлән, координаталар яҫылығында, әгәр башы менән осоноң координаталары бирелһә: һәм , ул саҡта векторҙың координаталары: була.
векторының оҙонлоғо тип ике һәм нөктәләре араһындағы алыҫлыҡ атала, уны ғәҙәттә тип тамғалайҙар.
Векторҙар араһында нуль ролен нуль вектор уйнай, уның башы менән осо тап килә ; уның, башҡа векторҙарҙан айырмалы рәүештә, йүнәлеше юҡ [2].

Векторҙарҙы координаталар аша биреү өсөн векторҙың күсәргә проекцияһы (йүнәлешле тура һыҙыҡҡа, һүрәтте ҡарағыҙ) төшөнсәһе ҙур роль уйнай. Проекция тип векторҙың башы һәм осоноң бирелгән тура һыҙыҡҡа проекциялары менән төҙөлгән киҫектең оҙонлоғо атала, шуның менән бергә, әгәр проекцияның йүнәлеше күсәрҙең йүнәлеше менән тап килһә, проекцияға плюс тамғаһы бирелә, башҡа осраҡта — минус тамғаһы. Проекция бирелгән векторҙың оҙонлоғоноң, бирелгән вектор менән күсәр араһындағы мөйөш косинусына ҡабатландығына тигеҙ; векторҙың уға перпендикуляр күсәргә проекцияһы нулгә тигеҙ.
Ҡулланылышы
[үҙгәртергә | сығанаҡты үҙгәртеү]Векторҙа геометрияла һәм ғәмәли фәндәрҙә киң ҡулланыу таба, унда йүнәлеше булған дәүмәлдәрҙе (көс, тиҙлек һ. б.) һүрәтләү өсөн ҡулланылалар. Векторҙарҙы ҡулланыу күп ғәмәлдәрҙе ябайлаштыра — мәҫәлән, тура һыҙыҡтар һәм киҫектәр араһындағы мөйөштө табыу, фигураларҙың майҙанын иҫәпләү. Компьютерлы графикала вектор-нормалдәр есемде дөрөҫ яҡтыртыу булдырыу өсөн ҡулланыла. Векторҙарҙы ҡулланыу координаталар ысулы нигеҙенә һалынырға мөмкин.
Векторҙарҙың төрҙәре
[үҙгәртергә | сығанаҡты үҙгәртеү]Ҡайһы берҙә, векторҙар сифатында бөтә йүнәлешле киҫектәр күмәклеген ҡарайһы урынға, (башы һәм осо тап килмәгән бөтә йүнәлешле киҫектәрҙе төрлө векторҙар тип ҡарап), был күмәклектең ниндәйҙер модификацияһын (факторкүмәклек) ғына алалар, йәғни, ҡайһы бер йүнәлешле киҫектәрҙе, әгәр уларҙың оҙонлоҡтары тигеҙ һәм йүнәлештәре тап килһә, уларҙың баштары һәм остары төрлө булһа ла, тигеҙ векторҙар тип ҡарайҙар; шулай итеп, һәр векторға, оҙонлоҡтары һәм йүнәлештәре бер төрлө булған, ләкин башланғыс нөктәһе (һәм осо) төрлө булған бөтә йүнәлешле киҫектәр класы тап килә.
Шулай, «ирекле», «шыумалы» һәм «беркетелгән» векторҙар була. Был төрҙәр ике векторҙың тигеҙлеге төшөнсәһе менән генә айырылалар.
- Ирекле векторҙар тураһында һөйләгәндә, бер үк оҙонлоҡтағы һәм йүнәлешле векторҙарҙы тиң һанайҙар;
- шыумалы векторҙар тураһында һөйләгәндә — добавляют, шыумалы тигеҙ векторҙарҙың баштары тап килергә йәки был векторҙарҙы һүрәтләүсе йүнәлешле киҫектәр ятҡан бер тура һыҙыҡта ятырға тейештәр тип өҫтәйҙәр (береһен икенсеһе менән үҙҙәре билдәләгән йүнәлештә күсереп тап килтерергә мөмкин);
- беркетелгән векторҙар тураһында һөйләгәндә — йүнәлештәре лә, башланғыс нөктәләре лә тап килгән векторҙар ғына тигеҙ тип иҫәпләнәләр (йәғни был осраҡта факторизация юҡ: тигеҙ тип һанарға мөмкин булған төрлө башланғыс нөктәле ике беркетелгән вектор юҡ).
Формаль рәүештә:
Әгәр һәм дүртмөйөштәре — параллелограммдар булырлыҡ һәм нөктәләре табылһа, һәм ирекле векторҙары тигеҙ тип атала.
Әгәр:
- нөктәләре бер тура һыҙыҡта ятһалар,
- һәм векторҙары ирекле векторҙар булараҡ үҙ-ара тигеҙ булһалар,
һәм шыумалы векторҙары тигеҙ тип аталалар. Шыумалы векторҙар бигерәк тә механикала ҡулланылалар. Шыумалы векторҙың механикала иң ябай миҫалы — ҡаты есемгә тәьҫир итеүсе көс. Көс векторының башын ул ятҡан тура һыҙыҡ буйлап күсереү, теләһә ниндәй нөктәгә ҡарата көс моментын үҙгәртмәй; хатта векторҙың дәүмәлен һәм йүнәлешен үҙгәртмәйсә, уны икенсе тура һыҙыҡҡа күсереү, уның моментын үҙгәртергә мөмкин (хатта һәр ваҡыт тиерлек үҙгәртә): шуға күрә моментты иҫәпләгәндә көстө ирекле вектор итеп ҡарарға ярамай, йәғни, уны ҡаты есемдең теләһә ниндәй нөктәһенә һалынған тип иҫәпләргә ярамай.
Әгәр һәм , һәм нөктәләре пар-пар тап килһә, һәм беркетелгән векторҙарытигеҙ тип атала.
Бер осраҡта вектор тип йүнәлешле киҫек атала, ә башҡа осраҡтарҙа төрлө векторҙар — төрлө йүнәлешле киҫектәрҙең ниндәйҙер конкрет эквивалентлылыҡ бәйләнеше менән билдәләнеүсе эквивалентлылыҡ кластары. Шуның менән бергә, векторҙың төрөн билдәләүсе («ирекле», «беркетелгән» һ. б. ш.) эквивалентлылыҡ бәйләнеше төрлөсә булырға мөмкин. Ябайыраҡ әйткәндә, внутри класса эквивалентлылыҡ класы эсендә уға ингән бөтә йүнәлешле киҫектәр тигеҙ тип ҡарала, һәм һәр вектор бөтә класты кәүҙәләндерергә мөмкин.
Векторҙар өҫтөндә бөтә ғәмәлдәр (ҡушыу, һанға ҡабатлау, скаляр һәм векторлы ҡабатлау, модулен йәки оҙонлоғон, векторҙар араһындағы мөйөштө иҫәпләү һ. б.) бөтә төрҙәге векторҙар өсөн нигеҙҙә бер төрлө билдәләнә, төрҙәрҙәге айырмалыҡ был осраҡта, башланғыс нөктәләре төрлө булған шыумалы һәм беркетелгән ике вектор араһында ғәмәлдәрҙе башҡарауға сикләү ҡуйылыуына ғына ҡайтып ҡала (шулай, беркетелгән ике вектор өсөн, әгәр башланғыс нөктәләре төрлө булһа, ҡушыу ғәмәле тыйыла — йәки мәғәнәһе юҡ ; әммә был ғәмәл рөхсәт ителгән бөтә осраҡтарҙа — йәки мәғәнәһе булһа — ул ирекле векторҙар өсөн булған кеүек үк). Шуға күрә йыш ҡына векторҙың төрө күрһәтелмәй, ул контекстан аңлашылып тора тип иҫәпләнә. Улай ғына түгел, бер үк вектор мәсьәләнең контексына бәйле, шыумалы, беркетелгән һәм ирекле вектор тип ҡаралырға мөмкин, мәҫәлән, механикала есемгә ҡуйылған көс векторҙары, тиң көслө векторҙы тапҡанда, ҡуйылған нөктәһенә бәйһеҙ рәүештә ҡушылырға мөмкиндәр (статикала ла, динамикала ла масса үҙәге хәрәкәтен, импульс үҙгәреүен тикшергәндә һ. б.), әммә әйләнеү моментын иҫәпләгәндә (шулай уҡ статикала һәм динамикала), ҡуйылыу нөктәһен иҫәпкә алмайынса бер-береһенә ҡушыу башҡарыла алмай.
Векторҙар араһында бәйләнеш
[үҙгәртергә | сығанаҡты үҙгәртеү]Ике вектор, әгәр улар параллель тура һыҙыҡтарҙа йәки бер тура һыҙыҡта ятһалар, коллинеар тип аталалар. Ике вектор, әгәр улар коллинеар һәм бер яҡҡа йүнәлгән булһалар, бер йүнәлешле векторҙар тип аталалар; әгәр улар коллинеар һәм төрлө яҡҡа йүнәлгән булһалар, ҡапма-ҡаршы йүнәлешле векторҙар тип аталалар. Икенсе билдәләмә лә бар: ике нулдән айырмалы һәм векторҙары, әгәр тигеҙлеге үтәлерлек шундай һаны булһа, коллинеар векторҙар тип аталалар[3]
Өс вектор, әгәр уларҙы уртаҡ башланғыс нөктәгә һалғанда бер яҫылыҡта ятһалар, компланар векторҙар тип аталалар[3].
Координаталар аша күрһәтеү
[үҙгәртергә | сығанаҡты үҙгәртеү]
Векторҙар менән эш иткәндә. йыш ҡына ниндәйҙер декарт координаталар системаһын индерәләр һәм унда, векторҙы базис векторҙар буйынса тарҡатып, уның координаталарын билдәләйҙәр. Базис буйынса тарҡатыуҙы геометрик, векторҙың координаталар күсәрҙәренә проекциялары ярҙамында күҙ алдына килтерергә мөмкин. Әгәр векторҙың башының һәм осоноң координаталары билдәле булһа, векторҙың үҙенең координаталарын векторҙың осоноң координаталарынан уның башының координаталарын алып табалар.
Базис итеп йыш ҡына, күсәрҙәренә ярашлы рәүештә тип тамғаланған координаталар орттарын һайлайҙар. Ул саҡта векторын
- тип яҙырға мөмкин
Теләһә ниндәй геометрик үҙсәнлеген координаталарҙа яҙырға мөмкин, ошонан һуң геометрик тикшеренеү алгебраик тикшеренеүгә әйләнә һәм йыш ҡына ябайлаша. Киреһе, дөйөм әйткәндә, бик үк дөрөҫ түгел: ғәҙәттә[4], теләһә ниндәй декарт координаталар системаһында башҡарылған бәйләнештәргә генә «геометрик аңлатма биреп була» (инвариантлы) тип әйтәләр.
Векторҙар өҫтөндә ғәмәлдәр
[үҙгәртергә | сығанаҡты үҙгәртеү]Векторҙың модуле
[үҙгәртергә | сығанаҡты үҙгәртеү]векторының модуле тип киҫегенең оҙонлоғона тигеҙ булған һан атала. тип тамғалана. Координаталар аша ошолай иҫәпләнә:
Векторҙарҙы ҡушыу
[үҙгәртергә | сығанаҡты үҙгәртеү]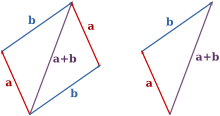
Координаталар аша күрһәткәндә, сумма векторы ҡушылыусыларҙың ярашлы координаталарын ҡушып табыла:
суммаһын геометрик төҙөү өсөн төрлө ҡағиҙәләр (ысулдар) ҡулланалар, ләкин улар бөтәһе лә бер үк һөҙөмтәне бирә. Теге йәки был ысулды ҡулланыу сығара торған мәсьәләгә нигеҙләнә.
Өсмөйөш ҡағиҙәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Өсмөйөш ҡағиҙәһе векторҙы күсеү булараҡ ҡарауҙан тәбиғи рәүештә килеп сыға. Ниндәйҙер нөктәгә ике һәм күсеүҙәрен эҙмә-эҙ башҡарыу һөҙөмтәһе, бер юлы күсеүен башҡарыу һөҙөмтәһе кеүек үк була икәне асыҡ күренә. Ике һәм векторҙарын өсмөйөш ҡағиҙәһе буйынса ҡушыу өсөн ике векторҙы ла, береһенең башы икенсеһенең осо менән тап килерлек итеп, үҙ-үҙҙәренә параллель күсерәләр. Ул саҡта сумма векторы барлыҡҡа килгән өсмөйөштөң өсөнсө яғы менән бирелә, шуның менән бергә уның башы беренсе векторҙың башы менән, ә осо икенсе векторҙың осо менән тап килә.
Был ҡағиҙә теләһә ниндәй һандағы векторҙарҙы ҡушыу өсөн, һыныҡ һыҙыҡ ҡағиҙәһенә күсеп, тура һәм тәбиғи рәүештә дөйөмләштерелә:
Күпмөйөш ҡағиҙәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Икенсе векторҙың башы беренсеһенең осо менән, өсөнсөһөнөң башы — икенсеһенең осо менән, һәм шулай артабан, тап килтерелә, векторҙың суммаһы, башы беренсе векторҙың башы менән, ә осо -сы векторҙың осо менән тап килгән вектор була (йәғни һыныҡ һыҙыҡты йомоусы йүнәлешле киҫек менән һүрәтләнә). Шулай уҡ һыныҡ һыҙыҡ ҡағиҙәһе тип атала.
Параллелограмм ҡағиҙәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Ике һәм векторҙарын параллелограмм ҡағиҙәһе буйынса ҡушыу өсөн, был ике векторҙы ла, уларҙың баштары тап килерлек итеп үҙ-үҙҙәренә параллель күсерәләр. Ул саҡта сумма векторы уларҙа төҙөлгән параллелограмдың, уларҙың уртаҡ башынан сыҡҡан диагонале менән күрһәтелә. (Был диагональ, өсмөйөш ҡағиҙәһен ҡулланғанда, өсмөйөштөң өсөнсө яғы менән тап килгәне күренеп тора).
Параллелограмм ҡағиҙәһе, сумма векторын шунда уҡ ике ҡушылыусы ла ҡуйылған нөктәгә һалынған итеп һүрәтләү кәрәк булғанда ҡулланыу уңайлы — йәғни өс векторҙы ла баштарын уртаҡ итеп һүрәтләргә кәрәк булғанда.
Векторҙар суммаһы модуле
[үҙгәртергә | сығанаҡты үҙгәртеү]Ике векторҙың суммаһы модулен косинустар теоремаһын ҡулланып иҫәпләргә була:
- , бында — һәм векторҙары араһындағы мөйөш косинусы.
Әгәр векторҙар өсмөйөш ҡағиҙәһенә ярашлы һүрәтләнһәләр һәм мөйөш һүрәттәгесә — ғәҙәттәге билдәләмә буйынса векторҙар араһындағы мөйөш менән тап килмәгән, өсмөйөштөң яҡтары араһында алынһа, тимәк килтерелгән формулалағы мөйөш менән дә тап килмәһә, ул саҡта һуңғы быуындың тамғаһы минус була.
Ирекле һандағы векторҙарҙың суммаһы өсөн оҡшаш формула ҡулланыла, унда косинуслы быуындар күберәк: сумма йыйылмаһынан һәр пар вектор өсөн берәр шундай быуын бар. Мәҫәлән, өс вектор өсөн формула ошолай:
Векторҙарҙы алыу
[үҙгәртергә | сығанаҡты үҙгәртеү]
Rоординаталар формаһында ике векторҙың айырмаһын табыу өсөн, векторҙарҙың ярашлы координаталарын алырға кәрәк:
Айырма векторын төҙөү өсөн векторҙарҙың башланғыс нөктәләрен тап килтерәләр һәм векторының башы векторының осо, ә осо — векторының осо була. Әгәр векторҙарҙың нөктәләрен ҡулланып яҙһаң, ул саҡта .
Векторҙарҙың айырмаһы модуле
[үҙгәртергә | сығанаҡты үҙгәртеү]Өс векторҙары, ҡушҡандағы кеүек, өсмөйөш төҙөйҙәр, һәм айырма модуле өсөн аңлатма оҡшаш килеп сыға:
бында — һәм векторҙары араһындағы мөйөш косинусы.
Сумма модуле формулаһынан айырма косинус алдындағы тамғала, шуның менән бергә ҡайһы мөйөш алынған икәнен яҡшы күҙәтергә кәрәк (өсмөйөш ҡағиҙәһе буйынса ҡушҡанда, сумма модуле формулаһының өсмөйөштөң яҡтары араһындағы мөйөш алынған варианты, бирелгән айырма модуле өсөн формуланан күренеше буйынса айырылмай, ләкин бында төрлө мөйөштәр алына икәнен күҙ уңында тоторға кәрәк: сумма осрағында векторы векторының осона күсерелгәндәге мөйөш алына, айырма модулен эҙләгәндә, бер нөктәгә ҡуйылған векторҙар араһындағы мөйөш алына; шул уҡ мөйөштө ҡулланғанда сумма модуле өсөн аңлатма, бирелгән айырма модуле өсөн аңлатмалағы кеүек, косинус алдындағы тамға менән генә айырыла).
Векторҙы һанға ҡабатлау
[үҙгәртергә | сығанаҡты үҙгәртеү]
векторын һанына ҡабатлау, оҙонлоғо тапҡыр ҙур булған, бер үк йүнәлешле вектор бирә.
векторын һанына ҡабатлау, оҙонлоғо тапҡыр ҙур булған, ҡапма-ҡаршы йүнәлешле вектор бирә.
Координаталар формаһында векторҙы һанға ҡабатлау, векторҙың бөтә координаталарын был һанға ҡабатлап башҡарыла:
Билдәләмәнән сығып һанға ҡабатланған векторҙың модуле өсөн аңлатма килеп сыға:
Һандар өҫтөндәге ғәмәлдәргә оҡшаш рәүештә, векторҙы үҙ-үҙенә ҡушыу ғәмәлен һанға ҡабатлау ғәмәле аша яҙырға мөмкин:
Ә векторҙарҙы алыу ғәмәлен ҡушыу һәм ҡабатлау аша яҙырға мөмкин:
-гә ҡабатлау векторҙың оҙонлоғон үҙгәртмәй, тик йүнәлешен генә үҙгәртә икәндән сығып, һәм векторҙың билдәләмәһен иҫәпкә алып, табабыҙ:
Бында форматланмаған тексты өҫтәгеҙ.=== Векторҙарҙың скаляр ҡабатландығы ===
Геометрик векторҙар өсөн скаляр ҡабатландыҡҡа билдәләмә уларҙың геометрик характеристикалары аша бирелә һәм түбәндәгесә индерелә:
Бында косинусты иҫәпләү өсөн векторҙар араһындағы мөйөш алына, ул, әгәр векторҙарҙы бер нөктәнән һалһаң (баштарын тап килтерһәң), векторҙар төҙөгән мөйөш дәүмәле тип билдәләнә.
Был аңлатманы координаталар аша яҙырға мөмкин (бында өс үлсәмле арауыҡ өсөн формула):
Векторҙың скаляр квадраты тип векторҙың үҙ-үҙенә скаляр ҡабатландығы атала һәм векторҙың модуле аша иҫәпләнергә мөмкин:
Векторҙарҙың векторлы ҡабатландығы
[үҙгәртергә | сығанаҡты үҙгәртеү]Ике һәм векторҙарының векторлы ҡабатландығы тип һәм векторҙары яҫылығына ортогональ, оҙонлоғо векторҙар төҙөгән параллелограмдың майҙанына тигеҙ булған, ә йүнәлеше уң ҡул ҡағиҙәһе буйынса билдәләнгән векторы атала.
Векторҙарҙың ҡатнаш ҡабатландығы
[үҙгәртергә | сығанаҡты үҙгәртеү]Өс векторҙарының ҡатнаш ҡабатландығы тип түбәндәгесә билдәләнгән һан атала:
Был дәүмәлдең модуле векторҙарында төҙөлгән параллелепипедтың күләмен бирә.
Шулай уҡ ҡарағыҙ
[үҙгәртергә | сығанаҡты үҙгәртеү]Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
- Башмаков М. Что такое вектор? (рус.) // Квант. — 1976. — № 4. — С. 2—5.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия 7-9 классы. — Москва: Просвещение, 2010. — 384 с. — ISBN 978-5-09-023915-8.
- ↑ Элементарная математика, 1976, с. 249.
- ↑ 3,0 3,1 Выгодский М. Я. Справочник по высшей математике. — Москва: Астрель, 2006. — 991 с. — ISBN 5-271-03651-0.
- ↑ Это утверждение, очевидно, до некоторой степени условно, поскольку конкретная фиксированная система координат при желании может быть явно включена в число объектов, для которых соотношения устанавливаются, и тогда алгебраические утверждения для этой фиксированной частной системы координат могут быть переформулированы так, что будут инвариантными при записи в любой другой, произвольной, системе координат.





























































