Алгоритм

Алгоритм
	Алгоритм
Кем хөрмәтенә аталған	Әл-Хәрәзми
Етештереү ысулы	алгоритмизация[d]
Вики-проект	Проект:Информационные технологии[d] һәм Проект:Математика[d]
EntitySchema для класса	Ошибка Lua в Модуль:Wikidata на строке 301: Неизвестный тип сущности..
	Алгоритм Викимилектә

Математикала һәм компьютер фәндәрендә алгоритм (фарсы телендә خوارزمی [al-Khwārazmī]) — этаплап иҫәпләү процедураһы. Анығыраҡ әйткәндә, алгоритм — мәсьәләне сисеүҙең аныҡ күрһәтмәләрҙән торған сикле теҙмә рәүешендә сағылдырылған ысулы. Алгоритм ярҙамында иҫәпләү процедураһы башланғыс күрһәтмәнән кереү мәғлүмәттәре менән башланып, башҡарылыу барышында эҙмә-эҙлекле аныҡ күрһәтмәләр аша үтә һәм, аҙаҡта сығыу мәғлүмәттәре булдырып, һуңғы күрһәтмәлә тамамлана.

Алгори́тм (лат. algorithmi — Урта Азия математигы Әл-Хәрәзми исеменән алынған^[1]) — билдәле бер мәсьәләне сығарыу өсөн башҡарыусының эш итеү тәртибен тасуирлаусы, ҡайһы бер класс мәсьәләләрен сығарыуҙың аныҡ ҡағиҙәләренән торған сикле йыйылма йәки күрһәтмәләр йыйынтығы. Иҫке трактовкала «тәртип» һүҙе урынына «эҙмә-эҙлеклек» һүҙе ҡулланыла, компьютерҙар эшендә параллеллек үҫешкән һайын «эҙмә-эҙлеклек» һүҙе дөйөмерәк «тәртип» һүҙе менән алмаштырыла башлай. Ирекле инструкциялар, әгәр ҡулланылған башҡарыусылар мөмкинлек бирһә, ирекле тәртиптә, параллель башҡарыла алалар.

Элегерәк рус телендә «алгорифм» тип яҙғандар, хәҙер ундай яҙыу һирәк ҡулланыла, шулай булыуға ҡарамаҫтан ташлама ғәмәлдә (Марковтың нормаль алгорифмы]]).

Йыш ҡына башҡарыусы сифатында компьютер сығыш яһай, ләкин алгоритм төшөнсәһе компьютер программаларына ғына ҡағылмай, шулай, мәҫәлән, аныҡ тасуирланған ашамлыҡ әҙерләү ысулы шулай уҡ алгоритм була, был осраҡта башҡарыусы булып кеше тора (ә бәлки ниндәйҙер механизм, мәҫәлән һанлы идара ителеүсе туҡыу станогы, һәм башҡалар).

Иҫәпләү алгоритмдарын (артабан һүҙ күберәк шулар тураһында бара), һәм идара итеү алгоритмдарын айырып ҡарарға була. Иҫәпләү алгоритмдары ниндәйҙер функцияны иҫәпләүҙе башҡарып, бирелгән башланғыс мәғлүмәттәрҙе сығыу мәғлүмәттәренә үҙгәртәләр. Идара итеү алгоритмдарының семантикаһы тулыһынса айырыла һәм билдәләнгән ваҡыттарҙа йәки тышҡы ваҡиғаларға реакция сифатында тейешле идара итеүсе ғәмәлдәр сығарыуға ҡайтарылып ҡалдырылырға мөмкин (был осраҡта, иҫәпләү алгоритмынан айырмалы рәүештә, идара итеү алгоритмы сикһеҙ башҡарыу ваҡытында рөхсәт ителә торған булып ҡалырға мөмкин).

Алгоритм төшөнсәһе математиканың төп, башланғыс төшөнсәләре иҫәбенә керә. Алгоритмик характерҙағы иҫәпләү процестары (бөтөн һандар өҫтөндә арифметик ғәмәлдәр, ике һандың иң ҙур уртаҡ бүлеүсеһен табыу һәм башҡалар) кешелеккә борондан билдәле булған. Шулай ҙа был төшөнсә XX быуат башында ғына асыҡтан-асыҡ формалаша.

Алгоритм төшөнсәһен өлөшләтә формалләштереү, Давид Гильберт 1928 йылда формулировкалаған хәл итеү проблемаһын хәл итергә маташыуҙарҙан башлана (нем. Entscheidungsproblem). Формалләштереүҙең артабанғы этаптары эффектив иҫәпләүҙәрҙе^[2] йәки «эффектив ысулдарҙы»^[3] билдәләү өсөн кәрәк була; шундай формалләштереүҙәр араһында — Гёдель — Эрбран — Клиниҙың рекурсив функциялары 1930, 1934 һәм 1935 йй., Алонзо Чёрчтың λ-иҫәпләмәһе 1936 й., Эмиль Посттың 1936 йылдағы «формулировка 1-е» һәм Тьюринг машинаһы.

Алгоритмдың билдәләмәләре

Алгоритмдарҙың үҙсәнлектәре

Алгоритмдың төрлө билдәләмәләренә асыҡ йәки асыҡ булмаған формала түбәндәге бер нисә дөйөм талаптар ҡуйыла:

Дискретлыҡ — алгоритм мәсьәләне сығарыу процесын ҡайһы бер ябай аҙымдарҙы билдәле бер тәртиптә башҡарыу итеп күрһәтергә тейеш. Шуның менән бергә алгоритмдың һәр аҙымын башҡарыу өсөн сикле ваҡыт арауығы талап ителә, йәғни сығанаҡ мәғлүмәттәрен һөҙөмтәгә әйләндереү ваҡытта дискрет башҡарыла.
Детерминирланғанлыҡ (аныҡлыҡ). Һәр ваҡыт эштең артабанғы этабы системаның торошо менән бер төрлө билдәләнә. Шул рәүешле, бер үк сығанаҡ мәғлүмәт өсөн алгоритм бер үк һөҙөмтә (яуап) сығара. Хәҙерге заман трактовкаһында бер үк алгоритмдың төрлө тормошҡа ашырылышында изоморфлы графа булырға тейеш. Икенсе яҡтан, ихтимал алгоритмдар бар, уларҙа киләһе аҙым системаның хәҙерге торошона һәм барлыҡҡа килгән осраҡлы һанға бәйле. Әммә осраҡлы һандар барлыҡҡа килеү ысулын «сығанаҡ мәғлүмәттәр» исемлегенә индергәндә ихтималлы алгоритм ғәҙәттәгенең аҫтөрө булып китә.
Аңлайышлы булыу — алгоритм башҡарыусы үтәй алған һәм уның командалар системаһына ингән командаларҙы ғына индерергә тейеш.
Тамамланыусанлыҡ (сиклелек) — алгоритмдың математик функция кеүек тар мәғәнәһендә, дөрөҫ бирелгән сығанаҡ мәғлүмәттәр өсөн алгоритм эште тамамларға һәм билдәле бер һандағы аҙымдан һуң яуап сығарырға тейеш. Дональд Кнут алгоритмдың, бәлки, сиклелектән башҡа бөтә үҙсәнлектәрен ҡәнәғәтләндергән процедураны иҫәпләү ысулы тип атай(ингл. computational method)^[4]. Ләкин йыш ҡына алгоритм билдәләмәһе сикле ваҡыт эсендә тамамланыусанлыҡты индермәй^[5]. Был осраҡта алгоритм (иҫәпләү ысулы) өлөшсә функцияны^[en] билдәләй. Ихтимал алгоритмдар өсөн тамамланғанлыҡ (тулылыҡ), ҡағиҙә булараҡ, алгоритм теләһә ниндәй дөрөҫ күрһәтелгән башланғыс мәғлүмәттәр өсөн 1 ихтималлыҡ менән һөҙөмтә бирә тигәнде аңлата (йәғни ҡайһы бер осраҡтарҙа ул тамамланмай ҡалырға мөмкин, әммә бының ихтималлығы 0 булырға тейеш).
Киң таралғанлыҡ (универсаллек). Алгоритм башланғыс мәғлүмәттәрҙең төрлө йыйылмаһына ҡулланырлыҡ булырға тейеш.
Һөҙөмтәлелек — алгоритмдың билдәле бер һөҙөмтә менән тамамланыуы.

Формаль билдәләмә

Математиканың төрлө теоретик проблемалары һәм физика һәм техниканың үҫешенең тиҙләнеше алгоритм төшөнсәһенең аныҡ билдәләмәһен биреүҙе талап итә.

Алгоритм төшөнсәһен беренсе аныҡларға маташыуҙар һәм уны өйрәнеү X быуаттың беренсе яртыһында Алан Тьюринг, Эмиль Пост, Жак Эрбран, Курт Гедель, А. А. Марков, Алонзо Чёрч тарафынан башҡарыла. Алгоритм төшөнсәһенең бер нисә билдәләмәһе эшләнә, аҙаҡтан уларҙың бөтәһенең дә бер үк төшөнсәне билдәләгәне асыҡлана (ҡарағыҙ. Тезис Чёрча — Тьюринга)^[6]

Рәсәй математигы, Советтар Союзында структуралы лингвистикаға нигеҙ һалған В. А. Успенский алгоритм төшөнсәһе иң беренсе Эмиль Борелдең 1912 йылда аныҡ интеграл тураһында мәҡәләһендә күренә тип иҫәпләй. Унда ул «тормошҡа ашырырға мөмкин булған иҫәпләүҙәр» тураһында яҙа, шул уҡ ваҡытта: «Мин аңлы рәүештә күберәк йәки әҙерәк практик эшмәкәрлекте ситтә ҡалдырам; асылы шунда, был операцияларҙың һәр береһе сикле ваҡыт эсендә ышаныслы һәм ике мәғәнәле булмаған ысулдар менән башҡарыла алалар» тип һыҙыҡ өҫтөнә ала^[7].

Тьюринг машинаһы

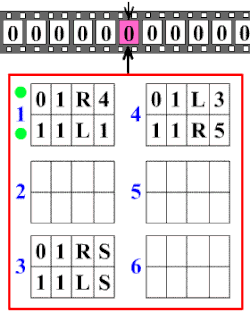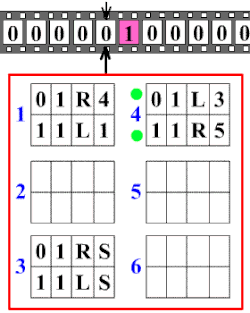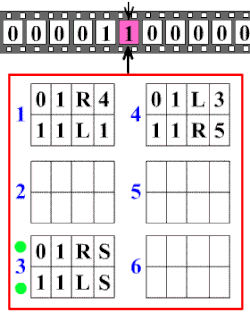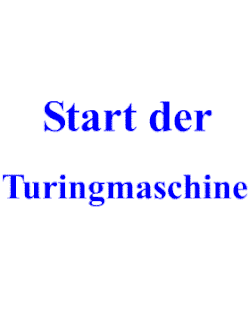
Тьюринг машинаһының нигеҙендә ятҡан төп идея бик ябай. Тьюринг машинаһы — ул символдар яҙылған айырым күҙәүҙәр таҫмаһы менән эшләүсе абстракт машина (автомат). Машинаның шулай уҡ күҙәүҙәрҙәге символдарҙы яҙыу һәм уҡыу өсөн таҫма буйлап хәрәкәт итә алған башы (головка) бар. Һәр аҙымында машина баш күрһәткән күҙәүҙәге символды уҡый, һәм, уҡылған символ һәм эске торошо нигеҙендә артабанғы аҙымын яһай. Шул уҡ ваҡытта машина үҙенең торошон үҙгәртергә, күҙәүгә икенсе символ яҙырға, йәки башын бер күҙәүгә уңға йәки һулға күсерергә мөмкин^[8]

Был машиналарҙы тикшереү нигеҙендә Тьюринг тезисы тәҡдим ителә (алгоритдарҙың төп гипотезаһы):

Ниндәйҙер алфавитта бирелгән функцияның ҡиммәттәрен табыу өсөн ниндәйҙер алгоритм, функция Тьюринг буйынса иҫәпләнгәндә генә һәм бары тик шул саҡта, йәғни уны Тьюринг машинаһында иҫәпләп булғанда ғына була.

Был тезис аксиома, постулат булып тора, һәм математик ысулдар менән иҫбат ителә алмай, сөнки алгоритм аныҡ математик төшөнсә түгел.

Рекурсив функциялар

Төп мәҡәлә: Рекурсив функция (иҫәпләнеүсәнлек теорияһы)

Һәр алгоритм менән ул иҫәпләгән функцияны ярашлы ҡуйып була. Әммә ирекле функцияға Тьюринг машинаһын ярашлы ҡуйып буламы тигән һорау тыуа, ә әгәр булмаһа, ниндәй функциялар өсөн алгоритм бар? Ошо һорауҙарҙы тикшереү 1930-сы йылдарҙ рекурсив функциялар теорияһына килтерә^[9].

Иҫәпләнмәле функциялар класы аксиомалар системаһы нигеҙендә ниндәйҙер аксиоматик теорияны төҙөүҙе хәтерләткән һында яҙыла. Башта иҫәпләүе күҙгә күренеп торған иң ябай функциялар һайлап алына. Аҙаҡ булған функциялар нигеҙендә яңы функцияларҙы төҙөү ҡағиҙәләре (операторҙар) әйтеп бирелә. Кәрәкле функциялар класы иң ябай функцияларҙан операторҙарҙы ҡулланып алып була торған бөтә функцияларҙан тора.

Тьюринг тезисына оҡшаш рәүештә иҫәпләнмәле функциялар теорияһында Чёрч тезисы тип аталған гипотеза тәҡдим ителә:

Һанлы функция өлөшләтә рекурсив булғанда ғына һәм бары тик шул саҡта ғына алгоритм ярҙамында иҫәпләнә.

Иҫәпләнмәле функциялар класы Тьюринг буйынса иҫәпләнеүселәр менән тап килеүен иҫбатлау ике аҙымда башҡарыла: тәүҙә иң ябай функцияларҙың Тьюринг машинаһында иҫәпләнеүен, ә аҙаҡ — операторҙар ҡулланыу һөҙөмтәһендә алынған функцияларҙың иҫәпләнеүен иҫбатлайҙар.

Шулай итеп, формаль булмаған рәүештә алгоритм, әгәр ул булһа, сикле һандағы аҙымдан һуң тәүге мәғлүмәттәрҙән (индереүҙә) эҙләнгән һөҙөмтәгә (сығарыуҙа) алып барыусы дискрет детерминистик процесты билдәләүсе аныҡ инструкциялар системаһы тип билдәләнә ала; әгәр эҙләнгән һөҙөмтә булмаһа, алгоритм йә бер ҡасан да эште тамамламай, йәки аптырап ҡала.

Марковтың нормаль алгоритмы (алгорифм)

Төп мәҡәлә: Нормальный алгоритм

Марковтың нормаль алгоритмы (автор яҙыуында алгорифм) — ул билдәле бер алфавит символдарынан төҙөлгән төп һүҙҙәрҙән яңы һүҙҙәр алыуҙың билдәле бер процедураларын тормошҡа ашырыусы алмаштырыуҙарҙы эҙмә-эҙлекле ҡулланыу системаһы. Тьюринг машинаһы кеүек үк, нормаль алгоритмдар иҫәпләүҙәрҙең үҙҙәрен башҡармайҙар: улар тик хәрефтәрҙе бирелгән ҡағиҙәләр буйынса алмаштырыу юлы менән һүҙҙәрҙе үҙгәртеүҙе башҡаралар^[10].

Нормаль иҫәпләнмәле тип нормаль алгоритм менән башҡарырға мөмкин булған функцияны атайҙар. Йәғни функцияның мөмкин булған бирелештәр күмәклегенән һәр һүҙҙе уның тәүге ҡиммәтенә үҙгәртеүсе алгоритм^[11]..

Нормаль алгоритмдар теорияһын төҙөүсе А. А. Марков, Марковтың нормалләштереү принцибы тип аталған гипотезаны тәҡдим итә:

Ниндәйҙер алфавитта бирелгән функцияның ҡиммәттәрен табыу өсөн, функция нормаль иҫәпләнмәле булғанда ғына һәм бары тик шул саҡта ғына ниндәйҙер алгоритм бар.

Тьюринг һәм Черчтың тезистарына оҡшаш рәүештә, Марковтың нормалләштереү принцибы математик ысулдар менән иҫбатлана алмай.

Стохастик алгоритмдар

Юғарыла килтерелгән алгоритмдың формаль билдәләмәһе ҡайһы бер осраҡтарҙа үтә ҡәтғи булырға мөмкин. Ҡайһы берҙә осраҡлы дәүмәлдәрҙе ҡулланыу кәрәклеге килеп тыуа^[12]. Баштағы бирелештәр менән генә түгел, Ҡалып:D-l алынған ҡиммәттәр менән дә эшләүсе алгоритм стохастик алгоритм тип атала^[13]. Формаль рәүештә ундай алгоритмдарҙы алгоритм тип атарға ярамай, сөнки стохастик алгоритмдар йыш ҡына детерминирланғандарҙан нәтижәлерәк булалар, ә айырым осраҡтарҙа — мәсьәләне сисеүҙең берҙән-бер ысулы^[12].

Практикала осраҡлы һандар генераторы урынына псевдо-осраҡлы һандар генераторы ҡулланыла.

Әммә стохастик алгоритмдарҙы һәм юғары ихтималлыҡ менән дөрөҫ нәтижә биреүсе ысулдарҙы айырып ҡарарға кәрәк. Ысулдан айырмалы рәүештә, алгоритм хатта оҙаҡ эшләгәндән һуң да дөрөҫ һөҙөмтәләр бирә.

Ҡайһы бер тикшеренеүселәр стохастик алгоритмдың алдан билдәле булған ниндәйҙер ихтималлыҡ менән дөрөҫ булмаған һөҙөмтә биреү мөмкинлеген таный. Ул саҡта стохастик алгоритмдарҙы ике төргә бүлергә мөмкин^[14]:

Лас-Вегас тибындағы алгоритмдар һәр саҡ дөрөҫ нәтижә бирәләр, тик уларҙың эш ваҡыты билдәләнмәгән.
Монте-Карло тибындағы алгоритмдар, алдағыларҙан айырмалы рәүештә, билдәле ихтималлыҡ менән дөрөҫ булмаған һөҙөмтә бирергә мөмкиндәр.

Башҡа формализациялар

Ҡайһы бер мәсьәләләр өсөн юғарыла аталған формализациялар сығарылышын эҙләүҙе һәм тикшеренеүҙәрҙе тормошҡа ашырыуҙы ҡыйынлаштырырға мөмкиндәр. Ҡаршылыҡтарҙы еңеп сығыу өсөн «классик» схемаларҙың модификациялары эшләнә, шулай уҡ алгоритмдарҙың яңы моделдәре булдырыла. Атап китергә мөмкин:

Тьюрингтың күп таҫмалы һәм детерминирланмаған машинаһы;
регистрлы һәм РАМ-машина — заманса компьютерҙарҙың һәм виртуаль машиналарҙың прототибы;
сикле һәм күҙәнәкле автоматтар

Алгоритм төрҙәре

Логик-математик сара булараҡ алгоритмдарҙың төрҙәре кеше эшмәкәрлегенең күрһәтелгән компоненттарын һәм йүнәлештәрен сағылдыра, ә алгоритмдар үҙҙәре маҡсатҡа, мәсьәләнең башланғыс шарттарына, уны хәл итеү юлдарына бәйле. Ниндәйҙер кереү мәғлүмәттәрен сығыу мәғлүмәттәренә үҙгәртеүсе иҫәпләү характерындағы алгоритмдар (юғарыла телгә алынған Тьюринг, Пост, РАМ машиналары, Марковтың нормаль алгорифмдары һәм рекурсив функциялар тап шуларҙың формализацияһы булып торалар) һәм логик идара итеү алгоритмдары тип аталған интерактив алгоритмдар араһында принципиаль айырманы һыҙыҡ өҫтөнә алырға кәрәк (Тьюрингтың C-машинаһы барлыҡҡа килә, ингл. choice һүҙенән — һайлау, бөтә башланғыс мәғлүмәттәре иҫәпләү башланғансы уҡ бирелгән һәм сығыу мәғлүмәттәре иҫәпләү тамамланғансы билдәһеҙ булған классик A-машинанан айырмалы рәүештә, тышҡы тәьҫир көтә). Һуңғылары ниндәйҙер идара итеү объекты менән үҙ-ара тәьҫир итешеү өсөн һәм идара итеү объектынан килгән сигналдар сағылдырылған килеп тыуған хәлгә ҡарап дөрөҫ идара итеүсе йоғонто яһауҙы тәьмин итеү өсөн тәғәйенләнгәндәр^[15]^[16]. Ҡайһы бер осраҡтарҙа идара итеү алгоритмы эштең тамамланыуын бөтөнләй күҙ уңында тотмай (мәҫәлән, ярашлы реакция бирелгән ваҡиғаларҙы көтөүҙең сикһеҙ циклын алып бара), шуға ҡарамаҫтан, тулыһынса дөрөҫ була.

Ошондай алгоритмдарҙы айырып күрһәтергә мөмкин:

Механик алгоритмдар, йәки икенсе төрлө детерминирланған, ҡаты (мәҫәлән, машинаның, двигателдең һәм башҡаларҙың эш алгоритмы) — билдәле бер ғәмәлдәрҙе бирәләр, уларҙы берҙән-бер һәм дөрөҫ эҙмә-эҙлелектә билдәләп, шуның менән, әгәр, алгоритм эшләнгән процестың, мәсьәләнең шарттары үтәлһә, аныҡ талап ителгән йәки эҙләнгән һөҙөмтәне тәьмин итәләр.
Һығылмалы алгоритмдар, мәҫәлән, стохастик, йәғни ихтималла һәм эвристик.
Ихтималлы (стохастик) алгоритм мәсьәләне бер нисә юл йәки ысул менән мөмкин булған һөҙөмтәгә өлгәшеүгә килтереүсе хәл итеү программаһын бирә.
Эвристик алгоритм («эврика» тигән грек һүҙенән) — ҡәтғи нигеҙләмәйенсә төрлө төплө фекерҙәр ҡулланған алгоритм^[17].
Һыҙыҡлы алгоритм — эҙмә-эҙлекле рәүештә бер-бер артлы үтәлгән командалар (күрһәтмәләр) йыйылмаһы
Тармаҡланыусы алгоритм — кәм тигәндә бер шарт ингән алгоритм, был шартты тикшереү һөҙөмтәһендә алгоритмдың бер нисә альтернатив тармаҡҡа бүленеүе мөмкин.
Цикллы алгоритм — бер үк ғәмәлде (бер үк операцияларҙы) бер нисә тапҡыр ҡабатлауҙы күҙ уңында тотҡан алгоритм. Иҫәпләү, варианттарҙы берәмтекләп ҡарау ысулдарының күбеһе цикллы алгоритмдарға ҡайтып ҡала. Программаның циклы — күп тапҡыр башҡарылырға мөмкин булған командалар эҙмә-эҙлелеге (серия, циклдың есеме).
Ярҙамсы (ҡул аҫтындағы) алгоритм (процедура) — элек эшләнгән һәм теге йәки был мәсьәләне алгоритмлаштырыуҙа тулыһынса ҡулланылған алгоритм. Ҡайһы бер осраҡтарҙа төрлө бирелештәр өсөн бер үк күрһәтмәләр (командалар) эҙмә-эҙлелеге булһа, яҙманы кәметеү маҡсатында шулай уҡ ярҙамсы алгоритм бүленә. Проблеманы алгоритмлаштырыуға әҙерлектең бөтә этаптарында ла алгоритмдың структур сағылышы киң ҡулланыла.
Структуралы блок-схема, алгоритмдың граф-схемаһы — алгоритмдың уҡтар (күсеү юлдары) ярҙамында бер-береһенә тоташтырылған, һәр береһе алгоритмдың бер аҙымына тап килгән блоктар— график символдар схемаһы рәүешендәге график һүрәте. Блок эсендә тейешле ғәмәлдең тасуирламаһы бирелә. Алгоритмдың график һүрәте, күргәҙмәле булыуы арҡаһында, мәсәләне программалау алдынан киң ҡулланыла, сөнки күреү аша үҙләштереү, ҡағиҙә булараҡ, программаны яҙыу процесын, мөмкин булған хаталар осрағында уны төҙәтеүҙе, мәғлүмәтте эшкәртеү процесын аңлауҙы еңеләйтә. Хатта ошондай әйтемде осратырға мөмкин: «Тышҡы яҡтан алгоритм — схема — тура дүртмөйөштәр һәм башҡа символдар йыйылмаһы, уның эсендә нимә хисаплана, машинаға нимә индерелгәне һәм баҫма өсөн нимә сығарылғаны һәм мәғлүмәтте күрһәтеүҙең башҡа саралары яҙыла».

Алгоритмдарҙың номерҙары

Алгоритмдарҙы номерлау уларҙы тишереүҙә һәм анализлауҙа мөһим роль уйнай^[18]. Теләһә ниндәй алгоритмды сикле һүҙ рәүешендә бирергә (ниндәйҙер алфавит символдарының сикле эҙмә-эҙлелеге рәүешендә күрһәтергә) мөмкин булғанлыҡтан, ә сикле алфавитта бөтә сикле һүҙҙәр күмәклеге иҫәпләмәле, бөтә алгоритмдар күмәклеге лә шулай уҡ иҫәпләмәле. Был бөтә натураль һандар күмәклеге һәм алгоритмдар күмәклеге араһында үҙ-ара бер ҡиммәтле сағылыш барлығын, йәғни һәр алгоритмға номер биреү мөмкинлеген аңлата.

Алгоритмдарҙы номерлау является бер үк ваҡытта бөтә алгоритм ярҙамында иҫәпләнмәле функцияларҙы ла номерлау булып тора, шуның менән бергә теләһә ниндәй функцияның сикһеҙ күп һанда номеры булырға мөмкин.

Номерлауҙы булдырыу алгоритмдар менән һандар менән эш иткән кеүек эшләргә мөмкинлек бирә. Номерлау бигерәк тә башҡа алгоритмдар менән эшләгән алгоритмдарҙы тикшергәндә файҙалы.

Миҫал

Евклид алгоритмы — иң ҙур уртаҡ бүлеүсене (ИҘУБ) иҫәпләүҙең эффектив ысулы. Грек математигы Евклид хөрмәтенә аталған; иң боронғо алгоритмдарҙың береһе, ул әле булһа ҡулланыла^[19].

Евклидтың "Башланғыстар"ында (яҡынса б. э. т. 300 йыл), атап әйткәндә, VII һәм X китаптарында тасуирланған. Етенсе китабында бөтөн һандар өсөн, ә унынсы китабында — киҫек оҙонлоҡтары өсөн алгоритм.

Алгоритмдың бер нисә варианты бар, түбәндә псевдокодта яҙылған рекурсив варианты:

функция ИҘУБ(a, b)
    әгәр b = 0
       әйләнеп ҡайтырға ә
    кире осраҡта
       әйләнеп ҡайтырға ИҘУБ (b, a mod b)

1599 һәм 650 һандарының ИҘУБ-ы:

Аҙым 1	1599 = 650*2 + 299
Аҙым 2	650 = 299*2 + 52
Аҙым 3	299 = 52*5 + 39
Аҙым 4	52 = 39*1 + 13
Аҙым 5	39 = 13*3 + 0

Шулай уҡ ҡарағыҙ

Иҫкәрмәләр

↑ Семёнов А. Л. АЛГОРИТМ (билдәһеҙ). Большая российская энциклопедия. Электронная версия (2016). Дата обращения: 29 октябрь 2018. 2018 йыл 30 октябрь архивланған.
↑ Kleene 1943 in Davis 1965: 274
↑ Rosser 1939 in Davis 1965: 225
↑ Кнут, 2006, 1.1. Алгоритмы
↑ Robert Andrew Wilson, Frank C. Keil. The MIT Encyclopedia of the Cognitive Sciences. — MIT Press, 2001. — С. 11. — 1106 с. — ISBN 9780262731447.
↑ (Игошин, с. 317)
↑ В. А. Успенский: «Математика — это гуманитарная наука» (рус.) // Троицкий вариант. — 2014. — № 2(146). — С. 4—6.
↑ Basics: The Turing Machine (with an interpreter!) (билдәһеҙ). Good Math, Bad Math (9 февраль 2007). Архивировано 2 февраль 2012 года. 2012 йыл 11 февраль архивланған.
↑ (Игошин, раздел 33)
↑ Энциклопедия кибернетики, т. 2, c. 90—91.
↑ (Игошин, раздел 34)
↑ ^12,0 ^12,1 «Probabilistic algorithms should not be mistaken with methods (which I refuse to call algorithms), which produce a result which has a high probability of being correct. It is essential that an algorithm produces correct results (discounting human or computer errors), even if this happens after a very long time». Henri Cohen. A Course in Computational Algebraic Number Theory (инг.). — Springer-Verlag, 1996. — P. 2. — ISBN 3-540-55640-0.
↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rives't, Clifford Stein. Introduction to Algorithms (инг.). — 2-е. — MIT Press, 2001. — P. 531. — ISBN 0-262-03293-7.
↑ (Раздел 12, с. 12—22 в Atallah, 2010)
↑ Dina Goldin, Peter Wegner. The origins of the Turing Thesis Myth, CS-04-14, October 2004
↑ Interactive Computation Is More Powerful Than Non Interactive, c2.com
↑ М. Гэри, Д. Джонсон, Вычислительные машины и труднорешаемые задачи, М.: Мир, 1982, C. 155.
↑ (Игошин, раздел 36)
↑ Knuth D. The Art of Computer Programming, Volume 2: Seminumerical Algorithms (инг.). — 3rd. — Addison–Wesley, 1997. — ISBN 0201896842.

Әҙәбиәт

Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms, Third Edition. — 3-е. — М.: «Вильямс», 2013. — 1328 с. — ISBN 978-5-8459-1794-2.
Дональд Кнут. Искусство программирования = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд.. — М.: «Вильямс», 2006. — Т. 1. Основные алгоритмы. — С. 720. — ISBN 0-201-89683-4.
Томас Х. Кормен. Алгоритмы: вводный курс = Algorithms Unlocked. — М.: «Вильямс», 2014. — 208 с. — ISBN 978-5-8459-1868-0.
Игошин В. И. Математическая логика и теория алгоритмов. — 2-е изд., стер.. — М.: ИЦ «Академия», 2008. — 448 с. — ISBN 5-7695-1363-2.

[1] Семёнов А. Л. АЛГОРИТМ (билдәһеҙ). Большая российская энциклопедия. Электронная версия (2016). Дата обращения: 29 октябрь 2018. 2018 йыл 30 октябрь архивланған.

[2] Kleene 1943 in Davis 1965: 274

[3] Rosser 1939 in Davis 1965: 225

[Кнут—2006—1.1._Алгоритмы—-4] Кнут, 2006, 1.1. Алгоритмы

[5] Robert Andrew Wilson, Frank C. Keil. The MIT Encyclopedia of the Cognitive Sciences. — MIT Press, 2001. — С. 11. — 1106 с. — ISBN 9780262731447.

[6] (Игошин, с. 317)

[7] В. А. Успенский: «Математика — это гуманитарная наука» (рус.) // Троицкий вариант. — 2014. — № 2(146). — С. 4—6.

[gmbm-8] Basics: The Turing Machine (with an interpreter!) (билдәһеҙ). Good Math, Bad Math (9 февраль 2007). Архивировано 2 февраль 2012 года. 2012 йыл 11 февраль архивланған.

[9] (Игошин, раздел 33)

[10] Энциклопедия кибернетики, т. 2, c. 90—91.

[11] (Игошин, раздел 34)

[cohen1996-12] 12,0 ^12,1 «Probabilistic algorithms should not be mistaken with methods (which I refuse to call algorithms), which produce a result which has a high probability of being correct. It is essential that an algorithm produces correct results (discounting human or computer errors), even if this happens after a very long time». Henri Cohen. A Course in Computational Algebraic Number Theory (инг.). — Springer-Verlag, 1996. — P. 2. — ISBN 3-540-55640-0.

[mit-13] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rives't, Clifford Stein. Introduction to Algorithms (инг.). — 2-е. — MIT Press, 2001. — P. 531. — ISBN 0-262-03293-7.

[14] (Раздел 12, с. 12—22 в Atallah, 2010)

[15] Dina Goldin, Peter Wegner. The origins of the Turing Thesis Myth, CS-04-14, October 2004

[16] Interactive Computation Is More Powerful Than Non Interactive, c2.com

[17] М. Гэри, Д. Джонсон, Вычислительные машины и труднорешаемые задачи, М.: Мир, 1982, C. 155.

[18] (Игошин, раздел 36)

[knuth2-19] Knuth D. The Art of Computer Programming, Volume 2: Seminumerical Algorithms (инг.). — 3rd. — Addison–Wesley, 1997. — ISBN 0201896842.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]