Логарифм
һанының нигеҙе буйынса логарифмы (бор. грек. λόγος «һүҙенән; сағыштырма» + ἀριθμός «һан»[1]) һанын табыу өсөн нигеҙен күтәрергә кәрәк булған дәрәжә күрһәткесе булараҡ билдәләнә[2]. Тамғалау: , « нигеҙе буйынса һанының логарифмы» тип уҡыла.
Билдәләмәнән күренеүенсә, -ты табыу тигеҙләмәһен сығарыуға тиң көслө. Мәҫәлән, , сөнки .
Логарифмды иҫәпләү логарифмлау тип атала. һандары йышыраҡ ысын һандар, ләкин шулай уҡ комплекслы логарифмдар теорияһы ла бар ![]() .
.
Логарифмдар, күп хеҙмәт талап иткән иҫәпләүҙәрҙе һиҙелерлек ябайлаштырыу өсөн киң ҡулланылышын тәьмин иткән, уникаль үҙсәнлектәргә эйә[3]. «Логарифмдар донъяһына» күскәндә, ҡабатлау күпкә ябайыраҡ булған ҡушыу менән алмаштырыла, бүлеү — алыуға, ә дәрәжәгә күтәреү һәм тамыр алыу ярашлы рәүештә дәрәжә күрһәткесенә ҡабатлау һәм бүлеүгә әйләнә. Лаплас, логарифмдарҙы уйлап табыу, «астрономдың хеҙмәтен ҡыҫҡартып, уның ғүмерен ике тапҡыр оҙайтты» тип әйткән[4].
Логарифмдың билдәләмәһен һәм уларҙың ҡиммәттәре таблицаһын (тригонометрик функциялар өсөн) беренсе тапҡыр 1614 йылда шотланд математигы Джон Непер баҫтырып сығара. Башҡа математиктар тарафынан киңәйтелгән һәм аныҡлыҡ индерелгән логарифмик таблицалар, электрон калькуляторҙар һәм компьютерҙар барлыҡҡа килгәнгә тиклем, өс быуаттан артыҡ ваҡыт бөтә урында фәнни һәм инженер иҫәпләүҙәрендә ҡулланылалар.
Ваҡыт үтеү менән, логарифмлы функцияһы кеше эшмәкәрлегенең башҡа күп өлкәләрендә лә алмаштырғыһыҙ икәне асыҡлана: дифференциаль тигеҙләмәләрҙе сығарыу, дәүмәлдәрҙең ҡиммәттәрен классификациялау (мәҫәлән, тауыш интенсивлығы һәм йышлығы), төрлө бәйләнештәрҙең аппроксимацияһы, мәғлүмәт теорияһы, ихтималлыҡ теорияһы һәм башҡалар. Был функция элементар функциялар иҫәбенә инә, ул күрһәткесле функцияға ҡарата кире функция булып тора. Йышыраҡ түбәндәге ысын логарифмдар ҡулланыла:
- нигеҙе буйынса (икеле логарифм),
- нигеҙе буйынса (натураль логарифм) һәм
- ) нигеҙе буйынса (унарлы логарифм).
Ысын логарифм[үҙгәртергә | сығанаҡты үҙгәртеү]
Ысын һандың логарифмы , билдәләмә буйынса, тигеҙләмәһенең сығарылышы булып тора. булған осраҡ әһәмиәтле түгел, сөнки ул саҡта булғанда был тигеҙләмәнең сығарылышы юҡ, ә булғанда теләһә ниндәй һан тигеҙләмәнең сығарылышы була; ике осраҡта ла логарифм билдәһеҙ. Оҡшаш рәүештә нуль йәки тиҫкәре булғанда ла логарифм юҡ икәнен асыҡлайбыҙ; бынан тыш, күрһәткесле функцияһының ҡиммәте һәр саҡ ыңғай, шуға күрә тиҫкәре булған осраҡты төшөрөп ҡалдырырға кәрәк. Ахыр килеп табабыҙ[5]:
|
булғанда ғына ысын логарифмдың мәғәнәһе бар |
Билдәле булыуынса, күрһәткесле функцияһы ( өсөн күрһәтелгән шарттар үтәлгәндә) бар, монотон һәм үҙенең һәр ҡиммәтен бер генә тапҡыр ҡабул итә, шуның менән бергә ҡиммәттәре өлкәһе бөтә ысын ыңғай һандар күмәклеге[6]. Бынан ыңғай һандың ысын логарифмы ҡиммәте һәр саҡ бар һәм берҙән-бер булыуы килеп сыға.
Логарифмдарҙың түбәндәге төрҙәре киң ҡулланыла:
- Натураль логарифмдар: йәки , нигеҙе: Эйлер һаны ();
- Унарлы логарифмдар: йәки , нигеҙе: һаны;
- Икеле логарифмдар: йәки , нигеҙе: .
Улар, мәҫәлән, мәғлүмәт теорияһында, информатикала, дискретлы математиканың күп бүлектәрендә ҡулланылалар.
Үҙсәнлектәре[үҙгәртергә | сығанаҡты үҙгәртеү]
Төп логарифмлы тождество[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифмдың билдәләмәһенән төп логарифмик тождество килеп сыға[7]:
Эҙемтә: ике ысын логарифмдың тигеҙлегенән логарифмланыусы аңлатмаларҙың тигеҙлеге килеп сыға. Ысынлап та, әгәр булһа, ул саҡта , бынан, төп тождествоға ярашлы: .
Берҙең һәм нигеҙенә тигеҙ булған һандың логарифмдары[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифмдың билдәләмәһенән асыҡ күренгән ике тигеҙлек:
Ҡабатландыҡтың, бүлендектең, дәрәжәнең һәм тамырҙың логарифмы[үҙгәртергә | сығанаҡты үҙгәртеү]
Бөтә ҡиммәттәр ҙә ыңғай тип уйлап, формулалар йыйылмаһы килтерәбеҙ[8]:
| Формула | Миҫал | |
|---|---|---|
| Ҡабатландыҡ | ||
| Бүлендек | ||
| Дәрәжә | ||
| Тамыр |
Килтерелгән формулаларҙың, үҙгәреүсәндәрҙең тиҫкәре ҡиммәттәре рөхсәт ителгән осраҡҡа, асыҡ күренеп торған дөйөмләштереүе бар, мәҫәлән:
Ҡабатландыҡтың логарифмы өсөн формулалар ирекле һандағы ҡабатлашыусылар өсөн дөйөмләштерелә:
Юғарыла килтерелгән үҙсәнлектәр, ни өсөн логарифмдарҙы ҡулланыу (калькуляторҙар уйлап табылғанға тиклем) иҫәпләүҙәрҙе ныҡ еңеләйткәнде аңлаталар. Мәҫәлән, логарифмик таблицалар ярҙамында күп урынлы һандарын ҡабатлау [⇨] ошондай алгоритм буйынса башҡарыла:
- таблицаларҙа һандарының логарифмдарын табырға;
- был логарифмдарҙы ҡушырға, (беренсе үҙсәнлеккә ярашлы) ҡабатландығының логарифмы табыла;
- ҡабатландыҡтың логарифмы буйынса таблицаларҙа ҡабатландыҡтың үҙен табырға.
Логарифмдар ярҙамынан башҡа, ҡабатлауға ҡарағанда байтаҡҡа күп хеҙмәт талап иткән бүлеү, шул уҡ алгоритм буйынса башҡарыла, тик логарифмдарҙы ҡушыу алыуға алмаштырыла. Ошоға оҡшаш рәүештә дәрәжәгә күтәреү һәм тамыр алыу ябайлаштырыла.
Логарифмдың нигеҙен алмаштырыу[үҙгәртергә | сығанаҡты үҙгәртеү]
нигеҙе буйынса логарифмын[5] икенсе нигеҙе буйынса логарифмға үҙгәртергә мөмкин:
Эҙемтә ( булғанда) — нигеҙен һәм логарифмланыусы аңлатманы алмаштырып ҡуйыу:
Шундай уҡ алмаштырып ҡуйыу миҫалын унарлы логарифм бүлегендә ҡарағыҙ.
Нигеҙен алмаштырыу формулаһында коэффициенты бер нигеҙҙән икенсе нигеҙгә күсеү модуле тип атала[9].
Тигеҙһеҙлектәр[үҙгәртергә | сығанаҡты үҙгәртеү]
логарифмының ҡиммәте ыңғай шул саҡта һәм тик шул саҡта ғына, әгәр һандары берәмектән бер яҡта ятһалар (йәғни икеһе лә берҙән ҙур, йәки икеһе лә бәләкәй). Әгәр берәмектән төрлө яҡтарҙа ятһалар, ул саҡта логарифм тиҫкәре[10].
Ыңғай һандар өсөн теләһә ниндәй тигеҙһеҙлекте логарифмларға мөмкин. Шуның менән бергә, әгәр логарифмдың нигеҙе берҙән ҙур булһа, тигеҙһеҙлек тамғаһы һаҡлана, ә әгәр логарифмдың нигеҙе берҙән бәләкәй булһа, тигеҙһеҙлек тамғаһы ҡапма-ҡаршыға үҙгәрә[10].
Башҡа тождестволар һәм үҙсәнлектәр[үҙгәртергә | сығанаҡты үҙгәртеү]
Әгәр логарифмдың нигеҙе өсөн аңлатмаға һәм логарифмланыусы аңлатмаға дәрәжәгә күтәреү инһә, ябайлаштырыу өсөн түбәндәге тождествоны ҡулланырға була:
Әгәр һул яҡта логарифмда, юғарыла килтерелгән нигеҙҙе алмаштырыу формулаһы буйынса нигеҙен нигеҙенә алмаштырһаң, был тождество килеп сыға. Эҙемтә:
Тағын бер файҙалы тождество:
Уны иҫбатлау өсөн, уң һәм һул яҡтағы нигеҙе буйынса логарифмдар тап киләләр икәнен иҫкә алабыҙ ( тигеҙҙәр), ә ул саҡта, төп логарифмик тождествонан эҙемтә буйынса, уң һәм һул яҡтары тождестволы тигеҙҙәр. Бынан алдағы тождествоны ирекле нигеҙе буйынса логарифмлап, тағын бер «нигеҙҙәр менән алмашыныу» тождествоһы табабыҙ
Логарифмлы функция[үҙгәртергә | сығанаҡты үҙгәртеү]

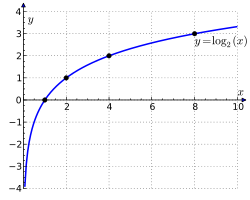
Төп характеристикалары[үҙгәртергә | сығанаҡты үҙгәртеү]
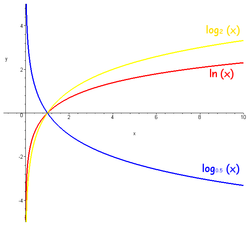
Әгәр логарифмланыусы һанды үҙгәреүсән итеп ҡараһаҡ, беҙ логарифмлы функцияһын алырбыҙ. Уның булғанда мәғәнәһе бар. Ҡиммәттәре өлкәһе: . Был кәкере һыҙыҡ йыш ҡына логарифмика тип атала[11]. #Логарифмдың нигеҙен алмаштырыу формулаһынан күренеүенсә, берҙән ҙурыраҡ төрлө нигеҙле логарифмлы функцияларҙың графиктары, бер-береһенән тик күсәре буйынса масштабтары менән генә айырылалар; берҙән бәләкәйерәк нигеҙҙәр өсөн графиктар уларҙың горизонталь күсәргә ҡарата көҙгөләгесә сағылышы булып торалар.
Билдәләмәнән күренеүенсә, логарифмлы бәйләнеш күрһәткесле функцияһы өсөн кире функция була, шуға күрә уларҙың графиктары беренсе һәм өсөнсө квадранттарҙың биссектрисаһына ҡарата симметрик булалар (һүрәтте ҡарағыҙ). Күрһәткесле функция кеүек үк, логарифмлы функция трансцендентлы функциялар категорияһына ҡарай.
Функция булғанда ҡәтғи үҫә барыусы (артабан графиктарҙы ҡарағыҙ) һәм булғанда ҡәтғи кәмей барыусы була. Теләһә ниндәй логарифмлы функцияның графигы нөктәһе аша үтә. Функция бөтә билдәләнеү өлкәһендә өҙлөкһөҙ һәм сикһеҙ дифференциалланыусы функция.
Ординаталар күсәре () вертикаль асимптотаһы була, сөнки:
- булғанда ;
- булғанда .
Логарифмлы функцияның сығарылмаһы:
- тигеҙ.
Алгебра күҙлегенән ҡарағанда, логарифмлы функция (берҙән бер мөмкин булған) ыңғай ысын һандарҙың мультипликативлы төркөмөнөң һәм бөтә ысын һандарҙың аддитивлы төркөмөнөң изоморфизмын тормошҡа ашыра. Икенсе төрлө әйткәндә, логарифмлы функция функциональ тигеҙләмәнең берҙән-бер (аргументтың бөтә ыңғай ҡиммәттәре өсөн билдәләнгән) өҙлөкһөҙ сығарылышы[12]:
Натураль логарифм[үҙгәртергә | сығанаҡты үҙгәртеү]
Юғарыла килтерелгән сығарылманың дөйөм формулаһынан натураль логарифм өсөн бигерәк тә ябай һөҙөмтә алабыҙ:
Ошо сәбәп менән математик тикшеренеүҙәрҙә башлыса тап натураль логарифмдар ҡулланыла. Улар йыш ҡына дифференциаль тигеҙләмәләрҙе сығарғанда, статистик бәйлелектәрҙе (мәҫәлән, ябай һандарҙың таралыуын) һәм башҡаларҙы тикшергәндә осрай.

-ҙән -ға тиклем интервалда сығарылма өсөн формуланы интеграллап, беҙ табабыҙ:
Икенсе төрлө әйткәндә, натураль логарифм x-тың бирелгән интервалы өсөн гипербола аҫтындағы майҙанға тигеҙ.
Натураль логарифмдан аныҡ булмаған интегралды өлөштәре буйынса интеграллап еңел табырға була:
Математик анализда һәм дифференциаль тигеҙләмәләр теорияһында функцияның логарифмлы сығарылмаһы төшөнсәһе ҙур роль уйнай :
Натураль логарифмды иҫәпләү һәм рәткә тарҡатыу[үҙгәртергә | сығанаҡты үҙгәртеү]
Натураль логарифмды бер эргәһендә Тейлор рәтенә тарҡатайыҡ:
| (Ряд 1) |
Был рәт булғанда йыйылыусан. Атап әйткәндә:
1-се рәт формулаһы, рәт бик яй һәм тик бик тар интервалда йыйылғанлыҡтан, практикала логарифмдарҙы иҫәпләүгә яраҡһыҙ. Әммә унан уңайлыраҡ формуланы сығарыу ҡыйын түгел:
| (Ряд 2) |
Был рәт тиҙерәк йыйыла, бынан тыш, формуланың һул яғы хәҙер теләһә ниндәй ыңғай һандың логарифмын күрһәтә ала. Был алгоритм логарифмдарҙың ҡиммәттәрен реаль һанлы иҫәпләүҙәр өсөн яраҡлы, әммә күп хеҙмәт талап итеү яғынан бик үк яҡшы түгел. Файҙалыраҡ алгоритмдар бар[13].
Унарлы логарифм[үҙгәртергә | сығанаҡты үҙгәртеү]
10 нигеҙе буйынса логарифмдар (тамғаланышы: ) калькуляторҙарҙы уйлап тапҡанға тиклем иҫәпләүҙәр өсөн киң ҡулланылалар. Уларҙың башҡа нигеҙле логарифмдар алдында өҫтөнлөктәре бар: һанының логарифмы -тың бөтөн өлөшөн табыуы еңел[14]:
- Әгәр булһа, ул саҡта һанының бөтөн өлөшөндәге цифрҙар һанынан 1-гә әҙ. Мәҫәлән, аралығында ятыуы аңлашылып тора.
- Әгәр булһа, минус тамғаһы менән алынған, -ҡа бәләкәй яҡтан иң яҡын бөтөн һан, һанының беренсе нуль булмаған цифр алдындағы дөйөм нулдәр һанына тигеҙ (өтөр алдындағы нулде лә индереп). Мәҫәлән, интервалына инә.
Бынан тыш, һанда унарлы өтөрҙө разрядҡа күсергәндә, был һандың унарлы логарифмы ҡиммәте -гә үҙгәрә. Мәҫәлән, . Бынан, унарлы логарифмдарҙы иҫәпләү өсөн -ҙән -ға тиклем диапазондағы һандарҙың логарифмдары таблицаһын төҙөү етә икәне килеп сыға[14].
Натураль логарифм менән бәйләнеш[15]:
Логарифмдарҙы ҡулланыу иҫәпләү техникаһы барлыҡҡа килгәндән һуң бөтөнләй тиерлек туҡтағанлыҡтан, беҙҙең көндәрҙә унарлы логарифм һиҙелерлек дәрәжәлә натураль логарифм тарафынан ҡыҫырыҡлап сығарылды[16]. Ул башлыса тарихи ныҡлы урын алған математик моделдәрҙә һаҡлана — мәҫәлән, логарифмлы шкалалар төҙөгәндә.
Сикке нисбәттәр[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифмдар менән бәйле бер нисә файҙалы сикләмә килтерәйек [17]:
Башҡа үҙсәнлектәре[үҙгәртергә | сығанаҡты үҙгәртеү]
- Гельфонд теоремаһынан, әгәр — алгебраик һандар () булһа, ул саҡта йә рациональ, йәки трансцендент була икәне килеп сыға. Шуның менән бергә, әгәр һандары нисбәте менән бәйле булһалар, шул саҡта ғына логарифм рациональ һәм -ға тигеҙ[18].
- суммаһы (гармоник рәттең өлөшләтә суммаһы) ҙур булғанда үҙен һымаҡ тота, бында — Эйлер — Маскерони даимиһы.
Комплекслы логарифм[үҙгәртергә | сығанаҡты үҙгәртеү]
Билдәләмә һәм үҙсәнлектәре[үҙгәртергә | сығанаҡты үҙгәртеү]
Комплекслы һандар өсөн логарифм, ысын һандар кеүек билдәләнә. Практикала фәҡәт натураль комплекслы логарифм ғына ҡулланыла тиерлек, ул тип тамғалана һәм тигеҙләмәһенең сығарылышы һымаҡ билдәләнә (быныһына эквивалентлы башҡа варианттар түбәндә килтерелә).
Комплекслы һандар яланында был тигеҙләмәнең сығарылышы, ысын һандар осрағынан айырмалы рәүештә, бер ҡиммәтле генә билдәләнмәй. Мәҫәлән, Эйлер тождествоһына ярашлы рәүештә, ; ләкин шулай уҡ . Был шуның менән бәйле, күрһәткесле функция уйҙырма күсәр буйлап ( периоды менән) периодлы функция [19], һәм функция бер үк ҡиммәтте сикһеҙ күп тапҡыр ҡабул итә. Шулай итеп, комплекслы логарифлы функция күп ҡиммәтле була.
Комплекслы нулдең логарифмы юҡ, сөнки комплекслы экспонента нуль ҡиммәтен ҡабул итмәй. Нулдән айырмалы -те күрһәткесле формала күрһәтергә мөмкин:
Ул саҡта [20]:
- формулаһы буйынса табыла.
Бында — ысын логарифм, — ирекле бөтөн һан. Бынан килеп сыға:
|
Комплекслы логарифм теләһә ниндәй өсөн бар, һәм уның ысын өлөшө бер ҡиммәтле билдәләнә, шул уҡ ваҡытта уйланма өлөшөнөң, бөтөн тапҡырға айырылған ҡиммәттәре сикһеҙ күп. |

Формуланан күренеүенсә, уйҙырма ҡиммәттәрҙең береһе һәм тик береһе генә интервалына инә. Был ҡиммәт комплекслы натураль логарифмдың төп ҡиммәте тип атала[11]. Уға ярашлы (хәҙер инде бер ҡиммәтле) функция логарифмдың төп тармағы тип атала һәм тип тамғалана. Ҡайһы берҙә аша логарифмдың төп тармаҡта ятмаған ҡиммәтен дә атайҙар. Әгәр — ысын һан булһа, ул саҡта уның логарифмының төп ҡиммәте ғәҙәттәге ысын логарифм менән тап килә.
Килтерелгән формуланан шулай уҡ, логарифмдың ысын өлөшө аргументтың компоненттары аша түбәндәгесә билдәләнә икәне килеп сыға:
Һүрәттә, компоненттар функцияһы булараҡ ысын өлөшө үҙәк-симметрик һәм координаталар башына тиклемге алыҫлыҡҡа ғына бәйле икәне күрһәтелгән. Ул ысын логарифм графигын вертикаль күсәр тирәләй өйрөлткәндә килеп сыға. Нулгә яҡынайыу менән функция -ҡа ынтыла.
Тиҫкәре һандың логарифмы түбәндәге формула буйынса билдәләнә[20]:
Комплекслы логарифм ҡиммәттәренә миҫалдар[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифмдың () төп ҡиммәтен һәм () ҡайһы бер аргументтар өсөн уның дөйөм аңлатмаһын килтерәйек:
Комплекслы логарифмдарҙы үҙгәрткәндә, уларҙың күп ҡиммәтле икәнен иҫтә тотоп, һаҡ булырға кәрәк, шуға күрә ниндәй ҙә булһа аңлатмаларҙың логарифмдарының тигеҙлегенән был аңлатмаларҙың тигеҙлеге килеп сыҡмай. Хаталы фекерләүгә миҫал:
- — күренеп торған хата.
Һул яҡта логарифмдың төп ҡиммәте тора, ә уңда — аҫта ятҡан тармаҡтағы ҡиммәт () икәнен билдәләп китәйек. Хатаның сәбәбе — үҙсәнлеген һаҡһыҙ ҡулланыу, ул, ғөмүмән алғанда, комплекслы осраҡта логарифм ҡиммәттәренең бөтә сикһеҙ йыйылмаһын күҙ уңында тота, ә төп ҡиммәтен генә түгел.
Комплекслы логарифмлы функция һәм Риман йөҙө[үҙгәртергә | сығанаҡты үҙгәртеү]

Комплекслы анализда комплекслы яҫылыҡтағы күп ҡиммәтле функцияларҙы ҡарау урынына икенсе ҡарар ҡабул ителгән: функцияны бер ҡиммәтле итеп, әммә яҫылыҡта түгел, ә ҡатмарлыраҡ, Риман йөҙө тип аталған төрлөлөктә билдәләнгән тип ҡарарға[21]. Комплекслы логарифмлы функция шулай уҡ ошондай категорияға ҡарай: уның образы (һүрәтте ҡарағыҙ), спираль рәүешендә уралған сикһеҙ һандағы тармаҡтарҙан тора. Был йөҙ өҙлөкһөҙ һәм бер бәйләнешле. Функцияның берҙән-бер нуле (беренсе тәртиптәге) булғанда килеп сыға. Үҙенсәлекле нөктәләре: һәм (сикһеҙ тәртиптәге тармаҡланыу нөктәләре)[22].
Логарифмдың Риман йөҙө, бер бәйләнешле булғанлыҡтан, нөктәһе инмәгән комплекслы яҫылыҡ өсөн универсаль ҡаплаусы булып тора[23].
Аналитик дауамы[үҙгәртергә | сығанаҡты үҙгәртеү]
Комплекслы һандың логарифмы шулай уҡ ысын логарифмдың бөтә комплекслы яҫылыҡҡа аналитик дауамы булараҡ билдәләнергә мөмкин. кәкере һыҙығы берәмектә башлана, нуль аша үтмәй һәм ысын күсәрҙең тиҫкәре өлөшөн киҫмәй икән, ти. Ул саҡта логарифмдың кәкере һыҙығының һуңғы нөктәһендәге төп ҡиммәтен түбәндәге формула буйынса иҫәпләргә мөмкин[22]:
Әгәр — ябай кәкере һыҙыҡ булһа (үҙ-үҙен киҫмәй), ул саҡта унда ятҡан һандар өсөн логарифмлы тождестволарҙы ҡурҡмай ҡулланырға мөмкин, мәҫәлән:
Логарифмлы функцияның төп тармағы өҙлөкһөҙ һәм бөтә комплекслы яҫылыҡта, ысын күсәрҙең тиҫкәре өлөшөнән башҡа, дифференциалланыусы, ысын күсәрҙең тиҫкәре өлөшөндә уйҙырма өлөшө берәмеккә һикереп үҙгәрә. Ләкин был факт төп ҡиммәтенең уйҙырма өлөшөн интервалы менән яһалма сикләү эҙемтәһе булып тора. Функцияның бөтә тармаҡтарын да ҡарағанда, функция бирелмәгән нулдән башҡа бөтә нөктәләҙә лә өҙлөкһөҙлөк үҙсәнлеге үтәлә. Әгәр кәкере һыҙығына ысын күсәрҙең тиҫкәре өлөшөн киҫеп үтергә рөхсәт иткәндә, ул саҡта бындай беренсе киҫелеш һөҙөмтәне төп ҡиммәтенең тармағынан күрше тармаҡҡа күсерә, ә һәр артабанғы киҫелеш логарифмлы функцияның тармаҡтары буйлап оҡшаш шылдырыу тыуҙыра[22] (см. рисунок).
Аналитик дауам формулаларынан, логарифмдың теләһә ниндәй тармағында[19]:
- булыуы килеп сыға.
нөктәһен үҙ эсенә алған теләһә ниндәй әйләнәһе өсөн:
Интеграл ыңғай йүнәлештә алына (сәғәт уғына ҡаршы). Был тождество вычеттар теорияһының нигеҙендә ята.
Комплекслы логарифмдың аналитик дауамын шулай уҡ юғарыла килтерелгән рәттәр ярҙамында билдәләргә мөмкин: комплекслы аргумент осрағына дөйөмләштерелгән ряда 1 йәки ряда 2. Әммә был рәттәрҙең күренешенән, берәмектә рәттең суммаһы нулгә тигеҙ булыуы килеп сыға, йәғни рәт комплекслы логарифмдың күп ҡиммәтле функцияһының төп тармағына ғына ҡарай. Ике рәттең дә йыйылыусанлыҡ радиусы 1-гә тигеҙ.
Кире тригонометрик һәм гиперболик функциялар менән бәйләнеш[үҙгәртергә | сығанаҡты үҙгәртеү]
Комплекслы тригонометрик функциялар экспонента менән (Эйлер формулаһы) бәйләнгән булғанлыҡтан, комплекслы логарифм, экспонентаға кире функция булараҡ, кире тригонометрик функциялар менән бәйле[24][25]:
Гиперболик функцияларҙы комплекслы яҫылыҡта уйланма аргументтың тригонометрик функциялары итеп ҡарарға мөмкин, шуға күрә бында ла логарифм менән бәйләнеш бар[25]:
- — кире гиперболик синус
- — кире гиперболик косинус
- — кире гиперболик тангенс
- — кире гиперболик котангенс
Тарихи очерк[үҙгәртергә | сығанаҡты үҙгәртеү]
Башлап ебәреүселәр[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифмдарҙы ҡулланыуға (Архимедҡа ла билдәле булған[26]), дәрәжәләрҙе ҡабатлағанда уларҙың дәрәжә күрһәткестәре ҡушылыу факты стимул булып тора[27]: . Һиндостандың VIII быуат математигы Вирасена, дәрәжәле бәйләнештәрҙе өйрәнеп, 2, 3, 4 нигеҙҙәре өсөн бөтөн һанлы күрһәткестәр таблицаһын баҫтырып сығара (йәғни, ысынбарлыҡта, логарифмдар таблицаһы)[28].

Урта быуаттар Европаһында хәл иткес аҙым яһала. XVI быуатта ҡатмарлы иҫәпләүҙәргә ихтыяж тиҙ үҫә, һәм ҡыйынлыҡтарҙың һиҙелерлек өлөшө күп урынлы һандарҙы ҡабатлау һәм бүлеү, шулай уҡ тамыр алыу менән бәйле була. Быуат аҙағында бер нисә математиктың бер үк ваҡытта тиерлек башына идея килә: күп хеҙмәт талап иткән ҡабатлауҙы, геометрик һәм арифметик прогрессияларҙы махсус таблицалар ярҙамында сағыштырып, ябай ҡушыу ғәмәле менән алмаштырыу, шуның менән бергә геометрик прогрессия баштағы була[26]. Ул саҡта бүлеү ҙә сағыштырғыһыҙ ябай алыу менән автоматик рәүештә алмаштырыла, шулай уҡ дәрәжәгә күтәреү һәм тамыр алыу ябайлаша.
Беренсе булып был идеяны үҙенең «Arithmetica integra» (1544) китабында Михаэль Штифель баҫтырып сығара, ул, хәйер, үҙенең идеяһын тормошҡа ашырыу өсөн әллә ни көс һалмай[29][30]. Штифелдың төп баһалы хеҙмәте булып дәрәжәнең бөтөн күрһәткестәренән ирекле рациональ күрһәткестәргә күсеү тора[31] (был йүнәлештә беренсе аҙымды XIV быуатта Николай Орем һәм XV быуатта Никола Шюке эшләй).
Джон Непер һәм уның «ғәжәйеп логарифмдар таблицаһы»[үҙгәртергә | сығанаҡты үҙгәртеү]

1614 йылда шотланд математик-һәүәҫкәре Джон Непер латин телендә «Ғәжәйеп логарифмдар таблицаһы һүрәтләмәһе» исемле әҫәрен баҫтырып сығара (лат. Mirifici Logarithmorum Canonis Descriptio). Унда ҡыҫҡаса логарифмдарҙың һәм уларҙың үҙсәнлектәренең тасуирламаһы, шулай уҡ, 1' аҙымы менән, синустарҙың, косинустарҙың һәм тангенстарҙың логарифмдарының 8-урынлы таблицалары бирелә. Непер тәҡдим иткән логарифм термины фәндә нығына. Логарифмдар теорияһын Непер, ул үлгәндән һуң улы Роберт тарафынан 1619 йылда баҫтырып сығарылған, үҙенең икенсе «Построение удивительной таблицы логарифмов» китабында бирә (лат. Mirifici Logarithmorum Canonis Constructio).
Документтарҙан күренеүенсә, логарифмлау техникаһына Непер 1594 йылда уҡ эйә була[32]. Уның асыштарының туранан тура маҡсаты булып, Неперға ҡатмарлы астрологик иҫәпләүҙәрҙе еңелләштереү тора[33]; тап шуның өсөн дә таблицаларға тик тригонометрик функцияларҙың логарифмдары ингән була.
Функция төшөнсәһе ул саҡта булмай әле, һәм Непер логарифмға, тигеҙ һәм логарифмик-яйая барыусы хәрәкәттәрҙе сағыштырып, кинематик билдәләмә бирә; мәҫәлән, синус логарифмына ул ошолай билдәләмә бирә[34]:
Бирелгән синустың логарифмы, һәр саҡ тулы синус геометрик кәмегән кеүек үк тиҙлек менән арифметик үҙә барыусы һан ул.
Хәҙерге тамғалауҙарҙа Неперҙың кинематик моделен дифференциаль тигеҙләмә менән һүрәтләп була[35]:
- ,
бында M — масштаблы ҡабатлашыусы, ул, ҡиммәт кәрәк тиклем тамғалар менән бөтөн һан килеп сыҡһын өсөн индерелгән (унарлы кәсерҙәр ул ваҡытта киң ҡулланылмаған була). Непер M = 10 000 000 итеп алған.
Ҡәтғи әйткәндә, Непер хәҙер логарифм тип аталған функцияны таблицаламаған. Әгәр уның функцияһын тип тамғалаһаң, ул натураль логарифм менән түбәндәгесә бәйләнгән[35]:
Күренеүенсә, , йәғни «тулы синустың» логарифмы (90°-ҡа ярашлы) нуль — Непер үҙенең билдәләмәһе менән ошоға өлгәшергә теләгән дә инде. Шулай уҡ ул, бөтә логарифмдар ҙа ыңғай булыуын теләгән; өсөн был шарттың үтәлеүенә ышаныуы ҡыйын түгел. .
Непер логарифмының төп үҙсәнлеге: әгәр дәүмәлдәр геометрик прогрессия төҙөһә, ул саҡта уларҙың логарифмдары арифметик прогрессия төҙөй. Ләкин өҙлөкһөҙ функция өсөн логарифмлау ҡағиҙәләре хәҙерге логарифм өсөн булған ҡағиҙәләрҙән айырыла, мәҫәлән:
Артабанғы үҫеше[үҙгәртергә | сығанаҡты үҙгәртеү]
Тиҙҙән асыҡланыуынса, алгоритмдағы хата арҡаһында Непер таблицаһындағы бөтә ҡиммәттәрҙә лә алтынсы тамғанан һуң дөрөҫ булмаған цифрҙар киткән[36]. Әммә был иҫәпләүҙәрҙең яңы методикаһына киң билдәлелек алыуға ҡамасауламаған, һәм күп Европа математиктары логарифмик таблицалар төҙөү менән шөғөлләнгән. Кеплер үҙе 1620 йылда баҫтырып сығарған астрономик белешмәгә Неперға һоҡланыулы бағышлама индерә(уйлап табыусының ул ваҡытта инде вафат булғанын белмәйенсә). 1624 йылда Кеплер үҙенең логарифмик таблицалар вариантын баҫтырып сығара (лат. Chilias Logarithmorum ad totidem numeros rotundos)[37]. Логарифмдарҙы ҡулланыу Кеплерға гелиоцентрик астрономияның уңышын нығытыусы Рудольф таблицаларын төҙөү буйынса күп йыллыҡ хеҙмәтен сағыштырмаса тиҙерәк тамамларға мөмкинлек бирә.
Неперҙың китабы баҫылғандан һуң бер нисә йыл үткәс, хәҙерге заман төшөнсәһенә яҡыныраҡ торған логарифмды ҡулланыусы логарифмик таблицалар барлыҡҡа килә. Лондон профессоры Генри Бригс унарлы логарифмдарҙың 14-урынлы таблицаһын төҙөй (1617), шуның менән бергә тригонометрик функциялар өсөн түгел, 1000-гә тиклемге ирекле бөтөн һандар өсөн (7 йылдан һуң Бригс һандар һанын 20000-гә тиклем арттыра). 1619 йылда Лондондың математика уҡытыусыһы Джон Спайделл (ингл. John Speidell) Неперҙың төҙәтелгән һәм тулыландырылған логарифмик таблицаларын киренән баҫтыра, улар ысынында натураль логарифмдар таблицаһы булалар. Спайделл бөтөн һандарға тиклем масштаблауҙы һаҡлаһа ла, уның да 1000-гә тиклемге һандарҙың логарифмдары була (шуның менән бергә берәмектең логарифмы, Бригстыҡы кеүек, нулгә тигеҙ була) [38][39].
Оҙаҡламай логарифмдарҙың математикала урыны иҫәпләүҙәрҙең уңайлылығы менән генә сикләнмәй икәне асыҡлана. 1629 йылда Бельгия математигы Грегуар де Сен-Венсан, гиперболаһы аҫтындағы майҙан логарифмик закон буйынса үҙгәрә икәнен күрһәтә[40]. 1668 йылда немец математигы Николас Меркатор (Кауфман) үҙенең Logarithmotechnia китабында логарифмдың сикһеҙ рәткә тарҡалыуын аса һәм баҫтыып сығара[41]. Күп тарихсыларҙың фекеренсә, логарифмдарҙың барлыҡҡа килеүе күп математик концепцияларға көслө йоғонто яһай, шул иҫәптән:
- Иррациональ һәм трансцендент һандар төшөнсәһенең дөйөм танылыуы һәм формалашыуы[42].
- Күрһәткесле функцияның һәм дөйөм һанлы функция төшөнсәһенең, Эйлер һанының барлыҡҡа килеүе, айырмалы тигеҙләмәләр теорияһының үҫеше[43].
- Сикһеҙ рәттәр менән эш башланыуы[41].
- Төрлө типтағы дифференциаль тигеҙләмәләрҙе сығарыуҙың дөйөм ысулдары.
- Иҫәпләү өсөн теүәл логарифмик таблицалар талап итеүсе һанлы ысулдар теорияһының һиҙелерлек үҫеше.
XIX быуат аҙағына тиклем логарифмдың дөйөм ҡабул ителгән тамғаланышы булмай, a нигеҙе log символынан йә уңда, йә һулда, йә өҫтөндә күрһәтелә. Ахыр сиктә математиктар, нигеҙ өсөн иң уңайлы урын — юлдан түбәнерәк, log символынан һуң тигән фекергә киләләр: . Логарифмдың нығыраҡ ҡулланылған төрҙәренең — унарлы һәм натураль — ҡыҫҡаса тамғаланышы күпкә элегерәк һәм бер юлы бер нисә авторлыҡта килеп сыға һәм шулай уҡ XIX быуат аҙағына тамам нығына[44].
Логарифмлауҙы хәҙерге төшөнсәгә яҡын — дәрәжәгә күтәреүгә кире ғәмәл булараҡ аңлау — беренсе башлап Валлиста (1685) һәм Иоганн Бернуллиҙа (1694) күренә, ә тулыһынса Эйлер тарафынан законлаштырыла[36]. «Введение в анализ бесконечных» (1748) китабында Эйлер күрһәткесле, шулай уҡ логарифмлы функцияларҙың хәҙерге билдәләмәләрен бирә, уларҙың дәрәжәле рәттәргә тарҡалмаһын килтерә, натураль логарифмдың ролен айырым билдәләп китә[45]. Логарифмлы функцияны комплекслы өлкәгә таратыу даны ла Эйлерҙыҡы һанала.
Логарифмды комплекслы өлкәгә киңәйтеү[үҙгәртергә | сығанаҡты үҙгәртеү]
XVII—XVIII быуаттар сигендә Лейбниц һәм Иоганн Бернулли логарифмды комплекслы һандарға киңәйтергә маташалар, ләкин, ул ваҡытта логарифм төшөнсәһенең үҙенең аныҡ билдәләмәһе булмағанлыҡтан, тулы теорияны төҙөй алмайҙар[46]. Был сәбәп буйынса башта Лейбниц һәм Бернулли араһында, ә XVIII быуат уртаһында — Д’Аламбер һәм Эйлер араһында бәхәсләшеү бара. Бернулли һәм Д’Аламбер, тип билдәләргә кәрәк тип иҫәпләйҙәр, шул уҡ ваҡытта Лейбниц, тиҫкәре һандың логарифмы уйҙырма һан икәнен иҫбатлай[46]. Тиҫкәре һәм комплекслы һандарҙың логарифмдарының тулы теорияһы Эйлер тарафынан 1747—1751 йылдарҙа баҫтырып сығарыла һәм хәҙергенән бер ни менән дә айырылмай[47]. Бәхәс дауам итһә лә (Д’Аламбер үҙенең фекерен яҡлай һәм уны үҙенең «Энциклопедия»һында һәм башҡа хеҙмәттәрендә ентекләп аргументлай), Эйлерҙың ҡарашы XVIII быуат аҙағына дөйөм танылыу ала.
XIX быуатта, комплекслы анализ үҫешеү менән, комплекслы логарифмды өйрәнеү яңы асыштарға стимул бирә. Гаусс 1811 йылда, -ҙән интеграл булараҡ билдәләнгән логарифмлы функцияның күп ҡиммәтлелегенең тулы теорияһын эшләй [48]. Риман, был һәм оҡшаш функцияларҙың билдәле факттарына таянып, Риман йөҙҙәренең дөйөм теорияһын төҙөй.
Конформлы сағылыштарҙың теорияһын эшләү, картографияла логарифмдар асышына тиклем үк барлыҡҡа килгән (1550) меркатор проекцияһын комплекслы логарифм һымаҡ тасуирларға мөмкин икәнен күрһәтә[49].
Ҡайһы бер практик ҡулланылыштары[үҙгәртергә | сығанаҡты үҙгәртеү]
Фәндә һәм тәбиғәттә логарифмлы бәйләнештәр[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифмлы функциялар математикала ла, тәбиғәт фәндәрендә лә ныҡ киң таралыу алған. Йыш ҡына логарифмдар үҙенә оҡшашлыҡ булған ерҙә күренәләр, йәғни ниндәйҙер объект эҙмә-эҙ бәләкәйләтелгән һәм ҙурайтылған масштабта яңынан барлыҡҡа килә; түбәндә рекурсивлы алгоритмдар, фракталдар йәки моллюсктар ҡабырсағы кеүек миҫалдарҙы ҡарағыҙ. Логарифмдарҙы төрлө фәндәрҙә ҡулланыуҙың бер нисә миҫалын килтерәйек.
Һандар теорияһы[үҙгәртергә | сығанаҡты үҙгәртеү]
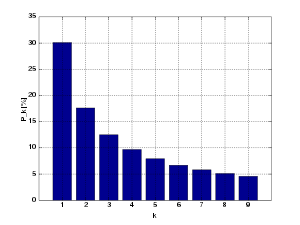
Ябай һандарҙың таралыуы асимптотик ябай закондарға буйһона[50]:
- 1-ҙән -гә тиклем интервалда ябай һандар һаны яҡынса -ға тигеҙ.
- k-сы ябай һан яҡынса -ға тигеҙ.
Тағы ла теүәлерәк баһалауҙар интеграллы логарифмды ҡуллана.
Математик анализ[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифмдар йыш ҡына интегралдарҙы тапҡанда һәм дифференциаль тигеҙләмәләрҙе сығарғанда килеп сығалар. Миҫалдар:
Ихтималлыҡ теорияһы һәм статистика[үҙгәртергә | сығанаҡты үҙгәртеү]
Статистикала һәм ихтималлыҡ теорияһында логарифм бер нисә практик мөһим ихтималлы таралыуға инә. Мәҫәлән, логарифмик таралыу[51] генетикала һәм физикала ҡулланыла. Логнормаль таралыу йыш ҡына өйрәнелеүсе дәүмәл бер нисә бәйләнешһеҙ ыңғай осраҡлы үҙгәреүсәндәрҙең ҡабатландығы булған ситуацияла осрай[52].
Бенфорд законы («беренсе цифр законы») бирелгән мәғәнәле цифрҙың реаль дәүмәлдәрҙе үлсәгәндә килеп сығыу ихтималлығын тасуирлай.
Билдәһеҙ параметрҙы баһалау өсөн максималь ысынға оҡшашлыҡ ысулы һәм уның менән бәйле ысынға оҡшашлыҡ логарифмлы функцияһы киң ҡулланыла[53].
Осраҡлы аҙашып йөрөгәндә флуктуация Хинчин-Колмогоров законы менән һүрәтләнә.
Информатика һәм иҫәпләү математикаһы[үҙгәртергә | сығанаҡты үҙгәртеү]
Информатикала: мәғлүмәт үлсәү берәмеге (бит). Мәҫәлән, компьютерҙа натураль һанын һаҡлау өсөн (компьютер өсөн ғәҙәти икеле форматта) бит кәрәк була.
Информацион энтропия — мәғлүмәт һаны үлсәме.
Тиҙ сортҡа айырыу, Фурьеның тиҙ үҙгәртеүе кеүек, Рекурсивлы алгоритдмарҙың асимптотик ҡатмарлылығын «бүлгеслә һәм хакимлыҡ ит» принцибына нигеҙләнгән баһалау[54] һәм башҡалар
Ғәҙәттә һанлы ҡиммәттәр компьютерҙың йәки махсуслаштырылған процессорҙың хәтерендә күсеп йөрөүсе өтөрлө форматында һаҡланалар. Әгәр, әммә, бирелгән төркөм өсөн ҡушыу һәм алыу һирәк башҡарылһа, ә ҡабатлау, бүлеү, дәрәжәгә күтәреү һәм тамыр алыу — күпкә йышыраҡ, ул саҡта бындай бирелештәрҙе логарифмик форматта һаҡлау мөмкинлеген ҡарау әһәмиәтле. Был осраҡта һан урынына уның модуленең логарифмы һәм тамғаһы һаҡлана, һәм логарифмдың үҙсәнлеге арҡаһында иҫәпләү тиҙлеге һиҙелерлек арта[55]. Логарифмик форматта һаҡлау үҙенең нәтижәлелеген иҫбат иткән бер нисә системала ҡулланыла [56][57].
Фракталдар һәм үлсәнеш[үҙгәртергә | сығанаҡты үҙгәртеү]

Логарифмдар фрактал өсөн Хаусдорф үлсәнешен сағылдырырға ярҙам итәләр[58]. Мәҫәлән, Серпинский өсмөйөшөн ҡарайыҡ, ул тигеҙ яҡлы өсмөйөштән, һәр этапта һыҙыҡлы үлсәме ике тапҡыр кәмей барған, оҡшаш өсмөйөштәрҙе эҙмә-эҙ алып ташлағап килеп сыға (һүрәтте ҡарағыҙ). Һөҙөмтәнең үлсәнеше ошо формула буйынса билдәләнә:
Механика һәм физика[үҙгәртергә | сығанаҡты үҙгәртеү]
Статистик термодинамикала Больцман принцибы — термодинамик системаның буталсыҡлыҡ дәрәжәһен характерлаусы, торошоноң мөһим функцияларының береһе булып тора.
Циолковский формулаһы ракетаның тиҙлеген иҫәпләү өсөн ҡулланыла.
Химия һәм физик химия[үҙгәртергә | сығанаҡты үҙгәртеү]
Нернст тигеҙләмәһе электрохимик тигеҙләмәгә ингән, мәтдәләр активлығы булған системаның окисләнеү-тергеҙелеү потенциалын, шулай уҡ окисланыу-тергеҙелеүсе парҙарҙың стандарт электродлы потенциалдары менән бәйләй.
Логарифм автопротолиз константаһы күрһәткесе (молекуланың үҙенән үҙе ионлашыуы) һәм водородлы күрһәткес (иретмәнең кислоталылығы) кеүек дәүмәлдәрҙең билдәләмәләрендә ҡулланыла.
Музыка теорияһы[үҙгәртергә | сығанаҡты үҙгәртеү]
Октаваны нисә өлөшкә бүлергә тигән мәсьәләне хәл итеү өсөн, өсөн рациональ яҡынайыу табырға кәрәк. Әгәр был һанды өҙлөкһөҙ кәсергә тарҡатһаң, ул саҡта өсөнсө ҡулайлы кәсер (7/12) октаваны 12 ярымтондарға классик бүлеүҙе нигеҙләргә мөмкинлек бирә[59].
Психология һәм физиология[үҙгәртергә | сығанаҡты үҙгәртеү]
Кешенең күп күренештәрҙе үҙләштереүе логарифмик закон ярҙамында яҡшы һүрәтләнә.
Вебер — Фехнер законы — һиҙемдең интенсивлығы стимулдың интенсивлығы логарифмына[60] — тауыштың көсөнә[61], яҡтылыҡ баҙыҡлығына — пропорциональ тигән эмпирик психофизиологик закон.
Фиттс законы: организмдың хәрәкәте һуңыраҡ йәки теүәлерәк үтәлгән һайын, уны үтәүгә шул тиклем ҙурыраҡ коррекция кәрәк һәм шул тиклем оҙағыраҡ был коррекция башҡарыла[62].
Һайлау булғанда ҡарар ҡабул итеүгә ваҡытты en[Hick's law] буйынса баһаларға мөмкин[63].
Биология[үҙгәртергә | сығанаҡты үҙгәртеү]
Күп кенә биологик формалар логарифмик спиралгә — һәр нөктәһендә тейеүсе был нөктәләге радиус-вектор менән бер үк мөйөш яһаған, йәғни әйләнәнең берәмек оҙонлоғона радиус үҫеше даими булған кәкере һыҙыҡҡа — яҡшы тап киләләр[64] :
-
Наутилус ҡабырсағы -
Көнбағышта орлоҡтарҙың урынлашыуы
Төрлөһөнән[үҙгәртергә | сығанаҡты үҙгәртеү]
Олимпия системаһында уйындар әйләнеше һаны, ярышта ҡатнашыусылар һанының икеле логарифмына тигеҙ[65].
Логарифмик шкала[үҙгәртергә | сығанаҡты үҙгәртеү]

Унарлы логарифмдарҙың Тигеҙһеҙ шкалаһы фәндең күп өлкәләрендә ҡулланыла. Иҫәпләүҙәрҙе тәьмин итеү өсөн ул логарифмик линейкаға төшөрөлә. Башҡа миҫалдар:
- Акустика — тауыш баҫымы кимәле һәм тауыш көсөргәнешлелеге (децибелдар)[66].
- Радиотехникала һәм Электроэлемтәлә [[сигнал/тауыш] нисбәте][67].
- Астрономия — йондоҙ яҡтылығы шкалаһы[68].
- Химия — водородлы иондарҙың активлығы (pH)[69].
- Сейсмология — Рихтер шкалаһы[70].
- Оптик тығыҙлыҡ — үтә күренеүсән объекттарҙың яҡтылыҡты йотоу йәки үтә күренмәгән объекттарҙың яҡтылыҡты сағылдырыу үлсәме [71].
- Идара итеү теорияһы — логарифмик амплитуда-фаза йышлыҡ характеристикаһы[72].
Логарифмик шкала бигерәк тә үлсәнеүсе дәүмәлдең кимәлдәре геометрик прогрессия төҙөгән осраҡта уңайлы, сөнки ул саҡта уларҙың логарифмдары даими аҙым менән тарала. Мәҫәлән, классик октаваның 12 ярымтоны (яҡынса), знаменателе -гә тигеҙ булған, шундай прогрессияны төҙөй[59]. Оҡшаш рәүештә, Рихтер шкалаһының һәр кимәле алдағы кимәлгә ҡарағанда 10 тапҡыр күберәк энергияға ярашлы. Хатта геометрик прогрессия булмағанда ла логарифмик шкаланың үлсәнеүсе дәүмәлдең киң диапазондағы ҡиммәттәрен йыйнаҡ күрһәтеү өсөн файҙаһы тейергә мөмкин.
Логарифмик шкала шулай уҡ дәрәжәле бәйләнештәрҙең дәрәжә күрһәткесен һәм экспонента күрһәткесендә коэффициентты баһалау өсөн киң ҡулланыла. Шуның менән бергә бер йәки ике күсәр буйынса логарифмик масштабта төҙөлгән график, тикшереү өсөн ябайыраҡ булған тура һыҙыҡ күренешен ала.

Өҫкө рәт — 1) икеһе лә һыҙыҡлы; 2) логарифмик (x) һәм һыҙыҡлы (y);
Аҫҡы рәт — 1) һыҙыҡлы (x) һәм логарифмик (y); 2) икеһе лә логарифмик.
Логарифмик таблицалар[үҙгәртергә | сығанаҡты үҙгәртеү]

Логарифмдың үҙсәнлегенән, күп урынлы һандарҙы күп хеҙмәт талап иткән ҡабатлау урынына, (таблицалар буйынса) уларҙың логарифмдарын табыу һәм ҡушыу етә, ә аҙаҡ шул уҡ таблицалар буйынса («Антилогарифмдар бүлеге») потенцирләүҙе башҡарырға, йәғни логарифмы буйынса һөҙөмтәнең ҡиммәтен табырға кәрәк. Бүлеүҙе башҡарыу, логарифмдар алыныуы менән генә айырыла.
Логарифмдарҙың беренсе таблицаларын Джон Непер (1614) баҫтырып сығара, һәм уларға тик тригонометрик функцияларҙың логарифмдары ғына ингән була, шуның менән бергә хаталы. Уға бәйһеҙ рәүештә үҙенең таблицаларын Йост Бюрги, Кеплерҙың дуҫы (1620) баҫтырып сығара. 1617 йылда Оксфордтың математика профессоры Генри Бригс 1-ҙән 1000-гә тиклем һандарҙың 8 (һуңғараҡ — 14) тамға менән унарлы логарифмдары ингән таблицаларын баҫтырып сығара. Ләкин Бригстың таблицаларында ла хаталар табылған. Георг Вега таблицалары нигеҙендә беренсе хатаһыҙ таблица (1783) тик 1857 йылда ғына Берлинда барлыҡҡа килә (Бремикер таблицалары, Carl Bremiker)[73].
Рәсәйҙә беренсе логарифмдар таблицаһы 1703 йылда Л. Ф. Магницкий ҡатнашлығында баҫылып сыға[74]. СССР-ҙа логарифмдар таблицаларының бер нисә йыйынтығы баҫтырып сығарыла[75]:
- Брадис В. М. Дүрт урынлы математик таблицалар. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Ете урынлы логарифмдар таблицалары, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
- Бремикер К. Логарифм-тригонометрик таблицалар. М.: Наука, 1962. 664 с. Классические шестизначные таблицы, удобные для расчётов с тригонометрическими функциями.
- Тригонометрик дәүмәлдәрҙең натураль ҡиммәттәренең, уларҙың логарифмдарының һәм һандар логарифмдарының биш урынлы таблицалары, 6-е издание, М.: Наука, 1972.
- Натураль логарифмдар таблицалары, 2-е издание, в 2 томах, М.: Наука, 1971.
- Комплекслы һандарҙың логарифмдарының ун ҡиммәтле таблицалары. М., 1952.
Логарифмик линейка[үҙгәртергә | сығанаҡты үҙгәртеү]
1620-cе йылдарҙа Эдмунд Уингейт һәм Уильям Отред беренсе логарифмик линейканы уйлап табалар, улар кеҫә калькуляторҙары барлыҡҡа килгәнсе инженерҙың алмаштығыһыҙ иҫәпләү ҡоралы булып хеҙмәт итәләр[76]. Был компактлы инструмент ярҙамында тиҙ генә бөтә алгебраик ғәмәлдәрҙе башҡарып була, шул иҫәптән тригонометрик функциялар ҡатнашлығында[77]. Иҫәпләү аныҡлығы — яҡынса 3 мәғәнәле цифр.

Вариациялар һәм дөйөмләштереүҙәр[үҙгәртергә | сығанаҡты үҙгәртеү]
Логарифм тигеҙләмәһенең сығарылышы булараҡ ысын һәм комплекслы һандар өсөн генә билдәләнмәй.
- Логарифмлы функцияны кватерниондар өсөн индерергә була (ҡарағыҙ. Кватернион#Кватернионлы үҙгәреүсән функциялары). Ләкин логарифмдың күпселек алгебраик үҙсәнлектәре был осраҡта юғала[78] — мәҫәлән, ҡабатландыҡтың логарифмы логарифмдар суммаһына тигеҙ түгел, һәм был бындай дөйөмләштереүҙең практик әһәмиәтен кәметә.
- Әгәр — Абелевтың сикле мультипликативлы төркөмөнөң элементтары булһалар, ул саҡта логарифм был мәғәнәлә (әгәр ул булһа) дискретлы тип атала. Йышыраҡ ул ниндәйҙер модуль буйынса вычеттар ҡулсаһының сикле төркөмө өсөн ҡарала, ул был модуль буйынса индекс тип атала[79] һәм криптографияла мөһим роль уйнай. Цикллы төркөмдәрҙә, әгәр логарифмдың нигеҙе был төркөмдөң алынма тамыры булһа, логарифм бар.
- Матрицалы логарифм[en]: логарифмдарҙы шулай уҡ матрицалар өсөн билдәләргә була[80].
- Бик ҙур һандар менән эшләү өсөн, дәрәжәгә күтәреү менән түгел, ә юғарыраҡ тәртиптәге ғәмәл — тетрация менән бәйле суперлогарифм төшөнсәһе индерелә.
Шулай уҡ ҡарағыҙ[үҙгәртергә | сығанаҡты үҙгәртеү]
- Антилогарифм
- Логарифмлы вычет
- Йыйылыусанлыҡтың логарифмлы билдәһе
- Логарифмик ҡағыҙ
- Полилогарифм
- Дәүмәлдең тәртибе
- Простаферетик функция
- Логарифмик функцияларҙан интегралдар теҙеме
Иҫкәрмәләр[үҙгәртергә | сығанаҡты үҙгәртеү]
- ↑ Краткий словарь иностранных слов. М.: Русский язык, 1984.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 186
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 184—186
- ↑ Швецов К. И., Бевз Г. П. Справочник по элементарной математике. Арифметика, алгебра. Киев: Наукова Думка, 1966. § 40. Исторические сведения о логарифмах и логарифмической линейке.
- ↑ 5,0 5,1 Корн Г., Корн Т. Справочник по математике, 1973, с. 34
- ↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 229.
- ↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187
- ↑ Элементарная математика, 1976, с. 93f
- ↑ 10,0 10,1 Элементарная математика, 1976, с. 89
- ↑ 11,0 11,1 Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 159-160
- ↑ Sasaki T., Kanada Y. Practically fast multiple-precision evaluation of log(x) (инг.) // Journal of Information Processing. — 1982. — В. 4. — Т. 5. — С. 247–250.
- ↑ 14,0 14,1 Элементарная математика, 1976, с. 94—100
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 164
- ↑ Baker, Alan (1975), «Transcendental number theory», Cambridge University Press, ISBN 978-0-521-20461-3, p. 10.
- ↑ 19,0 19,1 Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 520-522
- ↑ 20,0 20,1 Корн Г., Корн Т. Справочник по математике, 1973, с. 623
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 92—94
- ↑ 22,0 22,1 22,2 Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 45—46, 99-100
- ↑ Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 522-526
- ↑ 25,0 25,1 Корн Г., Корн Т. Справочник по математике, 1973, с. 624
- ↑ 26,0 26,1 Успенский Я. В. Очерк истории логарифмов, 1923, с. 9
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 206
- ↑ Gupta, R. C. (2000), "History of Mathematics in India", in Hoiberg, Dale & Ramchandani, «Students' Britannica India: Select essays», New Delhi: Popular Prakashan, с. 329
- ↑ История математики, том II, 1970, с. 54—55
- ↑ Vivian Shaw Groza, Susanne M. Shelley (1972), «Precalculus mathematics», New York: Holt, Rinehart, Winston, с. 182, ISBN 978-0-03-077670-0, <https://books.google.com/?id=yM_lSq1eJv8C&pg=PA182&dq=%22arithmetica+integra%22+logarithm&q=stifel>
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 210
- ↑ Успенский Я. В. Очерк истории логарифмов, 1923, с. 13
- ↑ История математики, том II, 1970, с. 56
- ↑ Хрестоматия по истории математики. Математический анализ. Теория вероятностей / Под ред. А. П. Юшкевича. — М.: Просвещение, 1977. — С. 40. — 224 с.
- ↑ 35,0 35,1 История математики, том II, 1970, с. 59
- ↑ 36,0 36,1 История математики, том II, 1970, с. 61
- ↑ Успенский Я. В. Очерк истории логарифмов, 1923, с. 39
- ↑ История математики, том II, 1970, с. 63
- ↑ Charles Hutton. Mathematical Tables. London, 1811, p. 30.
- ↑ История математики, том II, 1970, с. 133
- ↑ 41,0 41,1 Успенский Я. В. Очерк истории логарифмов, 1923, с. 52
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 51, 286, 352
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 213, 217
- ↑ Cajori. Florian. A History of Mathematics, 5th ed. — AMS Bookstore. — P. 152. — ISBN 0821821024.
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 25.
- ↑ 46,0 46,1 История математики, том III, 1972, с. 325—328
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230-231.
- ↑ Математика XIX века. Том II: Геометрия. Теория аналитических функций, 1981, с. 122—123
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. II. Геометрия. — С. 159—161. — 416 с.
- ↑ Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
- ↑ Weisstein, Eric W. Log-Series Distribution (ингл.). MathWorld. Дата обращения: 26 апрель 2012.
- ↑ Логарифмически нормальное распределение // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Максимального правдоподобия метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Harel, David; Feldman, Yishai A. Algorithmics: the spirit of computing. — New York: Addison-Wesley, 2004. — P. 143. — ISBN 978-0-321-11784-7.
- ↑ N. G. Kingsburg, P. J. W. Rayner (Jan. 28, 1971). «Digital filtering using logarithmic arithmetic». Electronics Letters 7: 55.
- ↑ R. C. Ismail and J. N. Coleman (July 2011). «ROM-less LNS». 2011 20th IEEE Symposium on Computer Arithmetic (ARITH): 43–51. DOI:10.1109/ARITH.2011.15.
- ↑ Haohuan Fu, Oskar Mencer, Wayne Luk (June 2010). «Comparing Floating-point and Logarithmic Number Representations for Reconfigurable Acceleration». IEEE Conference on Field Programmable Technology: 337. DOI:10.1109/FPT.2006.270342.
- ↑ Иванов М. Г. Размер и размерность // «Потенциал», август 2006.
- ↑ 59,0 59,1 Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. М.: Физматгиз, 1963. 20 с. Серия «Популярные лекции по математике», выпуск 37.
- ↑ Головин С. Ю. ЗАКОН ВЕБЕРА-ФЕХНЕРА // Словарь практического психолога. Дата обращения: 17 апрель 2012. Архивировано 28 май 2012 года.
- ↑ Ирина Алдошина. Основы психоакустики // Звукорежиссёр. — 1999. — В. 6.
- ↑ Закон Фиттса // Психологическая энциклопедия. Дата обращения: 17 апрель 2012. Архивировано 28 май 2012 года. 2015 йыл 2 июль архивланған.
- ↑ Welford, A. T. Fundamentals of skill. — London: Methuen, 1968. — P. 61. — ISBN 978-0-416-03000-6.
- ↑ Логарифмическая спираль // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров. — М.: Советская энциклопедия, 1988. — С. 328. — 847 с. — ISBN 5-85270-278-1.
- ↑ Харин А. А. Организация и проведение соревнований. Методическое пособие. — Ижевск: УдГУ, 2011. — С. 27.
- ↑ Децибел // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Учебно-методический комплекс: Методы и средства обработки сигналов. Дата обращения: 28 апрель 2012. Архивировано 19 февраль 2012 года. 2012 йыл 19 март архивланған.
- ↑ Звёздная величина // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Бейтс Р. Определение рН. Теория и практика. — 2 изд. — Л.: Химия, 1972.
- ↑ Рихтера шкала. География. Современная иллюстрированная энциклопедия. — М.: Росмэн. Под редакцией проф. А. П. Горкина. 2006. Архивировано 23 август 2011 года.
- ↑ Ҡалып:Книга:ФКТЭ
- ↑ Понятие частотных характеристик. Дата обращения: 28 апрель 2012. Архивировано 28 май 2012 года.
- ↑ История математики, том II, 1970, с. 62
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е. — М.: КомКнига, 2005. — С. 66. — 296 с. — ISBN 5-484-00123-4.
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
- ↑ История математики, том II, 1970, с. 65—66
- ↑ Березин С. И. Счётная логарифмическая линейка. — М.: Машиностроение, 1968.
- ↑ David Eberly. Quaternion algebra and calculus (ингл.) (2 март 1999). Дата обращения: 12 апрель 2012. Архивировано 28 май 2012 года.
- ↑ Виноградов И. М. Основы теории чисел. — М.-Л.: ГИТТЛ, 1952. — С. 97. — 180 с.
- ↑ Гантмахер Ф. Р. Теория матриц. — М.: Наука, 1967. — 576 с.
Әҙәбиәт[үҙгәртергә | сығанаҡты үҙгәртеү]
- Теория логарифмов
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
- Шахмейстер А. Х. Логарифмы. Пособие для школьников, абитуриентов и преподавателей. — изд. 5-е. — СПб.: МЦНМО, 2016. — 288 с. — ISBN 978-5-4439-0648-5.
- История логарифмов
- Абельсон И. Б. Рождение логарифмов. — М.—Л.: Гостехиздат, 1948. — 231 с.
- Гиршвальд Л. Я. История открытия логарифмов. — Харьков: Изд-во Харьковского университета, 1952. — 33 с.
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Геометрия. Теория аналитических функций. — М.: Наука, 1981. — Т. II.
- Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.




































![{\displaystyle \log _{a}{\sqrt[{p}]{x}}={\frac {\log _{a}(x)}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ece430566cd091b2e5ceaf74f52fee70f36b9f0f)














![{\displaystyle \log _{a^{k}}b={\frac {1}{k}}\log _{a}b;\quad \log _{\sqrt[{n}]{a}}b=n\log _{a}b;\quad \log _{a^{k}}b^{k}=\log _{a}b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e316e08f1d78cbd9b344d7919c72f89149e41f5d)





























![{\displaystyle [\lg x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95dba0944686ae335cc4855187bf6270ee6c856d)














![{\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7901ca277e9fe1a5be535f262d7d4a84fc51a3f)





















![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)



















































![{\displaystyle {\sqrt[{12}]{2}}\approx 1{,}059}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4ddcc20b1bbf71fb3749894165cd274910b7aaa)



