Төҙөлөш механикаһы
Төҙөлөш механикаһы — конструкцияның ныҡлығы, ҡатылығы, тотороҡлоғо тураһында фәндәр төркөмө. Фәнде Галилео Галилей, Роберт Гук (1635-1705), Леонард Эйлер, Дмитрий Иванович Журавский, Томас Юнг (1773-1829), Барре де Сен-Венан, Виктор Львович Кирпичёв, Степан Прокофьевич Тимошенко, Исаак Моисеевич Рабинович, Якоб Бернулли (1654-1705) һәм башҡалар өйрәнделәр.

Классик бүлектәре:
- Материалдар ҡаршылығы
- Һығылмалыҡ теорияһы
- Йомшаҡлыҡ теорияһы
- Ҡоролмалар теорияһы ( статика, динамика , ҡоролмалар тотороҡлоғо)[1]
Тарих[үҙгәртергә | сығанаҡты үҙгәртеү]
1822 йылда француз математигы һәм механигы Огюстен Луи Коши (1789-1857) «көсөргәнеш» һәм деформация терминдарҙы фән әҙәбиәткә индерҙе.
1826 йылда француз инженер Луи Мари Анри Навье (1785-1836) һығылмалылыҡ модуле индерҙе.
Материалдар ҡаршылығы[үҙгәртергә | сығанаҡты үҙгәртеү]
Материалдар ҡаршылығы - механика фәненең бер өлөшө. Материалдын ныҡлығы, ҡатылығы, тотороҡлоғон өйрәнә. Кендектен киселешендә эске көсөргәнештәр. Эске көсөргәнеш табыу ысулы немец инженерҙар А. Риттер, Д. Шведлер(1851) менән тәкдим ителде.
Закондар[үҙгәртергә | сығанаҡты үҙгәртеү]
ҡайҙа — материалға һалынған көс, -майҙан
ҡайҙа материалдын физик константаһы (Юнг модуле), -сағыштырма озоноуы.
ҡайҙа материалдын физик константаһы (Юнг модуле), -сағыштырма озоноуы. ҡорос өсөн Юнг модуле , Мпа.
ҡайҙа материал деформацияһы, -материал оҙонлоғо.
Бөгөлөү ваҡытта көсөргәнеш.
Һаҡлам коэффициенты[үҙгәртергә | сығанаҡты үҙгәртеү]
ҡайҙа — предел дәүмәле (көс, көсөргәнеш һәм башҡа);
— дәүмәлден расчет күрһәткесе
Ҡорлманын эшләү көсө:
,
где — Һаҡлам коэффициенты минимумы.
Иң түбән Һаҡлам коэффициенттар аэрокосмос сәнәғәтендә ҡулланыла (ракеталарҙын массаны түбән эщләү өсөн). AҠШ-та:
- (margin of safety);
- (reverse factor).
Тартылыуға ныҡлыҡ[үҙгәртергә | сығанаҡты үҙгәртеү]
| Материал | Ағыу сиге (MPa) |
Ныҡлыҡ сиге (MPa) |
Тығыҙлыҡ (g/cm³) |
|---|---|---|---|
| ASTM A36 Ҡорос Ҡоростары | 250 | 400 | 7.8 |
| Йомшаҡ ҡорос 1090 | 248 | 841 | 7.58 |
| Кеше тиреһе | 15 | 20 | 2.2 |
| Micro-Melt® 10 Ҡаты йығаз ҡоросы (AISI A11) [2] | 5171 | 5205 | 7.45 |
| 2800 Мартен ҡоросы [3] | 2617 | 2693 | 8.00 |
| AerMet 340[4] | 2160 | 2430 | 7.86 |
| Sandvik Sanicro 36Mo кабеле [5] | 1758 | 2070 | 8.00 |
| AISI 4130 Ҡоросо, 855 °C (1570 °F) температурала һыуҙы биргәндә, 480 °C (900 °F) temper[6] | 951 | 1110 | 7.85 |
| Titanium 11 (Ti-6Al-2Sn-1.5Zr-1Mo-0.35Bi-0.1Si), Титан [7] | 940 | 1040 | 4.50 |
| Ҡорос, API 5L X65[8] | 448 | 531 | 7.8 |
| Ҡорос, high strength alloy ASTM A514 | 690 | 760 | 7.8 |
| Юғары тығыҙлык менән полипропилен (HDPE) | 26-33 | 37 | 0.95 |
| Полипролен | 12-43 | 19.7-80 | 0.91 |
| тутыҡмай торған Ҡорос оAISI 302 - Cold-rolled | 520 | 860 | 8.19 |
| Суйын 4.5% C, ASTM A-48 | 130 | 200 | |
| "Liquidmetal" сплавы Ҡалып:Citation needed | 1723 | 550-1600 | 6.1 |
| Берилий [9] 99.9% Be | 345 | 448 | 1.84 |
| Аллюминий [10] 2014-T6 | 414 | 483 | 2.8 |
| Polyester resin (unreinforced)[11] | 55 | ||
| Polyester and Chopped Strand Mat Laminate 30% E-glass[11] | 100 | ||
| S-Glass Epoxy composite[12] | 2358 | ||
| Aluminium alloy 6061-T6 | 241 | 300 | 2.7 |
| Copper 99.9% Cu | 70 | 220 | 8.92 |
| Cupronickel 10% Ni, 1.6% Fe, 1% Mn, balance Cu | 130 | 350 | 8.94 |
| Brass | 200 + | 550 | |
| Tungsten | 1510 | 19.25 | |
| Glass | 33[13] | 2.53 | |
| E-Glass | N/A | 1500 for laminates, 3450 for fibers alone |
2.57 |
| S-Glass | N/A | 4710 | 2.48 |
| Basalt fiber | N/A | 4840 | 2.7 |
| мрамор | N/A | 15 | |
| Бетон | N/A | 3 | 2.7 |
| Carbon fiber | N/A | 1600 for Laminate, 4137 for fiber alone |
1.75 |
| Carbon fiber (Toray T1000G)[14] | 6370 fibre alone | 1.80 | |
| Кеше сәсе | 380 | ||
| Bamboo | 350-500 | 0.4 | |
| Spider silk (See note below) | 1000 | 1.3 | |
| Darwin's bark spider silk[15] | 1652 | ||
| Silkworm silk | 500 | 1.3 | |
| Aramid (Kevlar or Twaron) | 3620 | 3757 | 1.44 |
| UHMWPE[16] | 24 | 52 | 0.97 |
| UHMWPE fibers[17][18] (Dyneema or Spectra) | 2300-3500 | 0.97 | |
| Vectran | 2850-3340 | ||
| Polybenzoxazole (Zylon)[19] | 2700 | 1.56 | |
| Pine wood (parallel to grain) | 40 | ||
| Bone (limb) | 104-121 | 130 | 1.6 |
| Нейлон, type 6/6 | 45 | 75 | 1.15 |
| Epoxy adhesive | - | 12 - 30[20] | - |
| Rubber | - | 15 | |
| Boron | N/A | 3100 | 2.46 |
| Силикон, monocrystalline (m-Si) | N/A | 7000 | 2.33 |
| Silicon carbide (SiC) | N/A | 3440 | |
| Ultra-pure silica glass fiber-optic strands[21] | 4100 | ||
| Sapphire (Al2O3) | 400 at 25*C, 275 at 500*C, 345 at 1000*C | 1900 | 3.9-4.1 |
| Boron Nitride Nanotube | N/A | 33000 | ? |
| Diamond | 1600 | 2800 | 3.5 |
| Graphene | N/A | 130000[22] | 1.0 |
| First carbon nanotube ropes | ? | 3600 | 1.3 |
| Colossal carbon tube | N/A | 7000 | 0.116 |
| Carbon nanotube (see note below) | N/A | 11000-63000 | 0.037-1.34 |
| Carbon nanotube composites | N/A | 1200[23] | N/A |
| Iron (pure mono-crystal) | 3 | 7.874 |
Принциптар[үҙгәртергә | сығанаҡты үҙгәртеү]
Д’Аламбе́р при́нцибы — төҙөлөш механикаһында, материалдар ҡаршылығында, Ҡоролмалар теорияһында динамиканың нигеҙ принцибы. Ошо приницп буйынса актив көстәрғә инерция көстәре ҡушып тигеҙләшкән көстәр системаһы тыуа. Уның тураһында Д’Аламбер Жан Лерон «Динамика» (1743) китапта яҙҙы. Ошо принцип буйынса, системаның һәр i-се нөктә өсөн дөрөҫ: , ҡайҙа — системаға бирелғән актив көсө, — нөктәғә һалынған элемтәнең реакцияһы, —масса һәм ҡабатландығы(инерция көсө), тиҙлелегенә ҡаршы йүнәлешле ().
Ысынбарлыҡта был Ньютондын икенсе законы () үтәүе. Ҡушылыусы Д’Аламбер инерция көсө тип атала.
Азатлыҡ дәрәжәһе(Механикала) — есемдең арауыҡта урын алмаштырыуы ваҡытта ирекһеҙ координаталар дөйөмлөғө. Был механиканың нигеҙ төшөнсәһе.
Ысынбарлыҡта азатлыҡ дәрәжәһе— есемде арауыҡта табыу өсөн минималь һаны (координата).
Мәҫәлән математика маятниғының арауыҡта азатлыҡ дәрәжәһе — 2, бер яҫылыҡта әйләнғән маятниҡтын — 1 (сөнки уның координатаны мөйөш аша табырға мөмкин — 1 һан).
Бәйләнғән механик системаһына ҡарағанда, уның азатлыҡ дәрәжәһе һаны, системаның нөктәләрҙен бөтә декарт координаталарҙан түбән:
ҡайҙа n — азатлыҡ дәрәжәһе, N — системаның материаль нөктәләр һаны, nlink — бәйләнғән элемтәләр һаны (артыҡ элемтәләрһеҙ).
Төҙөлөш механикаһында яҫы системаһының азатлыҡ дәрәжәһен табыу
Ҡайҙа:
-азатлыҡ дәрәжәһе -дисктар һаны, -ябай шарнирҙар һаны, -таяныс элемтәләр һаны.
Ләкин ошо формула аңлау өсөн ҡыйын. Сөнки рамала күп контурҙар булғас, элементтарҙы дисктарға бүлеү ҡыйын[24]/.
Ошо ҡыйынлыҡты үтеү өсөн А. А. Кутонова, В. И. Уварова, Б. А. Тухфатуллин менән ошо формула тәкдим ителде[24]/:
Ҡайҙа:
-азатлыҡ дәрәжәһе - быуындар һаны, -ябай шарнирҙар һаны,
-таяныс элемтәләр һаны.
Таяныстар төрҙәре
- күсемле шарнир таянысы
- күсемһеҙ шарнир таянысы
- ярыҡ таянысы
Ҡоролманың расчёт схемаһы[үҙгәртергә | сығанаҡты үҙгәртеү]
Ҡоролманың расчёт схемаһы — төҙөлөш механикаһында расчёт өсөн алынған ябайлаштырылған ҡоролма һүрәте. Расчёт схемаларҙын төрлө төрҙәре бар. Расчёт схема үткерһерәк булға – расчёт ҡыйыныраҡ була.
Расчёт схемаларҙын төрҙәре:
- Арауыҡта эшләү буйынса: бер, ике, өс үлсәүле
- Билдәһеҙ элементтар буйынса – дискрет, дискрет-континуаль һәм континуаль.
- Расчёт схемаларҙа ҡулланылған конструкциялар буйынса – кендек, пластина, тышлыҡ, ауыр-ҙур
- Инерция көстәрҙе иҫәпләү буйынса – статик һәм динамика
Расчет схеманың элементтары:
- кендектәр
- пластиналар
- тышлыҡтар
- массивтар
- элемтәләр
Кендектәр балкалар, стойкалар, аркалар һәм ошо элементтарҙан торған конструкциялар (ферма, рамалар, сетка тышлыҡтар), яҫылыҡ конструкцияларҙы яҡынса расчетлау өсөн (мәҫәлән йорттарҙын стеналары) ҡулланыла. Өсмөйөш һәм дүртмөйөш пластиналар яҫылыҡ конструкцияларҙы расчетлау өсөн ҡулланыла (стеналар, түшәмдәр). Оболочкалар – арауыҡ конструкцияларҙын (куполдар, сводтар) расчёт схемаһы булып тора. Массивтар расчет схемаларҙа ҡыҫылған нигеҙдә ятҡан деформацияланмаған таяныстар һымаҡ ҡулланыла. Элемтәләр элементтарҙы берләштерә. [25]
Күп ҡатлы йорттарҙын расчёт схемалары[үҙгәртергә | сығанаҡты үҙгәртеү]
Күп ҡатлы йорттар арауыҡ системалар. [26] [27] Бер үлсәүле расчет схема буйынса йорт консоль йоҡа кендек ярыҡта торған һымаҡ ҡүрһәтелә.
Дискрет расчет схемаларҙа билдәһеҙ көстәр йәки күсерелештәр алгебра тигеҙләмәләр төҙөү менән табыла. Дискрет-континуаль расчёт схемаларҙа билдәһеҙ көстәр функциялар аша табыла. Билдәһеҙ функциялар дифференциаль тигеҙләмәләр сисеү менән табыла. Ҡушма кендектәр теорияла кендектәр буйылы һәм бөгөлөү көстәрҙән деформациялана. Ләкин күп ҡатлы йорттарҙын вертикаль диафрагмалары шыуышыуҙан юҡҡа сыға. А. Р. Ржаницын һәм В. З. Власов шыуышыу, буйылы һәм бөгөлөү көстәр бергә эшләүҙе өйрәнделәр [28] В. И. Лишак, [26] [29] .Б. П. Вольфсон [30] Шулай уҡ ошо өлкәһендә эшләнеләр.
Аркалар[үҙгәртергә | сығанаҡты үҙгәртеү]
Аркалар расчет нигеҙендә кәкре кендек расчеты ята. Шыуышыу көсөргәнеше яҡынса тура таяҡ өсөн формула аша табалар [31]:
- ,
ҡайҙа
- — арҡыры көс
- — нейтраль күсәрҙән z аралыҡта торған нөктә өсөн статик моменты
- — киҫелештен инерция моменты
- — киҫелештен киңлеғе
Ныҡлыҡ булаясаҡ [31]:
- .
Кәкре кендектә булған нормаль көсөргәнеш:[31]:
- ,
ҡайҙа
- — нормаль көсө
- — киҫелеш майҙаны

Бөгөлгән момент (тура таяҡта һымаҡ) [31]:
- ,
ҡайҙа
- — нейтраль күсәрҙән z көсөргәнеш табылған нөктәһә тиклем алыҫлыҡ
- — нөктәлә кәкре радиусы
- —моменттан эргәләш киҫелештәр араһында мөйөш үҙгәреү һаны
- —киҫелештәр араһында башланғыс мөйөш
- — Юнг модуле.
Шулай булғас тура таяҡ менән сағыштырғанда кәкре кендектә (аркала) нормаль напряжениялар гипербола закон буйнса табыла. Ошонан мөғим сығармалар:
- кәкре кендек бөгөлөүҙә нейтраль күсәр асыл аша үтмәй
- тышкы епсәләрҙә көсөргәнеш тура таяҡта булған көсөргәнештән түбәнерәк, ә эске епсәләрҙә күберәк.
Моменттан нормаль көсөргәнештәр:[31]:
- ,
Кәкре кендектә тулы нормаль көсөргәнештәр:
- .
Нейтраль ҡаттын кәкре радиусы [31]:
- .
Кәкре кендектә булған деформациялар:[31]:
ҡайҙа
- — асыл күсереүе
- — киҫелештен боролоу мөйөшө
Күп ваҡытта деформация табыу өсөн кәкрелеҡте иҫәпкә алмайҙар. Аркаларҙын күсәре төрлө була:
-
Циркуль, түңәрәк
-
Парабола
-
Овоид (геометрия), Коробовая
-
өсмөйөш
-
«үрмәле»
статик эше буйнса аркалар төрҙәре [32]:
-
өс шарнирлы
-
ике шарнирлы
-
өс шарнирлы

Аркалар түшәм өсөн ҡулланыу ваҡытта улар тигеҙ булған тейәүғә расчетлана.Арканың киҫелештә булған көсөргәнеште табыу өсөн формулалар:[32]:
1. Бөгөлөү момент
- ,
ҡайҙа
- — шарирһыҙ аркала таяныс моменты (ике һәм өс шарирлы аркала юҡ була)
- —таяҡ моменты
- —баҫым көсө (рус. распор)
- — киҫелеш координаталар
Баҫым көсө (рус. распор):[32]:
- ,
ҡайҙа
- — пролёттын уртаһында таяҡ моменты
- — арканыҡ күтәреү көйәнтәһе (рус. стрела подъёма арки)
- — араканың геометрияғы һәм физик күрһәткестәрҙе иҫәпкә алған коэффициенты
2. Буй көсө
- ,
ҡайҙа
- — арҡыры көс
- — угол между касательной к оси арки в рассматриваемой сечении и горизонталью.
3. Арҡыры көс
- .
Рама[үҙгәртергә | сығанаҡты үҙгәртеү]
Ҡаты рама төҙөлөш механикала load-resisting skeleton, тура йәки бөгөлгән өлөштәрҙән тора. Үҙ араһында кубеһе ҡаты бәйләнештәр менән берләштерелгән.
АҠШ Ҡорос конструкциялар коды, B3 бүлеге коментарийы буйынса,
Ks = Ms/θs
ҡайҙа
Ms = момент (N-mm)
θs = боролма мөйөшө
Ҡоролмалар теорияһы[үҙгәртергә | сығанаҡты үҙгәртеү]
Ҡоролмалар теорияһы — төҙөлөш механикаһының классик бүлеге. Ҡоролошҡа ике төрлө йөкләнеш йоһонто яһай:
- статик (Ҡоролмалар статикаһы)
- динамик (Ҡоролмалар динамикаһы), механиканың есемдәр хәрәкәте ҡанундарын өйрәнеүсе бүлеге
Динамик йөкләнештәр ҡоролмаға ҡурҡыныслы тиҙләнеш бирә.
Динамик йөкләнештәр төрҙәре[үҙгәртергә | сығанаҡты үҙгәртеү]
- машиналарҙан һәм механизмдарҙан эшләү ваҡытта вибрация (гармоник) йөкләнештәре
- машиналарҙан һәм механизмдарҙан эшләү ваҡытта һуғыу (импульс) йөкләнештәре
- шартлатыу тулҡындан тупраҡ аша йоғонто яһау
- сейсмик йоғонто яһау
- Ер тетрәү ваҡытта ҡоролмаға кинематика йоғонто яһау, уның нигеҙҙен урын алмаштырыу
- Ел йөкләнештәре
- Тулҡын йөкләнештәре
- Транспорт йөрөү ваҡытта йөкләнештәре
Динамик йөкләнештәр ҡоролма тирбәлеүенә килтерә. Ошо ваҡытта ҡоролманың нөктәләре урын алмаштыра; көсөргәнештәр, деформациялар үҙгәрә.
Бөтә дәүмәлдәрҙе һәр билдәләнгән ваҡытта табыу - ҡоролмалар теорияһының маҡсаты.
Ҡоролманың динамикаһының фараздар[үҙгәртергә | сығанаҡты үҙгәртеү]
Ҡоролманың динамикаһының фараздар статикала булһан фараздарзы ҡабатлай.
- Материалдын бер төрлөлөк, тотошлоҡ, изотропия (рус. однородность, сплошность,изотропность )
- Һығылмалылыҡ – юл буйынса буйһона
- Деформациялар һәм урын алмаштырыу эҙ
- Системалар юл буйнса деформациялана, суперпозиция принибы (рус. Системы считаються линейно деформируемыми, принцип суперпозиции)
- Масса бер урында туплау, ысынбарлыҡта юл буйынса тарала(рус. сосредоточение масс, при фактическом линейном распределении)
- Һығылмалылыҡ модуле статиканан табыла. Ысынбарлҡта ул юғарыраҡ. (рус. модуль упругости определяеться статикой, хотя фактически он больше)
- Энергия юғалтыу. Тирбәлеүҙәр ике төрлө ғенә була:
- баҫылмаған (фараз), Һығылмалы материал
- баҫылған, Һығылмалһыҙ материал
- Тимер-бетон ҡоролмаларҙа деформациялар бетон ҡоролмаларҙа деформациялар һымаҡ
Киҫкенлек коэффициенты[үҙгәртергә | сығанаҡты үҙгәртеү]
Киҫкенлек коэффициенты - тирбәлеүҙәр теорияһында үлсәүһеҙ скаляр физик дәүмәле:
ҡайҙа
- А — амплитуда
- А0 тигеҙләнеш амплитудаһы (P0 көстән статик деформацияғы)
- ω —асыуҙын йышлығы
- p — тирбәлеүҙен йышлығы
- n — үҙлелеҡте көсөн күрһәткән коэффициенты
Киҫкенлек коэффициенты асыу иткән көсөндөн йышлығынан үҙгәрештәрҙе табыу өсөн ҡулланыла. n коэффициенты табыу ҡыйын. n урынына йотолоу коэффицентты ψ ҡуялар
Логарифм декременты δ индерәбеҙ
киләбеҙ
ω асыу иткән көсөнөн йышлығы үҙ йышлыҡҡа p яҡынайтыу ваҡытта киҫкенлек коэффициенты үсә. ω/p=1 булһанда тирбәлеүҙәрҙен максимумы була
ҡайҙа
- δ — тирбәлеүҙәрҙен логарифм декременты
- ω — асыу йышлығы
- p — тирбәлеүҙәрҙен үҙ йышлығы
Энергетик системаһына ҡарап ошо дәүмәл системаның сифатлығы тип атала
Резонанс[үҙгәртергә | сығанаҡты үҙгәртеү]
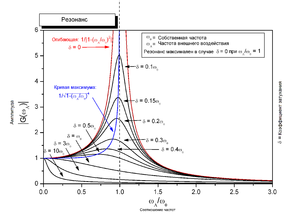
Резона́нс (франц. resonance, лат. resono — яуап, яуап биреү (ҡайтарыу)) — ирекһеҙ тирбәлеүҙәрҙен амплитудаһы киҫкен үҫеү, осцилляторҙын үҙ частотаһы һәм тышҡы йөкләнеш частотаһы уратҡлашыу ваҡытта. Амплитуда үҫеү – резонанстын һөҙөмтәһе.
Сәбәбе –тышҡы һәм эске частоталар уртаҡлыҡ булыу. Резонанс Галилео Галилей менән 1602 йылда беренсенән тикшерелде. Күп кешеләрғә оҫраған резонанс системаһы – бәүелсәктәр. Бәүелсәктәрҙе резонанс частотаға ярашлы этәреп – бәүелеү үҫә. Бәүелсәктәрҙен резонанс частотаһы:
- ,
g - (9,8 м/с²), L — маятникты элеп ҡуйып урындан уның массаһының үҙәгенә тиклем оҙонлоҡ.
Иҫкәрмәләр[үҙгәртергә | сығанаҡты үҙгәртеү]
- ↑ Ҡоролмаларҙын статикаһын, динамикаһын, тотороҡлоғон шулай уҡ төҙөлөш механикаһы тип атайҙар (тар мәғәнәғендә).
- ↑ http://www.matweb.com/search/datasheet.aspx?matguid=638937fc52ca4683bc0c3f18f54f5a24
- ↑ http://www.matweb.com/search/DataSheet.aspx?MatGUID=de22e04486ff4598a26027abc48e6382
- ↑ http://www.matweb.com/search/DataSheet.aspx?MatGUID=64583c8ce6724989a11e1ef598d3273d
- ↑ http://www.matweb.com/search/DataSheet.aspx?MatGUID=c140b20b165941c7a948e782eeced4ea
- ↑ http://www.matweb.com/search/datasheet.aspx?MatGUID=722e053100354c02a6d450d5d7646d82
- ↑ http://www.matweb.com/search/DataSheet.aspx?MatGUID=b141bfe746f142638fdc30ac59aa306e
- ↑ USStubular.com 2010 йыл 8 апрель архивланған.
- ↑ Beryllium I-220H Grade 2
- ↑ Aluminum 2014-T6
- ↑ 11,0 11,1 East Coast Fibreglass Supplies: Guide to Glass Reinforced Plastics 2015 йыл 16 февраль архивланған.
- ↑ Tube Properties
- ↑ Material Properties Data: Soda-Lime Glass
- ↑ Toray Properties Document 2011 йыл 17 июль архивланған.
- ↑ I Agnarsson, M Kuntner, T A Blackledge, Bioprospecting Finds the Toughest Biological Material: Extraordinary Silk from a Giant Riverine Orb Spider
- ↑ http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2716092/table/T3/
- ↑ Tensile and creep properties of ultra high molecular weight PE fibres 2007 йыл 27 сентябрь архивланған.
- ↑ Mechanical Properties Data 2007 йыл 3 май архивланған.
- ↑ Zylon Properties Document
- ↑ Uhu endfest 300 epoxy: Strength over setting temperature
- ↑ Fols.org 2011 йыл 25 июль архивланған.
- ↑ Lee, C. et al. (2008). «Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene». Science 321 (5887): 385–8. DOI:10.1126/science.1157996. PMID 18635798. . Lay summary.
- ↑ IOP.org Z. Wang, P. Ciselli and T. Peijs, Nanotechnology 18, 455709, 2007.
- ↑ 24,0 24,1 [1] 2015 йыл 21 сентябрь архивланған.
- ↑ Ржаницын А. Р. Составные стержни и пластины. М., Стройиздат, 1986.
- ↑ 26,0 26,1 Лишак В. И. Расчёт бескаркасных зданий с применением ЭВМ. М., Стройиздат, 1977.
- ↑ Пособие по проектированию жилых зданий. Вып. 3. Конструкции жилых зданий (к СНиП 2.08.01-85). М., Стройиздат,1989.
- ↑ Власов В. З. Тонкостенные пространственные системы. М., Госстройиздат, 1958.
- ↑ Лишак В. И. К расчету крупнопанельных зданий повышенной этажности – Строительная механика и расчет сооружений, 1969, № 1: с. 16-21.
- ↑ Вольфсон Б. П. Расчет зданий как сборных (монолитных) тонкостенных пространственных систем. – Строительная механика и расчет сооружений, 1972, № 5.
- ↑ 31,0 31,1 31,2 31,3 31,4 31,5 31,6 Беляев Н. М. Сопротивление материалов. Издательство Наука, 1965 год. Стр.584-590
- ↑ 32,0 32,1 32,2 Лебедева Н. В. Фермы, арки, тонкостенные пространственные конструкции. М.: Архитектура-С. 2006 год. Стр.24-35















![{\displaystyle n>\left[n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8ce80d583acbcd0e8e61a7a6fec23d5b93b921)
![{\displaystyle \left[n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73e0e48f35460bcb3ad75fb5b2b2c06a3ee1855a)




























































