Тигеҙләмә

Тигеҙләмә
Ҡайҙа өйрәнелә	элементар алгебра
Вики-проект	Проект:Математика[d]
Ҡапма-ҡаршыһы	неравенство
Тигеҙләмә Викимилектә

Тигеҙлек тамғаһының баҫмала беренсе Роберт Рекордтың китабында 1557 йылда күренеүе (14x + 15 = 71 тигеҙләмәһе яҙылған)

Тигеҙләмә —

$f\left(x_{1},x_{2}\dots \right)=g\left(x_{1},x_{2}\dots \right)$ күренешендәге тигеҙлек,

бында $f,g$ сифатында йышыраҡ һанлы функциялар сығыш яһай, әммә практикала ҡатмарлыраҡ осраҡтар ҙа осрай — мәҫәлән, вектор-функциялар өсөн тигеҙләмәләр, функциональ тигеҙләмәләр һәм башҡалар.

Тигеҙләмәне сығарыу

x = f(x) тигеҙләмәһенең тамырҙарын график ысул менән табыу иллюстрацияһы

Тигеҙләмәне сығарыу — аргументтарҙың, был тигеҙлек дөрөҫ булғандағы ҡиммәттәрен табыу буйынса мәсьәлә. Аргументтарҙың мөмкин булған ҡиммәттәренә өҫтәлмә шарттар ҡуйылыуы мөмкин (бөтөн һан булыу, ысын һан булыу һәм башҡалар).

Бирелгән функцияларҙың аргументтары (ҡайһы берҙә «үҙгәреүсәндәр» тип атайҙар) тигеҙләмә осрағында «билдәһеҙҙәр» тип аталалар.

Ҡалып:Якорь2.

Тамырҙар тураһында, улар бирелгән тигеҙләмәне ҡәнәғәтләндерәләр тип әйтәләр.

Тигеҙләмәне сығарыу уның бөтә сығарылыштары (тамырҙары) күмәклеген табыу йәки тамыры юҡ икәнен иҫбатлау тигән һүҙ.

Тиң көслө тигеҙләмәләр

Тамырҙары күмәклеге тап килгән тигеҙләмәләр тиң көслө йәки эквивалентлы тигеҙләмәләр тип аталалар. Тамырҙары булмаған тигеҙләмәләр ҙә шулай уҡ тиң көслө тигеҙләмәләр тип һаналалар.

Тигеҙләмәләрҙең эквивалентлығы симметриялылыҡ үҙсәнлегенә эйә: әгәр бер тигеҙләмә икенсеһенә эквивалентлы булһа, ул саҡта икенсе тигеҙләмә беренсеһенә эквивалентлы була.

Тигеҙләмәләрҙең эквивалентлығы транзитивлыҡ үҙсәнлегенә эйә: әгәр бер тигеҙләмә икенсеһенә эквивалентлы, ә икенсеһе өсөнсөһөнә эквивалентлы булһа, ул саҡта беренсе тигеҙләмә өсөнсөһөнә эквивалентлы була. Тигеҙләмәләрҙең эквивалентлылыҡ үҙсәнлеге, тигеҙләмәләрҙе сығарыу ысулының нигеҙендә ятҡан үҙгәртеүҙәрҙе башҡарырға мөмкинлек бирә.

Өсөнсө мөһим үҙсәнлеге теорема ярҙамында бирелә: әгәр $f,g$ функциялары бөтөнлөк өлкәһендә бирелһә, ул саҡта

$f(x)\cdot g(x)=0$ тигеҙләмәһе

$f(x)=0,\qquad g(x)=0$ тигеҙләмәләр йыйылмаһына эквивалентлы.

Был, беренсе тигеҙләмәнең бөтә тамырҙары ҡалған ике тигеҙләмәнең береһенең тамыры була тигәнде аңлата, һәм беренсе тигеҙләмәнең тамырын, һәр береһендә ябайыраҡ тигеҙләмәләр сығарып, ике бүлемдә сығарырға мөмкинлек бирә.

Төп үҙсәнлектәре

Тигеҙләмәгә ингән алгебраик аңлатмалар менән, уның тамырҙарын үҙгәртмәй торған ғәмәлдәр башҡарырға мөмкин, атап әйткәндә:

1. тигеҙләмәнең теләһә ҡайһы яғында йәйәләрҙе асырға мөмкин;
2. тигеҙләмәнең теләһә ҡайһы яғында оҡшаш быуындарҙы берләштерергә мөмкин;
3. тигеҙләмәнең теләһә ниндәй быуынын, тамғаһын ҡапма-ҡаршыға үҙгәртеп, тигеҙләмәнең бер яғынан икенсе яғына күсерергә мөмкин;
4. тигеҙләмәнең ике яғына ла бер үк аңлатманы ҡушырға мөмкин;
5. тигеҙләмәнең ике яғынан да бер үк аңлатманы алып ташларға мөмкин;
6. тигеҙләмәнең ике яғын да нулдән айырмалы бер үк һанға ҡабатларға йәки бүлергә мөмкин.

Был ғәмәлдәрҙең һөҙөмтәһендә килеп сыҡҡан тигеҙләмәләр баштағы тигеҙләмәгә эквивалентлы булалар. Әммә 4 һәм 5 үҙсәнлектәр өсөн сикләүҙәр бар: тигеҙләмәнең ике яғына ла бер үк аңлатманы ҡушыу осрағында (йәки тигеҙләмәнең ике яғынан да бер үк аңлатманы алыу осрағында), аңлатмаға ингән билдәһеҙ бирелгән тигеҙләмәнең тамырына тигеҙ булған ҡиммәт ҡабул иткәндә, аңлатманың мәғәнәһе булмаһа, баштағы тигеҙләмәгә эквивалентлы булмаған тигеҙләмә килеп сыға. Ләкин әгәр тигеҙләмәнең ике яғына ла бер үк аңлатманы ҡушһаң (йәки тигеҙләмәнең ике яғынан да бер үк аңлатманы алһаң), аңлатмаға ингән билдәһеҙ бирелгән тигеҙләмәнең тамырына тигеҙ булмаған ҡиммәт ҡабул иткәндә генә аңлатманың мәғәнәһе булмаһа, баштағы тигеҙләмәгә эквивалентлы булған тигеҙләмә килеп сыға.

Тигеҙләмәнең ике яғын да билдәһеҙ дәүмәл ингән аңлатмаға ҡабатлау йәки бүлеү, сит тамырҙар барлыҡҡа килеүенә йәки тамырҙарҙы юғалтыуға килтерергә мөмкин. Тигеҙләмәнең ике яғын да квадратҡа күтәреү сит тамырҙар барлыҡҡа килеүенә килтерергә мөмкин.

Тигеҙләмәнең эҙемтәһе һәм сит тамырҙар

$F\left(x\right)=G\left(x\right)$ тигеҙләмәһе

$f\left(x\right)=g\left(x\right)$ тигеҙләмәһенең эҙемтәһе тип атала,

әгәр икенсе тигеҙләмәнең бөтә тамырҙары беренсе тигеҙләмәнең тамырҙары булһа. Беренсе тигеҙләмәнең, икенсе тигеҙләмә өсөн сит тамырҙар булған, өҫтәлмә тамырҙары булырға мөмкин. Сит тамырҙар, тигеҙләмәнең тамырын табыу өсөн башҡарырға кәрәк булған үҙгәртеүҙәр ваҡытында барлыҡҡа килергә мөмкин. Уларҙы асыҡлау өсөн, тамырҙы баштағы тигеҙләмәгә ҡуйып ҡарап, тикшерергә кәрәк. Әгәр үҙгәреүсән урынына тамырҙы ҡуйғанда тигеҙләмә тождествоға әйләнһә, ул саҡта тамыр ысын, әгәр тождествоға әйләнмәһә — сит тамыр.

Миҫал

${\sqrt {2x^{2}-1}}=x$ тигеҙләмәһе ике яғын да квадратҡа күтәргәндә, $2x^{2}-1=x^{2}$ тигеҙләмәһен бирә, йәки $x^{2}=1$. Ике тигеҙләмә лә баштағы тигеҙләмәнең эҙемтәһе булып тора. Һуңғы тигеҙләмәне сығарыуы еңел; уның ике тамыры бар $x=1$ һәм $x=-1$.

Беренсе тамырҙы баштағы тигеҙләмәгә ҡуйғанда тождество барлыҡҡа килә ${\sqrt {1}}=1$. Икенсе тамырҙы баштағы тигеҙләмәгә ҡуйғанда дөрөҫ булмаған раҫлау килеп сыға ${\sqrt {1}}=-1$. Шулай итеп, икенсе тамырҙы сит тамыр булараҡ алып ташларға кәрәк.

Тигеҙләмәләрҙең төрҙәре

Алгебраик тигеҙләмәләр, параметрлы тигеҙләмәләр, трансцендент, функциональ, дифференциаль һәм башҡа төрҙәге тигеҙләмәләр була.

Тигеҙләмәләрҙең ҡайһы бер төрҙәренең аналитик сығарылыштары бар, улар тамырҙың теүәл ҡиммәтен биреү генә түгел, ә сығарылышты параметр инергә мөмкин булған формула рәүешендә яҙырға мөмкинлек биреүе менән дә уңайлы. Аналитик аңлатмалар тамырҙы иҫәпләргә генә түгел, ә параметрҙың ҡиммәтенә бәйле рәүештә, тамырҙың барлығын һәм һанын анализларға мөмкинлек бирә, был йыш ҡына практикала ҡулланыу өсөн, тамырҙың конкрет ҡиммәтен табыуға ҡарағанда ла мөһимерәк.

Аналитик сығарылыштары билдәле булған тигеҙләмәләргә дәрәжәһе дүрттән ҙур булмаған алгебраик тигеҙләмәләр инә: һыҙыҡлы, квадрат, куб тигеҙләмәләр һәм дүртенсе дәрәжә тигеҙләмәләр. Юғары дәрәжәләге алгебраик тигеҙләмәләрҙең дөйөм осраҡта аналитик сығарылыштары юҡ, әммә уларҙың ҡайһы берҙәрен түбәнерәк дәрәжәләге тигеҙләмәләргә килтерергә мөмкин. Трансцендент функциялар ингән тигеҙләмәләр трансцендент тигеҙләмәләр тип аталалар. Улар араһында ҡайһы бер тригонометрик тигеҙләмәләр өсөн аналитик сығарылыштар билдәле, сөнки тригонометрик функцияларҙың нулдәре яҡшы билдәле.

Дөйөм осраҡта, аналитик сығарылышты табып булмағанда, иҫәпләү (һанлы) ысулдары ҡулланалар. Һанлы ысулдар теүәл тамырҙы бирмәйҙәр, ә ни бары тамыр ингән интервалды алдан бирелгән билдәле ҡиммәткә тиклем тарайтырға ғына мөмкинлек бирәләр.

Алгебраик тигеҙләмәләр

Алгебраик тигеҙләмә тип

$P\left(x_{1},x_{2},\ldots ,x_{n}\right)=0$ күренешендәге тигеҙләмә атала,

бында $P$ — билдәһеҙҙәр тип аталған $x_{1},\ldots ,x_{n}$ үҙгәреүсәнле күпбыуын.

$P$ күпбыуынының коэффициенттары ғәҙәттә ниндәйҙер яландан  $F$ алына, һәм ул саҡта $P\left(x_{1},x_{2},\ldots ,x_{n}\right)=0$ тигеҙләмәһе  $F$ яланында алгебраик тигеҙләмә тип атала. Алгебраик тигеҙләмәнең дәрәжәһе тип  $P$ күпбыуынының дәрәжәһе атала.

Мәҫәлән,

$y^{4}+{\frac {xy}{2}}+y^{2}z^{5}+x^{3}-xy^{2}+{\sqrt {3}}x^{2}-\sin {1}=0$ тигеҙләмәһе ысын һандар яланында өс үҙгәреүсәнле (өс билдәһеҙле) етенсе дәрәжә алгебраик тигеҙләмә була.

Һыҙыҡлы тигеҙләмәләр

• дөйөм күренештә: $a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}+b=0$
• каноник күренештә: $a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}=b$

Квадрат тигеҙләмәләр

Файл:Квадратное уравнение.gif

$ax^{2}+bx+c=0,\quad a\neq 0$

бында $x$ — ирекле үҙгәреүсән, $a$, $b$, $c$ — коэффициенттар, шуның менән бергә $a\neq 0$.

$ax^{2}+bx+c$ аңлатмаһын квадрат өсбыуын тип атайҙар. Бындай тигеҙләмәнең тамыры (квадрат өсбыуындың тамыры) — $x$ үҙгәреүсәненең, квадрат өсбыуынды нулгә әйләндереүсе ҡиммәте, йәғни, квадрат тигеҙләмәне тождествоға әйләндереүсе ҡиммәте. Квадрат тигеҙләмәнең коэффициенттарының үҙҙәренең атамалары бар: $a$ коэффициентын беренсе йәки өлкән коэффициент, $b$ коэффициентын икенсе йәки $x$-тың коэффициенты, $c$-ны был тигеҙләмәнең ирекле быуыны тип атайҙар. Өлкән коэффициенты берәмеккә тигеҙ булған квадрат тигеҙләмәне килтерелгән квадрат тигеҙләмә тип атайҙар. Бындай тигеҙләмәне бөтә аңлатманы $a$ өлкән коэффициентҡа бүлеп килтереп сығарырға мөмкин: $x^{2}+px+q=0$, бында $p={\frac {b}{a}}$, ә $q={\frac {c}{a}}$. Бөтә коэффициенттары ла нулдән айырмалы булған тигеҙләмә тулы квадрат тигеҙләмә тип атала. Өлкән коэффициенттан башҡа бер генә коэффициенты булһа ла (йәки икенсе коэффициент, йәки ирекле быуын) нулгә тигеҙ булған квадрат тигеҙләмә тулы булмаған квадрат тигеҙләмә тип атала.

$ax^{2}+bx+c=0$ квадрат тигеҙләмәһенең тамырҙарын табыу өсөн, дөйөм осраҡта түбәндә килтерелгән алгоритмды ҡулланырға кәрәк:

Квадрат тигеҙләмәнең дискриминантын иҫәпләргә: уның өсөн дискриминант тип $D=b^{2}-4ac$ аңлатмаһы атала.

1) әгәр $D>0$	2) әгәр $D=0$	3) әгәр $D<0$
тамырҙары икәү, һәм уларҙы табыу өсөн ошо формуланы ҡулланалар $x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}(1)$	тамыры берәү (ҡайһы бер контекстарҙа ике тигеҙ йәки тап килеүсе тамырҙар тураһында һөйләйҙәр, йәки  2 тапҡырлы тамыр тураһында), һәм ул $-{\frac {b}{2a}}$-ға тигеҙ.	ул саҡта ысын һандар күмәклегендә тамыры юҡ.

Тура мөйөшлө координаталар системаһында $f\left(x\right)=ax^{2}+bx+c$ квадрат функцияһының графигы парабола була. Ул абсциссалар күсәрен $f\left(x\right)=0$ квадрат тигеҙләмәһенең тамырҙарына ярашлы нөктәләрҙә киҫеп үтә.

Куб тигеҙләмәләр

Кубик функцияның графигы

$ax^{3}+bx^{2}+cx+d=0,\quad a\neq 0$

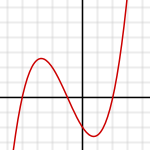
Кубик тигеҙләмәне тура мөйөшлө координаталарҙа график ысул менән анализлау өсөн кубик парабола ҡулланыла.

Был тигеҙләмәне $a$-ға бүлеп һәм $x=y-{\tfrac {b}{3a}}$ алмаштырып ҡуйыуын башҡарып, каноник күренештәге теләһә ниндәй куб тигеҙләмәне ябайыраҡ күренешкә килтерергә мөмкин

$y^{3}+py+q=0$,

. Шуның менән бергә коэффициенттары тигеҙ була:

$q={\frac {2b^{3}}{27a^{3}}}-{\frac {bc}{3a^{2}}}+{\frac {d}{a}}={\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}$,

$p={\frac {c}{a}}-{\frac {b^{2}}{3a^{2}}}={\frac {3ac-b^{2}}{3a^{2}}}$.

Дүртенсе дәрәжәләге тигеҙләмә

Дүрт тамыры һәм өс критик нөктәһе булған 4-се дәрәжә күпбыуындың графигы.

$f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.$

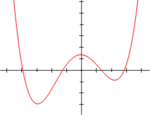
Дөйөм күренештә радикалдарҙа (йәғни коэффициенттарҙың теләһә ниндәй ҡиммәтендә) аналитик сығарылышы булған алгебраик тигеҙләмәләр өсөн дүртенсе дәрәжә иң юғары дәрәжә булып тора. $f\left(x\right)$ йоп дәрәжәле күпбыуын булғанлыҡтан, плюс һәм минус сикһеҙлеккә ынтылғанда уның сикләмәһе бер үк. Әгәр $a>0$ булһа, функция ике яҡтан да плюс сикһеҙлеккә тиклем үҫә, һәм тимәк, глобаль минимумы бар. Ошоға оҡшаш рәүештә, әгәр $a<0$ булһа, функция ике яҡтан да минус сикһеҙлеккә тиклем кәмей, һәм тимәк, глобаль максимумы бар.

Һыҙыҡлы алгебраик тигеҙләмәләр системалары

Тигеҙләмәләр системаһы күренеше:

${\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\dots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\dots +a_{2n}x_{n}=b_{2}\\\dots \\a_{m1}x_{1}+a_{m2}x_{2}+\dots +a_{mn}x_{n}=b_{m}\\\end{cases}}$

(1)

Бында $m$ — тигеҙләмәләр һаны, ә $n$ — билдәһеҙҙәр һаны. x₁, x₂, …, x_n — табырға кәрәк булған билдәһеҙҙәр. a₁₁, a₁₂, …, a_mn — системаның коэффициенттары — һәм b₁, b₂, … b_m — ирекле быуындар — билдәле тип фаразланалар. Система коэффициенттарының индекстары ярашлы рәүештә (a_ij) тигеҙләмәнең номерын (i) һәм был коэффициент торған билдәһеҙҙең номерын (j) күрһәтә.

Әгәр системаның бөтә ирекле быуындары нулгә тигеҙ булһа (b₁ = b₂ = … = b_m = 0), система тигеҙләмәләрҙең тиң системаһы тип атала; ҡалған осраҡта — тиң түгел. Әгәр m тигеҙләмәләр һаны билдәһеҙҙәр һаны n-гә тигеҙ булһа, система квадрат тип атала. Системаның сығарылышы — шундай n c₁, c₂, …, c_n һандары йыйылмаһы, һәр c_i ҡиммәтен x_i урынына системаға ҡуйғанда, системаның бөтә тигеҙләмәләре лә тождестволарға әйләнәләр. Әгәр системаның бер генә булһа ла сығарылышы булһа, система берләштерелгән тип атала, һәм әгәр бер генә лә сығарылышы булмаһа, берләштерелмәгән тип атала. Әгәр түбәндәге тигеҙлектәрҙең береһе булһа ла боҙолһа, берләштерелгән тигеҙләмәләр системаһының c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ сығарылыштары төрлө тип атала:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Әгәр системаның бер генә сығарылышы булһа, берләштерелгән система аныҡ тип атала; әгәр уның ике булһа ла төрлө сығарылышы булһа, ул аныҡ булмаған система тип атала. Әгәр тигеҙләмәләр һаны билдәһеҙҙәр һанынан күберәк булһа, ул аныҡ булмаған тип атала.

Параметрлы тигеҙләмәләр

Параметрлы тигеҙләмә тип, тышҡы күренеше һәм сығарылышы бер йәки бер нисә параметрға бәйле булған математик тигеҙләмә атала. Параметрлы тигеҙләмәне сығарыу түбәндәгене аңлата:

1. Был тигеҙләмәнең сығарылышы булғандағы параметрҙарҙың бөтә ҡиммәттәре системаһын табыу.
2. Параметрҙарҙың табылған һәр ҡиммәттәр системаһы өсөн бөтә сығарылыштарын табыу, йәғни билдәһеҙ һәм параметр өсөн үҙҙәренең мөмкин булған ҡиммәттәре өлкәһе күрһәтелергә тейеш.

Параметрлы тигеҙләмәләр һыҙыҡлы, шулай уҡ һыҙыҡлы булмаған булырға мөмкин. Һыҙыҡлы параметрлы тигеҙләмәгә миҫал:

$a\,x+1=4,$

Һыҙыҡлы булмаған параметрлы тигеҙләмәгә миҫал:

${\mbox{log}}_{x^{2}}{\frac {a+3}{7-x}}=5,$

бында $x$ — бәйләнешһеҙ үҙгәреүсән, $a$ — параметр.

Трансцендент тигеҙләмәләр

Алгебраик булмаған тигеҙләмә трансцендент тигеҙләмә тип атала. Ғәҙәттә улар күрһәткесле, логарифмик, тригонометрик, кире тригонометрик функциялар ингән тигеҙләмәләр, мәҫәлән:

• $\cos x=x$
• $\lg x=x-5$
• $2^{x}=\lg x+x^{5}+40$

Ҡәтғиерәк билдәләмә ошолай: трансцендент тигеҙләмә — ул $f\left(x\right)=g\left(x\right)$ күренешендәге тигеҙләмә, бында $f$ һәм $g$ функциялары аналитик функциялар, һәм уларҙың береһе генә булһа ла алгебраик функция түгел.

Функциональ тигеҙләмәләр

Функциональ тигеҙләмә тип, функцияның (йәки функцияларҙың) бер нөктәләге ҡиммәте менән уның башҡа нөктәләрҙәге ҡиммәттәре араһында бәйләнеште күрһәтеүсе тигеҙләмә атала. Был функциялар ҡәнәғәтләндергән функциональ тигеҙләмәләрҙе тикшереп, функцияларҙың күп үҙсәнлектәрен асыҡларға мөмкин. «Функциональ тигеҙләмә» термины ғәҙәттә ябай ысулдар менән алгебраик тигеҙләмәләргә килтереп булмаған тигеҙләмәләр өсөн ҡулланыла. Был килтереп булмағанлыҡ йыш ҡына, тигеҙләмәлә билдәһеҙ функцияның аргументтары булып бәйләнешһеҙ үҙгәреүсәндәр үҙҙәре түгел, ә уларҙың ҡайһы бер функциялары тороуы менән бәйле. Мәҫәлән:

$f\left(s\right)=2^{s}\pi ^{s-1}\sin \left({\frac {\pi s}{2}}\right)\Gamma \left(1-s\right)f\left(1-s\right)$ функциональ тигеҙләмәһен,

бында $\Gamma (z)$ — Эйлерҙың гамма-функцияһы, Римандың дзета-функцияһы  ζ ҡәнәғәтләндерә.

• Артабанғы өс тигеҙләмәне гамма-функция ҡәнәғәтләндерә; ул был өс тигеҙләмә системаһының берҙән бер сығарылышы булып тора :

$f\left(x\right)={f\left(x+1\right) \over x}$

$f\left(y\right)f\left(y+{\frac {1}{2}}\right)={\frac {\sqrt {\pi }}{2^{2y-1}}}f\left(2y\right)$

$f\left(z\right)f\left(1-z\right)={\pi \over \sin \left(\pi z\right)}$ (Эйлерҙың тултырыу формулаһы).

$f\left({az+b \over cz+d}\right)=\left(cz+d\right)^{k}f\left(z\right)$ функциональ тигеҙләмәһе,

бында $a$, $b$, $c$, $d$, $ad-bc=1$, йәғни ${\begin{vmatrix}a&b\\c&d\end{vmatrix}}=1$ тигеҙлеген ҡәнәғәтләндергән бөтөн һандар, $f$-ты  k тәртибендәге модуляр форма булараҡ билдәләй.

Дифференциаль тигеҙләмәләр

Дифференциаль тигеҙләмә тип, ниндәйҙер билдәһеҙ функцияның ниндәйҙер нөктәләге ҡиммәтен уның төрлө тәртиптәге сығарылмаларының шул уҡ нөктәләге ҡиммәте менән бәйләүсе тигеҙләмә атала. Дифференциаль тигеҙләмәнең яҙылышына билдәһеҙ функция, уның сығарылмалары һәм бәйләнешһеҙ үҙгәреүсәндәр инә. Дифференциаль тигеҙләмәнең тәртибе — уға ингән сығарылмаларҙың иң ҙур тәртибе.  n тәртибендәге дифференциаль тигеҙләмәнең сығарылышы тип, ниндәйҙер  (a, b) интервалында $y'\left(x\right),y''\left(x\right),\dots ,y^{\left(n\right)}\left(x\right)$  n-ды ла индереп  n-ға тиклемге сығарылмалары булған һәм был тигеҙләмәне ҡәнәғәтләндергән $y\left(x\right)$ функцияһы атала. Дифференциаль тигеҙләмәне сығарыу процесы интеграллау тип атала.

Бөтә дифференциаль тигеҙләмәләр бүленәләр:

• ғәҙәттәге дифференциаль тигеҙләмәләргә (ОДУ), уларға тик бер аргументтың функциялары (һәм уларҙың сығарылмалары) инә:

$F\left(x,y,y',y'',...,y^{(n)}\right)=0$ йәки $F\left(x,y,{\frac {\mathrm {d} y}{\mathrm {d} x}},{\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}},...,{\frac {\mathrm {d} ^{n}y}{\mathrm {d} x^{n}}}\right)=0$,

бында $y=y\left(x\right)$ — $x$ бәйләнешһеҙ үҙгәреүсәненә бәйле булған билдәһеҙ функция (бәлки, вектор-функция; был осраҡта йыш ҡына дифференциаль тигеҙләмәләр системаһы тураһында һөйләйҙәр); штрих  $x$ буйынса дифференциаллауҙы аңлата.

• һәм Айырым сығарылмаларҙа дифференциаль тигеҙләмәләр, уларға ингән функциялар күп үҙгәреүсәндәргә бәйле:

$F\left(x_{1},x_{2},\dots ,x_{m},z,{\frac {\partial z}{\partial x_{1}}},{\frac {\partial z}{\partial x_{2}}},\dots ,{\frac {\partial z}{\partial x_{m}}},{\frac {\partial ^{2}z}{\partial x_{1}^{2}}},{\frac {\partial ^{2}z}{\partial x_{1}\partial x_{2}}},{\frac {\partial ^{2}z}{\partial x_{2}^{2}}},\dots ,{\frac {\partial ^{n}z}{\partial x_{m}^{n}}}\right)=0$,

бында $x_{1},x_{2},\dots ,x_{m}$ — бәйләнешһеҙ үҙгәреүсәндәр, ә $z=z\left(x_{1},x_{2},\dots ,x_{m}\right)$ — был үҙгәреүсәндәрҙең функцияһы.

Беренсе башлап дифференциаль тигеҙләмәләр механика мәсьәләләренән килеп сыҡҡан, уларҙа ваҡыттың функциялары итеп ҡаралған есемдәрҙең координаталары, уларҙың тиҙлектәре һәм тиҙләнештәре ҡатнаша.

Тигеҙләмәләргә миҫалдар

• $x+3=2x$
• $x^{2}+1=0$
• $e^{x+y}=x+y$
• $a^{n}+b^{n}=c^{n}$, бында $a,b,c,n$ — натураль һандар

Шулай уҡ ҡарағыҙ

• Диофант тигеҙләмәһе
• Һыҙыҡлы тигеҙләмә
• Квадрат тигеҙләмә
• Ниндәй ҙә булһа тигеҙләмәне төҙөү ярҙамында сығарыу
• Тигеҙләмәләр системаһы
• Үҙгәреүсән

Әҙәбиәт

• Бекаревич А. Б. Уравнения в школьном курсе математики. — Минск: Нар. асвета, 1968. — 152 с.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Маркушевич, Л. А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л. А. Маркушевич, Р. С. Черкасов. / Математика в школе. — 2004. — № 1.

Һылтанмалар

• [ Уравнение] — Ҙур совет энциклопедияһында мәҡәлә
• Уравнения // Энциклопедия Кольера. — Открытое общество. 2000.
• Уравнение // Энциклопедия Кругосвет
• Уравнение // Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
• EqWorld — Мир математических уравнений — содержит обширную информацию о математических уравнениях и системах уравнений.