Ябай һан

Нулдән йөҙгә тиклем бөтөн һандар. Ябай һандар ҡыҙыл төҫтә.

42 һанын ябай ҡабатлашыусыларға тарҡатыу: $42=2\times 3\times 7$

Ябай һан — ике генә бүлеүсеһе — берәмек һәм үҙе булған натураль (ыңғай бөтөн) һан. Икенсе төрлө әйткәндә, әгәр $x$ һаны $1$-ҙән ҙур һәм тик $1$-гә һәм $x$-ҡа ғына ҡалдыҡһыҙ бүленһә, ул ябай һан була. Миҫалға, $5$ — ябай һан, ә $6$ ябай һан түгел, сөнки $1$-ҙән һәм $6$-нан башҡа, ул $2$-гә һәм $3$-кә бүленә.

Арифметиканың төп теоремаһы ябай һандарҙың һандар теорияһында үҙәк ролен билдәләй: $1$-ҙән ҙур булған теләһә ниндәй бөтөн һан, йә ябай һан була, йә ябай һандарҙың ҡабатландығы итеп күрһәтелә ала, һәм ул ҡабатлашыусыларҙың тәртибенә тиклем аныҡлыҡ менән берҙән бер. Ошо теоремала тап берҙән-берлекте тәьмин итеү өсөн, берәмек ябай һан булып иҫәпләнмәй (кире осраҡта теләһә ниндәй тарҡатмаға ирекле һанда күп итеп берәмекте индерергә мөмкин, мәҫәлән, $3=1\cdot 3=1\cdot 1\cdot 3$ һәм башҡа шулай).

Берҙән ҙур һәм ябай булмаған натураль һандар ҡушма тип аталалар. Шулай итеп, бөтә натураль һандар өс класҡа бүленә: берәмеккә (бер генә натураль бүлеүсеһе булған), ябай һандарға (ике натураль бүлеүсеһе булған) һәм ҡушма һандарға (икенән күберәк натураль бүлеүсеһе булған). Ябай һандарҙың үҙсәнлектәрен өйрәнеү менән һандар теориһы шөғөлләнә. Ябай һандар ҙа, ҡушма һандар ҙа сикһеҙ күп.

Ябай һандар эҙмә-эҙлелеге ошолай башлана:

<!—1 һаны ябай түгел! -->2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199…

Һандың ябай булыу үҙсәнлеге ябайлыҡ тип атала. Бирелгән n һанының ябайлығын тикшереүҙең ябай, ләкин яй ысулы бүлеүселәрҙе берәмтекләп ҡарау; файҙалыраҡ алгоритмдар аҫтараҡ һүрәтләнгән.

Ябай һандарға ҡағылышлы күп проблемалар асыҡ ҡалалар, түбәндә ҡарағыҙ.

Ябай һандар математикала һәм яҡын фәндәрҙә киң ҡулланылалар. Мәҫәлән, асыҡ асҡыслы криптосистема кеүек бик күп мәғлүмәт технологиялары алгоритмдарында. Ул һандарҙы ябай ҡабатлашыусыларға тарҡатыуҙың ҡатмарлылығы кеүек үҙсәнлектәрҙе файҙалана.

Ирекле ҡулсалар һәм башҡа алгебраик структуралар өсөн ябай һан төшөнсәһен дөйөмләштереүҙәр бар, түбәндә ҡарағыҙ.

Тарихы

Ябай һан төшөнсәһе ҡасан индерелеүе билдәһеҙ, әммә ундай һандарҙы аңлау тураһында дәлилдәр һуңғы палеолитҡа ҡарай, быны Ишанго төймәһе раҫлай.

Боронғо мысырлыларҙың һаҡланып ҡалған яҙмаларында уларҙың ябай һандар тураһында ҡайһы бер мәғлүмәттәргә эйә булыуына ишара бар: мәҫәлән, беҙҙең эраға тиклем II меңйыллыҡҡа ҡараған Райнд папирусында 2/n күренешендәге кәсерҙәрҙе числителдәре бергә тигеҙ булған һәм төрлө знаменателле ике, өс йәки дүрт кәсерҙең суммаһы рәүешендә күрһәтеүсе таблицалар бар. Кәсерҙәрҙең знаменателдәренең уртаҡ бүлеүсеһе булған тарҡалмалары, мысырлыларҙың ябай һан менән ҡушма һан араһындағы айырманы белеүҙәрен күрһәтә.

Оксиринхта табылған Евклидтың "Башланғыстар"ының фрагменты

Ләкин ябай һандар тураһында һаҡланған иң иртә тикшеренеүҙәр боронғо гректарҙан алынған. Евклидтың «Башланғыстар»ында (б. э. т. 300 йылдар тирәһе.), ябай һандарҙың сикһеҙлеген, Евклид леммаһын һәм арифметиканың төп теоремаһын да индереп, ябай һандар тураһында мөһим теоремалар бар. Боронғо Грецияла шулай уҡ Эратосфен иләге — 1-ҙән алып n-ға тиклем бөтә ябай һандарҙы табыуҙың ябай алгоритмы уйлап табылған.

Пьер Ферма

Гректарҙан һуң XVII быуатҡа тиклем ябай һандарҙы өйрәнеүҙә ҙур яңылыҡтар булмай. 1640 йылда Пьер де Ферма (иҫбатламайынса) Ферманың бәләкәй теоремаһын (уны аҙағыраҡ Лейбниц һәм Эйлер иҫбатлай) һәм ике квадраттың суммаһы тураһында теореманы әйтеп бирә. Ферма шулай уҡ $2^{2^{n}}$+ 1 күренешендәге бөтә һандар — ябай (улар Ферма һандары тип аталалар) тигән фараз әйтә һәм уны n = 4-кә тиклем (йәғни $2^{16}$+ 1) иҫбат итә. Ләкин Эйлер n = 5 булғандағы артабанғы Ферма һаны (йәғни $2^{32}$ + 1) ҡушма һан булыуын күрһәтә (641-гә бүленә). Бөгөнгө көндә ябай булған башҡа билдәле Ферма һандары юҡ. Шул уҡ ваҡытта француз монахы Марен Мерсенн 2^p — 1, бында p — ябай һан, күренешендәге ябай һандарға иғтибар итә (бындай күренештәге бөтә һандар ҙа ябай түгел). Уларҙы Мерсенн хөрмәтенә Мерсендың ябай һандары тип атайҙар.

Эйлерҙың һандар теорияһындағы хеҙмәтенә ябай һандар тураһында бик күп мәғлүмәт ингән. Ул 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + … сикһеҙ рәт таралыусан булыуын күрһәтә. Шулай уҡ 1747 йылда ул йоп камил һандар —$2^{p-1}(2^{p}-1)$ күренешендәге бөтөн һандар икәнен күрһәтә, бында икенсе ҡабатлашыусы Мерсенндың ябай һаны булып тора. Эйлерҙың Христиан Гольдбах менән үҙ-ара яҙышҡан хаттарында Гольдбах билдәле Гольдбах гипотезаһын әйтеп бирә. Гипотеза 4-тән башлап теләһә ниндәй йоп һанды ике ябай һандың суммаһы рәүешендә күрһәтергә мөмкин тип раҫлай, һәм ул әлегә тиклем иҫбат ителмәгән.

XIX быуат башынан күп математиктар иғтибарын ябай һандарҙың асимптотик таралыуын өйрәнеүгә йүнәлтә. Лежандр һәм Гаусс, бер-береһенә бәйһеҙ рәүештә, ябай һандарҙың тығыҙлығы уртаса натураль логарифмға кире пропорциональ дәүмәлгә яҡын тигән фараз әйтәләр.

Оҙаҡ ваҡыт ябай һан саф математиканан ситтә әҙ ҡулланыла тип иҫәпләнә. Хәл 1970-се йылдарҙа, асыҡ асҡыслы криптография концепцияһы барлыҡҡа килгәс үҙгәрә, унда ябай һандар RSA шифрлау алгоритмы кеүек тәүге алгоритмдарҙың нигеҙен тәшкил итә.

Натураль һандарҙы ябай һандар ҡабатландығына тарҡатыу

Натураль һандарҙы ябай һандар ҡабатландығы рәүешендә күрһәтеү ябай ҡабатлашыусыларға тарҡатыу йәки һандарҙы факторизациялау тип атала. Хәҙерге ваҡытта һандарҙы факторизациялауҙың полиномиаль алгоритмдары билдәле түгел, ундай алгоритмдарҙың юҡ икәнлеге лә иҫбатланмаған. Фараз ителгән ҙур иҫәпләү ҡатмарлылығында факторизациялау мәсьәләләре RSA һәм ҡайһы бер башҡа криптосистемаларға нигеҙләнә. Полиномиаль ҡатмарлыҡтағы факторизациялау теоретик квантлы компьютерҙа Шор алгоритмы ярҙамында мөмкин.

Арифметиканың төп теоремаһы

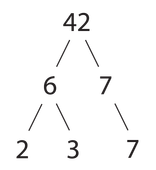
Арифметиканың төп теоремаһы, берәмектән ҙурыраҡ булған һәр натураль һан, ябай һандарҙың ҡабатландығы рәүешендә күрһәтелә ала, шуның менән бергә ҡабатлашыусыларҙың урынлашыу тәртибенә тиклем аныҡлыҡ менән берҙән-бер ысул менән тип раҫлай. Шулай итеп, ябай һандар натураль һандарҙың элементар «төҙөүсе блоктары» булып торалар. Мәҫәлән:

$23244$	$=2\cdot 2\cdot 3\cdot 13\cdot 149$
	$=2^{2}\cdot 3\cdot 13\cdot 149$. ($2^{2}$ $2$-нең квадратын йәки икенсе дәрәжәһен аңлата.)

Был миҫалда күрһәтелгәнсә, бер үк ябай бүлеүсе бер нисә тапҡыр ҡабатланырға мөмкин.

n һанының (сикле һандағы) p₁, p₂, … ,p_t ябай ҡабатлашыусыларына тарҡалмаһы n = p₁ • p₂ • ... • p_t n һанын ябай ҡабатлашыусыларға тарҡатыу тип атала. Арифметиканың төп теоремаһын ошолай итеп үҙгәртеп әйтергә мөмкин: ябай һандарға теләһә ниндәй тарҡалма бүлеүселәр тәртибенә тиклем аныҡлыҡ менән тождестволы була. Практикала күпселек һандар өсөн ябай ҡабатлашыусыларға тарҡатыуҙың күп ябай алгоритмдары бар, улар бөтәһе лә бер үк һөҙөмтәне бирә.

Берәмектең ябайлығы

Боронғо гректарҙың күпселеге $1$-ҙе һан тип иҫәпләмәгән, шуға күрә улар уны ябай тип иҫәпләй алмаған. Урта быуаттарҙа һәм Яңырыу дәүерендә күп математиктар $1$-ҙе беренсе ябай һан сифатында индерәләр. XVIII быуат уртаһында Христиан Гольдбах үҙенең Леонардом Эйлером менән данлыҡлы хатлашыуында $1$-ҙе беренсе ябай һан сифатында теҙмәгә индерә; әммә Эйлер үҙе $1$-ҙе ябай һан тип иҫәпләмәй. XIX быуатта күп математиктар элеккесә $1$ һанын ябай һан тип иҫәпләй. Мәҫәлән, Деррик Норман Лемерҙың 1956 йылда ҡабатлап баҫылған $10006721$-гә тиклем ябай һандар теҙмәһе беренсе ябай һан сифатында $1$-ҙән башланған. Анри Лебег $1$-ҙе ябай һан тип атаған һуңғы математик тип әйтәләр. XX быуат башына математиктар $1$ ябай һан түгел, ә үҙенең махсус категорияһын — «берәмек»те булдыра тигән ypmaҡ фекергә килә башлайҙар.

Әгәр $1$-ҙе ябай һан тип иҫәпләгәндә, Евклидтың арифметика тураһында төп теоремаһы (юғарыла телгә алынған) үтәлмәйәсәк. Мәҫәлән, $15$ һаны 3 • 5 һәм 1 • 3 • 5 тип тарҡатыла аласаҡ. Әгәр $1$ ябай һан булһа, был ике вариант $15$ һанының төрлө факторизацияһы тип иҫәпләнер ине, ошонан сығып был теореманың раҫлауын үҙгәртергә тура килер ине. Тап шулай уҡ, әгәр $1$ ябай һан тип иҫәпләнһә, Эратосфен иләге дөрөҫ эшләмәҫ ине: иләктең $1$ ябай һан тип фараз иткән модификацияланған версияһы, $1$-гә тапҡырлы булған бөтә ҡабатлашыусыларҙы (йәғни бөтә башҡа һандарҙы) төшөрөп ҡалдыра һәм һөҙөмтәлә бер генә ябай һанды — $1$-ҙе бирә. Бынан тыш, ябай һандар $1$ һанына хас булмаған, һандың уның ярашлы ҡиммәтенә сағыштырмаһы (Эйлер функцияһы) йәки суммаһы (бүлеүселәр функцияһы) кеүек бер нисә үҙсәнлеккә эйә.

Ябай һандарҙы эҙләү һәм таныу алгоритмдары

Эратосфен Киренский

Ниндәйҙер ҡиммәткә тиклем ябай һандарҙың башланғыс теҙмәһен табыуҙың ябай ысулдары Эратосфен иләге, Сундарам иләге һәм Аткин иләге.

Әммә, практикала ябай һандар теҙмәһен табыу урынына, йыш ҡына бирелгән һан ябай һанмы икәнен тикшереү талап ителә. Был мәсьәләне хәл итеүсе алгоритмдар ябайлыҡ тесы (|тест простоты) тип аталалар. Бик күп полиномиаль ябайлыҡ тестары бар, ләкин уларҙың күпселеге ихтималлыҡ алгоритмы (мәҫәлән, Миллер — Рабин тесы) һәм криптография ихтыяжы өсөн ҡулланылалар. 2002 йылда ябайлыҡҡа тикшереү мәсьәләһе дөйөм күренештә полиномиаль хәл итерлек икәне иҫбат ителә, ләкин тәҡдим ителгән аныҡлаусы Агравал — Каял — Саксена тесы ҙур иҫәпләү ҡатмарлылығы тыуҙыра, был уның практик ҡулланылышын ҡыйынлаштыра.

Ҡайһы бер һандар кластары өсөн махсуслаштырылған һөҙөмтәле ябайлыҡ тестары бар (түбәндә ҡарағыҙ).

Ябайлыҡ тесы

Ябайлыҡ тесы (йәки ябайлыҡты тикшереү) тип, индерелгән һандың ҡушма булыуы тураһында фаразды дөрөҫләмәҫкә, йәки уның ябай булыуын аныҡ раҫларға мөмкинлек биреүсе алгоритм атала. Икенсе осраҡта ул ысын ябайлыҡ тесы тип атала. Ябайлыҡ тесы мәсьәләһе P ҡатмарлылыҡ класына ҡарай, йәғни уны хәл итеү алгоритмының эш ваҡыты, 2002 йылда иҫбат ителгәнсә, индереү мәғлүмәттәренең күләменә бәйле. Полиномиаль алгоритмдың барлыҡҡа килеүе полиномиаль ябайлыҡ сертификаттарының булыуы менән, һәм, һөҙөмтә булараҡ, һанды ябайлыҡҡа тикшереү мәсьәләһе бер үк ваҡытта NP һәм co-NP кластарына ҡарауы сәбәпле прогнозланған.

Ғәмәлдә булған һанды ябайлыҡҡа тикшереү алгоритмдарын ике категорияға бүлергә мөмкин: ысын ябайлыҡ тесы һәм ихтималлыҡ тестары. Ысын ябайлыҡ тестарының һөҙөмтәһе булып һәр ваҡыт һандың ябай йәки ҡушма булыу факты тора. Ихтималлыҡ тесы һандың ябай булыуын ниндәйҙер ихтималлыҡ менән күрһәтә. Ябайлыҡтың ихтималлыҡ тесын ҡәнәғәтләндереүсе, ләкин ҡушма һандар ялған ябай һандар тип аталалар. Одним из примеров таких чисел являются числа Кармайкла.

Мерсенн һандары өсөн Люк-Лемер тесы ысын ябайлыҡ тестары миҫалдарының береһе булып тора. Очевидный недостаток Был тестың төп етешһеҙлеге уның билдәле бер төрҙәге һандарға ғына ҡулланылышында. Башҡа миҫалдар араһынан Ферманың бәләкәй теоремаһына нигеҙләнгәндәрен килтерергә мөмкин

• Ферма һандары өсөн Пепин тесы
• Прот һандары өсөн Прот теоремаһы
• Агравал — Каял — Саксена тесы, тәүге универсаль, полиномиаль, билдәләүсе һәм шартһыҙ ябайлыҡ тесы.
• Люк — Лемер — Ризель тесы

Шулай уҡ:

• Бүлеүселәрҙе эҙләү ысулы
• Вильсон Теоремаһы
• Поклингтон критерийы
• Миллер тесы (һандар теорияһы)
• Адлеман — Померанс — Румель тесы, Коэн һәм Ленстра Арьен тарафынан камиллаштырылған
• Эллиптик кәкреләрҙе ҡулланып ябайлыҡ тесы.

Ихтималлыҡ тестарына ҡарайҙар:

• Ферма тесы
• Миллер — Рабин тесы
• Соловей — Штрассен тесы
• Бейль — Померанц — Селфридж — Уогстафф тесы

Ҙур ябай һандар

Күп быуаттар дауамында «ҙур» ябай һандарҙы эҙләү математиктарҙа ҡыҙыҡһыныу уята. Һуңғы тиҫтә йылдарҙа бындай һандарҙы RSA кеүек шифрлауҙың ҡайһы бер алгоритмдарында ҡулланыу арҡаһында был тикшеренеүҙәр ғәмәли ҡиммәткә эйә була.

XVII быуатта Марен Мерсенн, тик n 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 и 257 һандарына тигеҙ булған осраҡтарҙа ғына (n ≤ 257 булғанда) $2^{n}-1$ күренешендәге һандар ябай була тип фараз итә Фараздың дөрөҫлөгөн тикшереү ул осорҙоң мөмкинлегенән күпкә юғары була. Тик XX быуатта ғына гипотеза яңылыш булыуы, һәм, моғайын, «һуҡырҙарса» эшләнеүе асыҡлана, сөнки Мерсенн өс осраҡты иҫәпкә алмай (n = 61, 89 һәм 107 өсөн); бынан тыш, n = 67 һәм n = 257 ярашлы һандар — ҡушма булып сыҡҡан.

1876 йылда Люка Франсуа Эдуард Анатоль M ₁₂₇ һаны (39-урынлы һан) — ябай булыуын иҫбат иткән, ул 1951 йылда ${\frac {2^{148}+1}{17}}$ (44 цифр) һәм, бер аҙ һуңғараҡ, $180*(2^{127}-1)^{2}+1$ (79 цифрҙан тора) һандары — электрон калькулятор ярҙамында табылған һуңғы ябай һан, табылғанға тиклем, иң ҙур билдәле ябай һан булып ҡала. Ул ваҡыттарҙан һуң артабанғы ябай һандар компьютер ярҙамында асыҡланалар: 1952 йылдан (SWAC M ₅₂₁ ябай һан булыуын күрһәтә), 1996 йылға тиклем улар суперкомпьютер тарафынан табылалар, һәм улар бөтәһе лә, 1989 һәм 1992 йылдар араһында рекорд булған $391581*2^{216193}-1$ һанынан башҡа, Мерсенн ябай һандары булалар (Люк-Лемер тесын, бындай һандар өсөн махсус алгоритмды ҡулланып табылған).

Ябай һандарҙы табыу алгоритмдары

Математиканың факторизация ҡулланыусы ҡайһы бер мәсьәләләре осраҡлы рәүештә һайлап алынған бер нисә бик ҙур ябай һанды талап итәләр. Уларҙы табыу алгоритмы Бертран постулатына нигеҙләнгән (Натураль n ≥ 2 өсөн n < p < 2n интервалында p ябай һаны табыла.):

Алгоритм: Индереү: $N$ натураль һаны Сисеү (P осраҡлы ябай һанды эҙләү) $P\gets$ $[N,2N]$ киҫегендә ирекле натураль һанды генерациялау функцияһы Әгәр $P$ ҡушма булһа, ул саҡта $P\leftarrow \,P+1$ Әгәр $P=2N$ булһа ул саҡта $P\leftarrow \,N$ Ҡайтыу «$P$ — осраҡлы ябай һан»

Был алгоритм менән мәсьәләне хәл итеү ваҡыты билдәһеҙ, ләкин етерлек ябай һандар булғанда һәм улар әҙме-күпме тигеҙ таратылған хәлдә, ул һәр саҡ ҙур ихтималлыҡ менән полиномиаль. Осраҡлы ябай һандар өсөн был шарттар үтәлә.

Ябай һандарҙы төҙөүҙең иң һөҙөмтәле ысулы булып бер аҙ үҙгәртелгән Ферманың бәләкәй теоремаһы тора.

N, S — таҡ натураль һандар булһын, ти. N-1 = S*R, шуның менән бергә S һанының һәр ябай q бүлеүсеһе өсөн шундай $a$ бөтөн һаны бар, бында

$a^{N-1}=1{\pmod {N}}$, $\gcd(a^{{\frac {N-1}{q}}-1},n)=1$

Ул саҡта N һанының һәр p ябай бүлеүсеһе түбәндәге сағыштырыуҙы ҡәнәғәтләндерә

$p=1{\pmod {2S}}$

Эҙемтә. Әгәр Ферма теоремаһының шарттары үтәлһә һәм $R\leqslant 4S+2$ булһа, ул саҡта N — ябай һан.

Хәҙер һуңғы раҫлау ярҙамында, ҙур $S$ ябай һаны булғанда, нисек итеп һиҙелерлек ҙурыраҡ $N$ ябай һанын төҙөргә мөмкин булыуын күрһәтәйек. Бының өсөн $R\leqslant 4S+2$ аралығында осраҡлы рәүештә $R$ йоп һанын һайлап алабыҙ һәм әйтәйек $N=SR+1$. Артабан $N$ һанының бәләкәй ябай бүлеүселәре юҡлығын тикшерәйек, бының өсөн уны бәләкәй ябай һандарға бүлеп ҡарайбыҙ; $N$ һанын Рабин алгоритмы ярҙамында бер нисә тапҡыр һанап ҡарайбыҙ. Әгәр был ваҡытта $N$ — ҡушма һан булыуы асыҡланһа, $R$-ҙың яңы ҡиммәтен һайлап алырға кәрәк һәм яңынан иҫәпләүҙәрҙе ҡабатларға кәрәк. Быны Рабин алгоритмы һынауын күп тапҡыр үткән N һаны табылғанға тиклем башҡарырға кәрәк. Был осраҡта $N$ — ябай һан булыуына өмөт барлыҡҡа килә, һәм уның ябайлығын ябайлыҡ тестары ярҙамында иҫбатларға тырышырға кәрәк.

Ябай һандар күмәклегенең сикһеҙлеге

Ябай һандар сикһеҙ күп. Был раҫлау боронғо грек математигы Евклид хөрмәтенә Евклид теоремаһы булараҡ иҫкә алына, сөнки был раҫлауҙың беренсе билдәле иҫбатланыуы уға ҡарай. Ябай һандарҙың сикһеҙлегенең тағы ла күп иҫбатлауҙары билдәле, шул иҫәптән Эйлерҙың аналитик иҫбатлауы, Гольдбахтың Ферма һандары нигеҙендә иҫбатлауы, Фурстенбергтың дөйөм топология ҡулланып иҫбатлауы һәм Куммерҙың элегант иҫбатлауы.

Билдәле иң ҙур ябай һан

Электән шул осорға билдәле иң ҙур ябай һандарҙы билдәләүсе яҙыуҙар алып барыла. Үҙ ваҡытында Эйлер, s|1=power|2|31 − 1 = 2 147 483 647 ябай һанын табып, рекордтарҙың береһен ҡуя.

Билдәле иң ҙур ябай һан 2019 йылдың ғинуарына ҡарата Мерсенн һаны M_82 589 933 = s|1=power|2|{{num|82589933 − 1. Ул 24 862 048 унарлы цифрҙан тора; был һан яҙылған китапта туғыҙ мең самаһы бит булыр ине. Уны 2018 йылдың 7 декабрендә, Мерсенн ябай һандарын таратылған эҙләү буйынса проект GIMPS сиктәрендә, табалар. Алдағы билдәле булған, 2017 йылдың декабрендә асылған иң ҙур ябай һан 1 612 623 тамғаға бәләкәйерәк була.

Мерсенн һандары ҡалғандарынан һөҙөмтәле ябайлыҡ тесы: Люк — Лемер тесы булыуы менән айырылып торалар. Шуның арҡаһында Мерсенн ябай һандары күптән билдәле иң ҙур ябай һандар булараҡ рекорд ҡуялар.

100 000 000 һәм 1 000 000 000-дан күберәк унарлы цифрҙан торған ябай һандарҙы тапҡан өсөн EFF ярашлы рәүештә 150 000 һәм 250 000 АҠШ долларына тигеҙ аҡсалата премия тәғәйенләй. Алдараҡ EFF 1 000 000 һәм 10 000 000 унарлы цифрҙан торған ябай һандарҙы тапҡан өсөн приздар тапшырған була.

Махсус күренештәге ябай һандар

Ябайлығы махсуслаштырылған алгоритмдар ҡулланып һөҙөмтәле асыҡланырға мөмкин булған күп кенә һандар бар.

• Мерсенн һандары — $M_{n}=2^{n}-1$ күренешендәге һандар, бында n — натураль һан. Шуның менән бергә Мерсенн һаны тик n — ябай һан булғанда ғына ябай булырға мөмкин. Юғарыла билдәләп киткәнсә, Люк — Лемер тесы һөҙөмтәле ябайлыҡ тесы булып тора.
• Ферма һандары — $F_{n}=2^{2^{n}}+1$ күренешендәге һандар, бында n — тиҫкәре булмаған бөтөн һан. Пепин тесы һөҙөмтәле ябайлыҡ тесы булып тора. 2015 йылдың февраленә ҡарата тик 5 Ферма ябай һаны билдәле (n = 0, 1, 2, 3, 4 өсөн), артабанғы егерме һигеҙ Ферма һаны ($F_{32}$-ны ла индереп, $F_{32}$-гә тиклем) ҡушма һан булып сыға, ләкин башҡа ябай Ферма һандары булмауы иҫбат ителмәгән.
• Вудал һандары — $W_{n}=n\cdot 2^{n}-1$ күренешендәге һандар. Люк — Лемер — Ризель тесы һөҙөмтәле ябайлыҡ тесы булып тора.
• Каллен һандары — $C_{n}=n\cdot 2^{n}+1$ күренешендәге һандар.
• Прот һандары — $P=k\cdot 2^{n}+1$ күренешендәге һандар, шуның менән бергә k таҡ һәм $2^{n}>k$. Прот һандары өсөн Бриллхарт — Лемер — Селфридж тесы (ингл. Brillhart–Lehmer–Selfridge test һөҙөмтәле ябайлыҡ тесы булып тора). Числа Каллена и числа Ферма являются частным случаем чисел Прота (соответственно при k = n и при k = 1, $n=2^{m}$).
• Миллс һандары — $P_{n}=[A^{3^{n}}]$ күренешендәге һандар, бында $A$ — Миллс константаһы.

Әлеге ваҡытта билдәләнгән типтарҙағы ябай һандарҙы табыу өсөн GIMPS, PrimeGrid, Ramsey@Home, Seventeen or Bust, Riesel Sieve, Wieferich@Home бүленгән иҫәпләү проекттары ҡулланыла.

Ҡайһы бер үҙсәнлектәре

• Әгәр p — ябай булһа, һәм ab p-ға бүленһә, ул саҡта a йәки b p-ға бүленә. Был фактты Евклид иҫбатлай һәм ул Евклид леммаһы булараҡ билдәле. Ул Арифметиканың төп теоремаһын иҫбатлағанда ҡулланыла.
• Алынмалар ҡулсаһы $\mathbb {Z} _{n}$ $n$ — ябай булғанда һәм тик шул саҡта ғына ялан була.
• Һәр яландың характеристикаһы — ноль йәки ябай һан.
• Әгәр $p$ — ябай, ә $a$ — натураль һан булһа, ул саҡта $a^{p}-a$ $p$-ға бүленә (Ферманың бәләкәй теоремаһы).
• Әгәр $G$ — тәртибе $|G|$ $p$-ға бүленгән сикле төркөм булһа, ул саҡта $G$ төркөмөнөң $p$ тәртибендәге элементы бар (Коши теоремаһы).
• Әгәр $G$ — сикле төркөм, һәм $p^{n}$ — $p$-ның $|G|$ бүленгән максималь дәрәжәһе булһа, ул саҡта $G$ төркөмөнөң $p^{n}$ тәртибендәге аҫтөркөмө бар, ул Силов аҫтөркөмө тип атала, етмәһә, Силов аҫтөркөмдәре һаны ниндәйҙер бөтөн $k$ өсөн $pk+1$-гә тигеҙ (Силов теоремаһы).
• Натураль $p>1$ һаны, әгәр $(p-1)!+1$ $p$-ға бүленһә, шул саҡта һәм бары шул саҡта ғына ябай була (Вильсон теоремаһы).
• Әгәр $n>1$ — натураль һан булһа, шундай $p$ ябай һаны бар, $n<p<2n$ (Бертран постулаты).
• Ябай һандарға кире һандар рәте таралыусан. Етмәһә, $x\to \infty$ өсөн

  $\sum _{p<x}{\frac {1}{p}}\ \sim \ \ln \ln x.$

• $a,a+q,a+2q,a+3q,...$ күренешендәге теләһә ниндәй арифметик прогрессияла, бында $a,q>1$ — бөтөн үҙ-ара ябай һандар, сикһеҙ күп ябай һандар бар (Арифметик прогрессияла ябай һандар тураһында Дирихле теоремаһы).
• 3-тән ҙурыраҡ теләһә ниндәй ябай һан $6k+1$ йәки $6k-1$ күренешендә күрһәтелә ала, бында $k$ — ниндәйҙер натураль һан. Бынан сығып, әгәр бер нисә эҙмә-эҙ килгән ябай һандарҙың айырмаһы (k>1 булғанда) бер төрлө булһа, ул һис шикһеҙ 6-ға бүленә — мәҫәлән: 251-257-263-269; 199-211-223; 20183-20201-20219.
• Әгәр $p>3$ — ябай булһа, ул саҡта $p^{2}-1$ 24-кә бүленә (шулай уҡ 3-кә бүленмәгән бөтә таҡ һандар өсөн дөрөҫ).
• Грин-Тао теоремаһы. Теләһә ниндәй оҙонлоҡтағы ябай һандарҙан торған арифметик прогрессиялар бар.
• Бер ниндәй ҙә ябай һан $n^{k}-1$ күренешендә була алмай, бында n>2, k>1. Икенсе төрлө әйткәндә, ябай һандан һуң килгән һан нигеҙе 2-нән ҙур булған квадрат йәки юғары дәрәжә була алмай. Бынан шулай уҡ, ябай һан $2^{k}-1$ күренешендә булһа, ул саҡта k — ябай һан булыуы килеп сыға (ҡарағыҙ. Мерсенн һандары).
• Бер ниндәй ҙә ябай һан $n^{2k+1}+1$ күренешендә була алмай, бында n>1, k>0. Икенсе төрлө әйткәндә, ябай һандың алдынан килгән һан нигеҙе 1-ҙән ҙур булған куб йәки юғарыраҡ таҡ күрһәткесле дәрәжә була алмай.
• Һәр ябай һанды (8n-1 күренешендәге һандарҙан башҡа) өс квадрат суммаһы рәүешендә күрһәтеп була.

Ҡулланылышы

Ябай һандар математиканың күп өлкәләрендә фундаменталь компоненттар булып торалар.

Арифметик функциялар

Арифметик функциялар, атап әйткәндә натураль һандар күмәклегендә билдәләнгән һәм комплекслы һандар күмәклегенән ҡиммәттәр ҡабул иткән функциялар, һандар теорияһында ҙур роль уйнайҙар. Айырым алғанда, улар араһында мультипликатив функциялар, йәғни түбәндәге үҙсәнлектәргә эйә булған $f$, функциялары иң мөһим булып торалар: әгәр $(a,b)$ пары үҙ-ара ябай һандарҙан торһа, ошо тигеҙлек дөрөҫ

$f(ab)=f(a)f(b)$

Мультипликатив функцияларҙың миҫалы булып Эйлер функцияһы $\phi$ тора, ул $n$ һанына количество натуральных чисел, меньших n-дан бәләкәй һәм уның менән үҙ-ара ябай натураль һандар күмәклеген һәм n һанының бүлеүселәре һанын ярашлы ҡуя. Был функцияның ябай һан дәрәжәһенән ҡиммәттәре:

• $\phi$ Эйлер Функцияһы:

$\phi (p^{m})=p^{m}-p^{m-1}$

• Бүлеүсе Функцияһы:

$\sigma (p^{m})=m+1$

Арифметик функцияларҙы, улар ябай һандар дәрәжәһе өсөн ҡабул иткән ҡиммәттәрҙе белгәндә, еңел иҫәпләп була. Ысынлап та n натураль һанының ҡабатлашыусыларға тарҡалмаһынан

$n=p_{1}^{q_{1}}\cdot ...\cdot p_{a}^{q_{a}}$

$f(n)=f(p_{1}^{q_{1}})\cdot ...\cdot f(p_{a}^{q_{a}})$ булыуын табабыҙ.

һәм ошонан сығып, $f(n)$-ды иҫәпләү мәсьәләһенә ҡайтҡанда, $f$-ты һәр ябай бүлеүсеһе дәрәжәһенән иҫәпләү $f$-ты дөйөм формула буйынса иҫәпләгәндән күпкә ябайыраҡ килеп сыға.

Мәҫәлән, Эйлер $\phi$ функцияһының n = 450 = 2 × 3 ² × 5 ² өсөн ҡиммәтен табыу өсөн,

$\phi (450)=\phi (2)\cdot \phi (3^{2})\cdot \phi (5^{2})=(2-1)\cdot (9-3)\cdot (25-5)=120$-ды иҫәпләү етә

Модулле арифметика

Модулле арифметикала ябай һандар ҙур роль уйнайҙар: $\mathbb {Z} /n\mathbb {Z}$ алынмалар ҡулсаһы, n ябай һан булғанда һәм тик шул саҡта ғына ялан була. Шулай уҡ $\mathbb {Z} /n\mathbb {Z}$ ҡулсаһының алынма тамырының булыуы ябай һандарға бәйле: ул n — ябай һан булғанда ғына бар, 1, 2, 4 йәки $p^{n}\circ 2p^{n}$ формаһындағы һан, бында p таҡ.

Модулле арифметиканың мөһим теоремаларының береһе булып Ферманың бәләкәй теоремаһы тора. Был теорема, теләһә ниндәй р ябай һаны һәм теләһә ниндәй натураль a һаны өсөн:

$a^{p}\equiv a{\pmod {p}}$ тип раҫлай

йәки теләһә ниндәй р ябай һаны һәм р-ға бүленмәгән теләһә ниндәй натураль а өсөн:

$a^{p-1}\equiv 1{\pmod {p}}$ дөрөҫ.

Был үҙсәнлекте һан ябай түгел икәнен тикшереү өсөн ҡулланырға мөмкин. Ысынлап та, әгәр n ниндәйҙер натураль а өсөн:

$a^{n}\not \equiv a{\pmod {n}}$ булһа,

ул саҡта n ябай була алмай. Ләкин был үҙсәнлек һанды ябайлыҡҡа тикшереү өсөн ҡулланыла алмай: Кармайкл һандары тип аталған шундай һандар бар (иң бәләкәйе — 561), улар өсөн был дөрөҫ түгел. Кармайкл һаны тип n менән үҙ-ара ябай булған һәр b нигеҙе буйынса ялған ябай һан булған ҡушма һан атала. 1994 йылда Уильям Роберт Альфорд, Эндрю Гранвиль һәм Померанс Карл бындай һандарҙың сикһеҙ күп булыуын күрһәтәләр.

Төркөмдәр теорияһы

Ябай һандар шулай уҡ алгебрала төп ролде уйнайҙар. Төркөмдәр теорияһында һәр элементы р ябай һанының дәрәжәһе булған төркөм P-төркөм тип атала. P-төркөм, төркөмдөң тәртибе (уның элементтарының һаны) р-ның дәрәжәһе булғанда һәм бары шул саҡта ғына сикле була. Прюферҙың p-төркөмө сикһеҙ р-төркөмдөң миҫалы булып тора. p-төркөмө тривиаль булмаған үҙәккә эйә булыуы билдәле, тимәк, ябай була алмайҙар (p элементтары булған төркөмдән башҡа); әгәр төркөм сикле булһа, бынан тыш, бөтә нормаль аҫтөркөмдәр үҙәкте тривиаль булмаған рәүештә киҫәләр. Ябай һандың модуле буйынса ҡабатлауҙың цикллы төркөмө бындай төркөмдәрҙең миҫалы булып тора.

p тәртибендәге бөтә төркөмдәр цикллы булалар һәм шуға күрә Абель төркөмө булалар; шулай уҡ һәр p ² тәртибендәге төркөм Абель төркөмө була. Бынан тыш, һәр сикле Абель төркөмө сикле һандағы цикллы р-төркөмдәрҙең тура ҡабатландығына изоморфлы.

Коши теоремаһында, что әгәр сикле G төркөмөнөң тәртибе p ябай һанына бүленһә, G төркөмөнә p тәртибендәге элементтар инә. Был теорема Силов теоремаларында дөйөмләштерелә.

Асыҡ асҡыслы криптосистема

Асыҡ асҡыслы криптосистемаларҙың RSA һәм Диффи-Хеллман асҡыстары менән алмашыныу кеүек ҡайһы бер алгоритмдары, ҙур ябай һандарға (ғәҙәттә 1024—2048 бит) нигеҙләнгәндәр. RSA, ике (ҙур) x һәм y һандарын ҡабатлауҙы башҡарыу, әгәр уларҙың $x\cdot y$ ҡабатландығы ғына билдәле булһа, x һәм y үҙ-ара ябай һандарын иҫәпләүгә ҡарағанда күпкә ябайыраҡ (йәғни һөҙөмтәле) тигән фаразға таяна. Диффи-Хеллман асҡыстары менән алмашыныу модуле буйынса дәрәжәгә күтәреүҙең һөҙөмтәле алгоритмдары булыуына таяна, ә кире операция — Дискретлы логарифмлау ҡатмарлы тип һанала.

RSA

Ҙур һандарҙы факторизациялау беренсе һөҙөмтәле RSA — асыҡ асҡыслы криптография ысулын эшләүгә килтерә. Был криптографик системала, шифрланған хәбәр алырға тейеш булған кеше, асҡыс генерирлай: бирелгән үлсәмдәге (ғәҙәттә, 1024- йәки 2048-битлы һандар ҡулланыла) төрлө ике $p$ һәм $q$ осраҡлы ябай һандары һайлап алына. Артабан уларҙың модуль тип аталған $n=p*q$ ҡабатландығы иҫәпләнә. Эйлер функцияһының $n$ һанынан ҡиммәте иҫәпләнә: $\phi (n)=(p-1)(q-1)$. $\phi (n)$ функцияһының ҡиммәте менән үҙ-ара ябай $e$ ($1<e<\phi (n)$) бөтөн һаны һайлап алына. Ғәҙәттә $e$ сифатында ҙур булмаған ябай һанды алалар (мәҫәлән, ябай Ферма һандары). $e$ һаны асыҡ экспонента(ингл. public exponent) тип атала. Серле экспонента тип аталған, e һанына $\phi (n)$ модуле буйынса мультипликатив кире $d$ һанын иҫәпләйҙәр. RSA-ның асыҡ асҡысы (ингл. RSA public key) сифатында $\{e,n\}$ һандар пары яҙыла. $\{d,\phi (n)\}$ пары RSA-ның бикле асҡысы (ингл. RSA private key) ролен уйнай һәм сер итеп һаҡлана.

Теоретик бикле асҡысты асыҡтан-асыҡ булған мәғлүмәттән алырға мөмкин: хәҙерге ваҡытта бының өсөн $n$ һанын факторизациялау талап ителә, әгәр ябай һандар билдәле шарттарҙы ҡәнәғәтләндерһәләр һәм «етерлек ҙур» булһалар, был һаҡланыусы хәбәрҙе ебәреүҙе хәүефһеҙ итә. Хәбәрҙең шифрын сисеү өсөн $n$ һанын факторизациялауға тура атака менән бәйле булмаған һөҙөмтәле ысулдар бармы икәне әлегә билдәһеҙ, ләкин асыҡ асҡысты насар һайлау бындай атакалар өсөн системаны йомшаҡ (ныҡлы түгел) итә.Ҡалып:Source-ref

1991 йылда RSA Security ярым ябай һандар теҙмәһен баҫтырып сығара, ысулдың хәүефһеҙлеген раҫлау һәм был өлкәлә тикшеренеүҙәрҙе дәртләндереү маҡсатында, уларҙың ҡайһы берҙәрен ҡабатлашыусыларға тарҡатыу өсөн аҡсалата приз тәҡдим итә: инициатива Challenge RSA Factoring тип атала. Күп йылдар дауамында был һандарҙың ҡайһы берҙәре ҡабатлашыусыларға тарҡатыла,ә ҡалғандары өсөн факторизация проблемаһы асыҡ ҡала; ләкин конкурс 2007 йылда тамамлана.

Ябай һандарҙы табыу өсөн формулалар

Төрлө ваҡыттарҙа, уға ингән үҙгәреүсәндәрҙең төрлө ҡиммәттәрендә, ҡиммәте ябай һан булған аңлатма табырға маташыуҙар була. Л. Эйлер, n = 0, 1, 2, …, 40 булғанда ябай ҡиммәттәр ҡабул иткән, $\textstyle n^{2}-n+41$ күпбыуынын тәҡдим итә. Ләкин n = 41 булғанда күпбыуындың ҡиммәте ҡушма һан була. n-дың бөтә бөтөн ҡиммәттәрендә лә ҡиммәте ябай һан булған бер n үҙгәреүсәнле күпбыуын булмауын иҫбат итергә мөмкин . П. Ферма бөтә [[Ферма һандары|Ҡалып:Power + 1]] күренешендәге һандар]] ябай тип фараз итә; ләкин Эйлер был гипотезаны кире ҡаға, ул Ҡалып:Power + 1 = 4 294 967 297 һаны — ҡушма булыуын иҫбатлай.

Шулай булыуға ҡарамаҫтан, үҙгәреүсәндәрҙең тиҫкәре булмаған ҡиммәттәрендә ыңғай ҡиммәттәре күмәклеге ябай һандар күмәклеге менән тап килгән күмәклектәр бар. 26 үҙгәреүсәндән торған һәм 25 дәрәжәләге күпбыуын шулаҙың бер миҫалы булып тора

${\begin{aligned}{\bigl (}k+2{\bigr )}{\bigl \{}1&-{\bigl [}wz+h+j-q{\bigr ]}^{2}-{\bigl [}(gk+2g+k+1)(h+j)+h-z{\bigr ]}^{2}-{\bigl [}2n+p+q+z-e{\bigr ]}^{2}\\&-{\bigl [}16(k+1)^{3}(k+2)(n+1)^{2}+1-f^{2}{\bigr ]}^{2}-{\bigl [}e^{3}(e+2)(a+1)^{2}+1-o^{2}{\bigr ]}^{2}-{\bigl [}(a^{2}-1)y^{2}+1-x^{2}{\bigr ]}^{2}\\&-{\bigl [}16r^{2}y^{4}(a^{2}-1)+1-u^{2}{\bigr ]}^{2}-{\bigl [}((a+u^{2}(u^{2}-a))^{2}-1)(n+4dy)^{2}+1-(x+cu)^{2}{\bigr ]}^{2}-{\bigl [}n+l+v-y{\bigr ]}^{2}\\&-{\bigl [}(a^{2}-1)l^{2}+1-m^{2}{\bigr ]}^{2}-{\bigl [}ai+k+1-l-i{\bigr ]}^{2}-{\bigl [}p+l(a-n-1)+b(2an+2a-n^{2}-2n-2)-m{\bigr ]}^{2}\\&-{\bigl [}q+y(a-p-1)+s(2ap+2a-p^{2}-2p-2)-x{\bigr ]}^{2}-{\bigl [}z+pl(a-p)+t(2ap-p^{2}-1)-pm{\bigr ]}^{2}{\bigr \}}\end{aligned}}$

Шундай типтағы 42 үҙгәреүсәнле күпбыуындарҙың иң бәләкәй дәрәжәһе — 5; дәрәжәһе яҡынса 1,6•10⁴⁵ булғанда үҙгәреүсәндәрҙең иң бәләкәй һаны — 10. Был һөҙөмтә Матиясевич Юрий Владимирович иҫбатлаған теләһә ниндәй һанап сыҡмалы күмәклектең диофантлы булыуының айырым осрағы булып тора.

Шуныһы ҡыҙыҡ, юғарыла килтерелгән ябай һандарҙы тыуҙырыусы күпбыуын үҙе ҡабатлашыусыларға тарҡала. Был күпбыуындың икенсе ҡабатлашыусыһы (фигуралы йәйә эсендә) бер минус квадраттар суммаһы күренешендә. Шулай итеп күпбыуын, (ыңғай $k$ булғанда) квадраттарҙың һәр береһе (йәғни квадрат йәйәләрҙәге һәр күпбыуын) нулгә тигеҙ булғанда ғына ыңғай ҡиммәттәр ҡабул итә ала. Был осраҡта фигуралы йәйәләрҙәге аңлатма 1-гә тигеҙ була.

Асыҡ мәсьәләләр

Ябай һандарҙың бүленеше p_n = f (Δs_n); Δs_n = p_n+1² — p_n². Δp_n = p_n+1 — p_n; Δp_n = 2, 4, 6, … .

Ошоға тиклем ябай һандарға ҡарата күп асыҡ мәсьәләләр бар, уларҙың иң билдәлеләрен Ландау Эдмунд 1912 йылда Бишенсе Халыҡ-ара математик конгреста һынап китә:

1. Гольдбах проблемаһы (беренсе Ландау проблемаһы): икенән ҙур булған һәр йоп һанды ике ябай һандың суммаһы рәүешендә күрһәтеп була тип әйтеү дөрөҫмө?
2. Ландауҙың икенсе проблемаһы: «ябай игеҙәктәр» — айырмаһы икегә тигеҙ булған ябай һандар парҙары күмәклеге сикһеҙме? 2013 йылда Нью-Гэмпшира университеты математигы Чжан Итан, араларындағы алыҫлығы 70 миллиондан артмаған сикһеҙ ҙур һандағы ябай һандар парҙары бар икәнен иҫбатлай. Һуңғараҡ, Мейнард Джеймс һөҙөмтәне 600-гә тиклем яҡшырта. 2014 йылда Тао Теренс етәкселегендә Polymath проекты, алыҫлыҡ баһаһын 246-ға алмаштырып, һуңғы ысулды бер аҙ яҡшырталар.
3. Лежандр гипотезаһы (Ландауҙың өсөнсө проблемаһы): һәр натураль $n$ һаны өсөн $n^{2}$ һәм $(n+1)^{2}$ араһында һәр ваҡытта ябай һан табыла тип раҫлау дөрөҫмө?
4. Ландауҙың дүртенсе проблемаһы: $n^{2}+1$ күренешендәге ябай һандар күмәклеге сикһеҙме, бында $n$ — натураль һан?

Шулай уҡ күп бөтөн һанлы эҙмә-эҙлектәрҙә, Мерсенн һандарын, Фибоначчи һандарын, Ферма һандарын һәм башҡаларҙы ла индереп, сикһеҙ һандағы ябай һандарҙың булыуы ла асыҡ проблема булып ҡала.

Вариациялар һәм дөйөмләштереүҙәр

Килтереп булмай торған һәм ябай элементтар

Мәҡәләнең башында ябай һан билдәләмәһе бирелгәйне: ике генә бүлеүсеһе — берәмек һәм һан үҙе булған натураль һан ябай һан тип атала. Оҡшаш төшөнсәләрҙе башҡа алгебраик структураларҙа ла индерергә мөмкин; йышыраҡ нулдең бүлеүселәренән башҡа коммутатив ҡулсалар ҡаралалар (бөтөнлөк өлкәләре). Ләкин бындай ҡулсаларҙың мультипликатив төркөм төҙөүсе берәмектең бүлеүселәре булырға мөмкин. Мәҫәлән, бөтөн һандар ҡулсаһында берәмектең ике бүлеүсеһе бар: $+1$ һәм $-1.$ Шуға күрә берәмектең бүлеүселәренән башҡа бөтә бөтөн һандарҙыңике түгел, ә кәмендә дүрт бүлеүсеһе була; мәҫәлән, 7 һанының бүлеүселәре $1;7;-1;-7.$ Был дөйөмләштерелгән ябай һан төшөнсәһе уның икенсе үҙсәнлектәренә нигеҙләнергә тейеш булыуын аңлата.

Бөтөнлөк өлкәһе өсөн килтереп булмай торған элемент ябай һандың аналогы булып тора, ул ошолай билдәләнә.

Бөтөнлөк өлкәһенең нулдән айырмалы $p$ элементы, әгәр ул берәмектең бүлеүсеһе булмаһа һәм $p=ab$ тигеҙлегенән $a$ йәки $b$ берәмектең бүлеүсеһе була икәне килеп сыҡһа, килтереп булмай торған (ҡайһы берҙә тарҡатып булмай торған) тип атала.

Был билдәләмә бөтөн һандар өсөн ябай натураль һандар, шулай уҡ уларға ҡапма-ҡаршы һандар килтереп булмай торған элементтар булыуын аңлата.

Билдәләмәнән, килтереп булмай торған $p$ элементының бүлеүселәре күмәклеге ике өлөштән: берәмектең бөтә бүлеүселәренән һәм $p$-ның берәмектең бөтә бүлеүселәренә ҡабатландыҡтарынан (был ҡабатландыҡтар $p$ злементтар менән ассоциирлаштырылған тип аталалар) тороуы килеп сыға. Йәғни, килтереп булмай торған $p$-ның бүлеүселәре һаны, әгәр ул сикле булһа, ҡулсала берәмектең бүлеүселәре һанынан ике тапҡыр күп.

Арифметиканың төп теоремаһы аналогы ҙур әһәмиәткә эйә, ул дөйөмләштерелгән рәүештә ошолай әйтелә:

Ҡулса, әгәр унда берәмектең бүлеүсеһе булмаған һәр нулдән айырмалы элемент килтереп булмай торған элементтарҙың ҡабатландығы рәүешендә күрһәтелә алһа, шуның менән бергә был күрһәтеү ҡабатлашыусыларҙың алмаштырмаһына һәм уларҙың ассоциирлаштырылғанына (берәмектең бүлеүселәренә ҡабатландығына) тиклем аныҡлыҡ менән берҙән-бер булһа, факториаль тип атала.

Теләһә ниндәй бөтөнлөк өлкәһе лә факториаль түгел, ҡарағыҙ. контрмиҫал. Евклид ҡулсаһы һәр ваҡыт факториаль.

Ябай һан төшөнсәһенең башҡа, ябай элемент тип аталған тарыраҡ дөйөмләштереүе бар.

Бөтөнлөк өлкәһенең нулдән айырмалы $p$ элементы, әгәр ул берәмектең бүлеүсеһе булмаһа һәм $ab$ ҡабатландығы $p$-ға, $a$ йәки $b$ элементтарының береһе генә булһа ла $p$-ға бүленгән осраҡта ғына бүленә алһа, ябай тип атала.

Ябай элемент һәр ваҡыт килтереп булмай торған. Ысынлап та, әгәр $p$ элементы ябай һәм $p=ab$ булһа, ябай элемент билдәләмәһе буйынса ҡабатлашыусыларҙың береһе, $a$ булһын әйҙә, $p$-ға бүленә, йәғни $a=pq.$ Ул саҡта $p=ab=pqb$ йәки, $p$-ға ҡыҫҡартып (бөтөнлөк өлкәһендә нулдән айырмалы ҡабатлашыусыны ҡыҫҡартыу һәр саҡ мөмкин): $1=qb,$ йәғни $b$ берәмектең бүлеүсеһе була. Ҡалып:Шииһ

Киреһе, дөйөм алғанда, дөрөҫ түгел, килтереп булмай торған элемент, әгәр ҡулса факториаль булмаһа, ябай була алмай. Миҫал: $a+b{\sqrt {5}}i$ күренешендәге һандар ҡулсаһын ҡарайыҡ, бында $a,b$ — бөтөн һандар. 3 һаны унда килтереп булмай торған һан, сөнки уның тик 4 бүлеүсеһе бар: $3,1,-3,-1$. Ләкин ул ябай элемент түгел, быға ошо тигеҙлек ышандыра:

$\left(2+{\sqrt {5}}i\right)\left(2-{\sqrt {5}}i\right)=9$

Тигеҙлектең уң яғы 3-кә бүленә, ләкин бер ҡабатлашыусы ла 3-кә бүленмәй. Был факттан ҡаралған ҡулсаның факториаль булмауы тураһында һығымта яһап була; ысынлап та, $6=2\cdot 3=(1-i{\sqrt {5}})(1+i{\sqrt {5}})$ тигеҙлеге был ҡулсала килтереп булмай торған ҡабатлашыусыларға тарҡатыу берҙән бер түгел булыуын күрһәтә.

Миҫалдар

Бөтөн һандар ҡулсаһы факториаль. Унда, юғарыла телгә алынғанса, берәмектең ике бүлеүсеһе.

Гаусс бөтөн һандары

Гаусс һандары ҡулсаһы $a+bi$ күренешендәге, бында $a,b$ — бөтөн һандар, комплекслы һандарҙан тора. Берәмектең бүлеүселәре дүртәү: $1;-1;i;-i.$ Был ҡулса факториаль, ғәҙәттәге ябай һандарҙың бер өлөшө һәм «ябай гаусс һандары» килтереп булмай торған элементтар булып торалар (мәҫәлән, $1+i$). Ҡарағыҙ. Гаусс һандары ябайлығы критерийы.

Гаусс һандары ҡулсаһында ябай булмаған 2 һаны өсөн ҡабатлашыусыларға тарҡатыу миҫалы: $2=(1+i)(1-i)=i(1-i)(1-i)$ — бында тарҡатыу берҙән бер түгел һымаҡ күренә генә, сөнки $1-i=(-i)(1+i)$ тигеҙлегенә ярашлы, $1-i$ $1+i$ менән ассоциациялана.

Эйзенштейндың бөтөн һандары

Эйзенштейндың бөтөн һандары ҡулсаһы $\mathbb {Z} [\omega ]$ түбәндәге күренештәге комплекслы һандарҙан тора:

$z=a+b\omega ,$ бында $a,b$ — бөтөн һандар, $\omega ={\frac {1}{2}}(-1+i{\sqrt {3}})=e^{2\pi i/3}$ (берәмектең куб тамыры),

Был ҡулсала берәмектең алты бүлеүсеһе бар: (±1, ±ω, ±ω²), ул Евклид ҡулсаһы һәм шуға күрә факториаль. Ҡулсаның килтереп булмай торған элементтары (улар шулай уҡ ябай элементтар) Эйзенштейндың ябай һандары тип аталалар.

Ябайлыҡ критерийы: Эйзенштейндың бөтөн һаны $z=a+b\omega$, түбәндәге бер-береһен кире ҡағыусы шарттарҙың береһе үтәлгәндә һәм шул саҡта ғына Эйзенштейндың ябай һаны була:

1. $z$ $3n-1$ күренешендәге натураль ябай һан менән ассоциацияланғанда
2. $|z|^{2}=a^{2}-ab+b^{2}$ ($z$-тың нормаһы) $3n$ йәки $3n+1$ күренешендәге натураль ябай һан булһа.

Бынан Эйзенштейндың теләһә ниндәй бөтөн һанының нормаһы йә ябай натураль һан, йә ябай натураль һандың квадраты була икәне килеп сыға.

Эйзенштейндың ябай һандары менән ассоциацияланған йәки комплекслы-эйәртеүле һандар, шулай уҡ Эйзенштейндың ябай һандары булалар.

Күпбыуындар ҡулсаһы

Алгебрала ниндәйҙер $K$ ҡулсаһынан алынған коэффициентлы күпбыуындарҙан торған $K[x]$ күпбыуындар ҡулсаһы ҙур әһәмиәткә эйә. Бында берәмектең бүлеүселәре булып нулдән айырмалы константалар (нуленсе дәрәжә күпбыуындар булараҡ) торалар. Күпбыуындар ҡулсаһы евклидово һәм шуға күрә факториаль. Әгәр $K$ сифатында ысын һандар яланын алғанда, бөтә 1-се дәрәжә күпбыуындар һәм ысын тамырҙары булмаған 2-се дәрәжә күпбыуындар (йәғни уларҙың дискриминанты тиҫкәре), килтереп булмай торған күпбыуындар булалар.

Шулай уҡ ҡарағыҙ

• Незаконное простое число
• Суперпростое число
• Полупростое число
• Примориал
• Простые числа, отличающиеся на шесть
• Случайное простое число
• Составное число
• Список простых чисел
• Уникальное простое

Әҙәбиәт

• Ван дер Варден. Алгебра. Определения, теоремы, формулы. — СПб.: Лань, 2004. — 624 с. — ISBN 5-8114-0552-9.
• Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М.: МЦНМО, 2003. — 328 с. — ISBN 5-94057-103-4. Архивная копия от 27 ғинуар 2007 на Wayback Machine
• Винберг Э. Б. Малая теорема Ферма и ее обобщения (урыҫ) // Матем. просв. — М.: Изд-во МЦНМО, 2008. — Т. 12. — С. 43—53.
• Гальперин Г. Просто о простых числах // Квант. — № 4. — С. 9—14,38.
• Генри С. Уоррен, мл. Глава 16. Формулы для простых чисел // Алгоритмические трюки для программистов = Hacker's Delight. — М.: «Вильямс», 2007. — 288 с. — ISBN 0-201-91465-4.
• Карпушина Н. Палиндромы и «перевёртыши» среди простых чисел (рус.) // Наука и жизнь. — 2010. — № 5.
• Кордемский Б. А. Математическая смекалка. — М.: ГИФМЛ, 1958. — 576 с.
• Кормен Т., Лейзер Ч. Глава 33.8. Проверка чисел на простоту // Алгоритмы. Построение и анализ. — М.: МЦНМО, 2002. — С. 765—772. — ISBN 5-900916-37-5.
• Крэндалл Р., Померанс К. Простые числа. Криптографические и вычислительные аспекты = Prime Numbers: A Computational Perspective. — М.: УРСС, Либроком, 2011. — 664 с. — ISBN 978-5-397-02060-2.
• Курош А. Г. . Лекции по общей алгебре. — 2-е изд.. — Наука, 1973.
• Ленг С. Алгебра. — М.: Мир, 1967.
• Матиясевич Ю.. Формулы для простых чисел // Квант. — 1975. — № 5. — С. 5—13.
• Нестеренко Ю. В. Алгоритмические проблемы теории чисел // Введение в криптографию / Под редакцией В. В. Ященко. — Питер, 2001. — 288 с. — ISBN 5-318-00443-1.
• Простое число // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — 352 с.
• Энрике Грасиан. Простые числа. Долгая дорога к бесконечности. — Де Агостини, 2014. — Т. 3. — 148 с. — (Мир математики). — ISBN 978-5-9774-0682-6. — ISBN 978-5-9774-0637-6.
• Bakhtiari M., Maarof M. A. Serious Security Weakness in RSA Cryptosystem (ингл.) // IJCSI — 2012. — Vol. 9, Iss. 1, No 3. — P. 175—178. — ISSN 1694-0814; 1694-0784
• Crandall R., Pomerance C. Глава 3. «Recognizing Primes and Composites». Глава 4. «Primality Proving» // Prime Numbers: A Computational Perspective. — Springer, 2005. — С. 117—224. — ISBN 0-387-25282-7.

Һылтанмалар

• Кноп К. В погоне за простотой.
• The Prime Pages (инг.) — база данных наибольших известных простых чисел (инг.).
• Геометрия простых и совершенных чисел (исп.).
• Скрипт визуализации
• Форум искателей простых чисел (инг.).