Өс үлсәмле арауыҡ
| Өс үлсәмле арауыҡ | |
 | |
| Ҡыҫҡаса атамаһы | 3D[1] |
|---|---|
| Алдағы | ике үлсәмле арауыҡ |
| Тәртип буйынса һуңыраҡ килеүсе | дүрт үлсәмле арауыҡ[d] |
| Ҡайҙа өйрәнелә | стереометрия[d] |
| Вики-проект | Проект:Математика[d] |

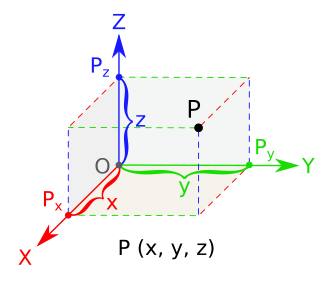
Өс үлсәмле арауыҡ — беҙ йәшәгән материаль донъяның геометрик моделе. Был Евклид арауығы өс үлсәмле тип атала, сөнки уның өс бер төрлө үлсәме — бейеклеге, киңлеге һәм оҙонлоғо бар, йәғни өс үлсәмле арауыҡ өс ортогональ берәмек вектор менән бирелә.
Өс үлсәмле арауыҡты аңлау кешелә сабый сағында үҫешә тип иҫәпләнә, һәм кешенең хәрәкәттәге үҙ-ара ярашыуы менән тығыҙ бәйләнгән. Солғап алған донъяны өс үлсәмдә һиҙеү органдары менән визуаль ҡабул итеү һәләте тәрәнлекте тойоу тип атала. Аналитик геометрияла өс үлсәмле арауыҡтың һәр нөктәһе өс дәүмәл — координаталар йыйылмаһы кеүек һүрәтләнә. Координаталар башында киҫешкән өс үҙ-ара перпендикуляр координаталар күсәре бирелә. Нөктәнең урыны ошо өс күсәргә ҡарата тәртипкә килтерелгән өс һан менән бирелә. Был һандарҙың һәр береһе ярашлы күсәр буйлап үлсәнгән иҫәпләү башынан нөктәгә тиклемге алыҫлыҡты бирә, был нөктәнән ҡалған ике күсәр менән яһалған яҫылыҡҡа тиклем алыҫлыҡҡа тигеҙ. Шулай уҡ башҡа координаталар системаһы бар, йышыраҡ цилиндрик һәм сферик системалар ҡулланыла.
Һыҙыҡлы алгебра икенсе төрлө ҡараш бирә, унда һыҙыҡлы бәйһеҙлек төшөнсәһе мөһим роль уйнай. Ҡумтаның бейеклеге уның оҙонлоғона һәм киңлегенә бәйле түгел, шул сәбәпле арауыҡ өс үлсәмле. Һыҙыҡлы алгебра телендә арауыҡ өс үлсәмле, сөнки һәр нөктә өс һыҙыҡлы бәйһеҙ векторҙар комбинацияһы менән бирелергә мөмкин. Был терминдарҙа арауыҡ-ваҡыт дүрт үлсәмле, сөнки нөктәнең ваҡыт арауығындағы урыны уның арауыҡтағы урынына бәйле түгел.
Өс үлсәмле арауыҡтың бер нисә үҙсәнлеге бар, улар уны башҡа үлсәмле арауыҡтарҙан айырып торалар. Мәҫәлән, был арҡан киҫәгендә төйөндәр бәйләп булған иң бәләкәй үлсәмле арауыҡ[2]. Физиканың күп закондары, мәҫәлән кире квадраттарҙың күп закондары беҙҙең арауыҡтың өс үлсәмле булыуы менән бәйле[3].
Нуль үлсәмле, бер үлсәмле һәм ике үлсәмле арауыҡтарҙы өс үлсәмле арауыҡта урынлашыусылар кеүек ҡарарға мөмкин; ул үҙе дүрт үлсәмле арауыҡ моделенең өлөшө тип иҫәпләнергә мөмкин (ҡайһы берҙә дүртенсе үлсәм тип ваҡытты иҫәпләйҙәр)[4].
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ https://dicosigles.fr/
- ↑ Dale Rolfsen, Knots and Links, Publish or Perish, Berkeley, 1976, ISBN 0-914098-16-0
- ↑ Brian Greene, The Fabric of the Cosmos, Random House, New York, 2003, ISBN 0-375-72720-5
- ↑ Четырёхмерное пространство — время. Дата обращения: 26 февраль 2009. Архивировано 18 февраль 2011 года.
