Рациональ һан

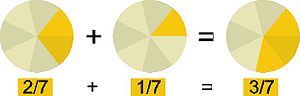
Рациональ һан (лат. ratio — сағыштырма, бүлеү, кәсер) — ябай кәсер ${\frac {m}{n}}$ рәүешендә күрһәтергә мөмкин булған һан, числитель $m$ — бөтөн һан, ә знаменатель $n$ — натураль һан, миҫалға 2/3. Кәсер төшөнсәһе бер нисә мең йыл элек барлыҡҡа килгән, ҡайһы бер дәүмәлдәрҙе (оҙонлоҡ, ауырлыҡ, майҙан һ.б.) үлсәү кәрәклеге килеп тыуғас, кешеләр бөтөн һандар ғына етмәүен һәм өлөш төшөнсәһе индереү кәрәклеген аңлай: ярты, өсөнсө өлөш һ.б. Кәсерҙәр һәм улар өҫтөндә ғәмәлдәр менән, мәҫәлән, шумерҙар, боронғо египетлылар һәм гректар файҙаланғандар.

Рациональ һандар күмәклеге

Рациональ һандар күмәклеге $\mathbb {Q}$ (ингл. quotient «бүлендек» һүҙенән) менән тамғалана һәм түбәндәге күренештә яҙылырға мөмкин:

\mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,n\in \mathbb {N} ^{+}\right\}.

Икенсе төрлө әйткәндә, числителдең (m) тамғаһы булырға мөмкин, ә знаменатель (n) ыңғай бөтөн һан булырға тейеш.

Шуның менән бергә, бер үк кәсерҙең төрлө яҙылышы булырға мөмкин, мәҫәлән, ${\frac {3}{4}}$ һәм ${\frac {9}{12}}$ , (бер береһенән числителен дә һәм знаменателен дә бер үк натураль һанға ҡабатлап йәки бүлеп табырға мөмкин булған бөтә кәсерҙәр). Кәсерҙең числителен һәм знаменателен уларҙың иң ҙур уртаҡ бүлеүсеһенә бүлеп, рациональ һандың берҙән-бер ҡыҫҡармай торған күренештәге кәсерен табырға мөмкин булғанлыҡтан, рациональ һандар күмәклеге тураһында үҙ-ара ябай бөтөн числителле һәм натураль знаменателле ҡыҫҡармай торған кәсерҙәр күмәклеге һымаҡ һөйләргә мөмкин:

\mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,n\in \mathbb {N} ^{+}\gcd(m,n)=1\right\}.

Бында $\gcd(m,n)$ — $m$ һәм $n$ -дың иң ҙур уртаҡ бүлеүсеһе.

Рациональ һандар күмәклеге бөтөн һандар күмәклегенең тәбиғи дөйөмләшеүе булып тора. Күренеүенсә, әгәр рациональ һандың $a={\frac {m}{n}}$ знаменателе $n=1$ булһа, ул саҡта $a=m$ бөтөн һан була.

Рациональ һандар күмәклеге һанлы күсәрҙә бөтә урында тығыҙ урынлашҡан: теләһә ниндәй төрлө ике рациональ һан араһында бер булһа ла рациональ һан урынлашҡан (тимәк, сикһеҙ күп рациональ һандар). Шулай булыуға ҡарамаҫтан, асыҡланыуынса, рациональ һандар күмәклеге иҫәпләмә ҡеүәтле (йәғни уның бөтә элементтарын да нумерлап сығырға мөмкин). Боронғо гректар осоронан кәсер рәүешендә күрһәтеп булмаған һандар барлығы билдәле: улар квадраты икегә тигеҙ булған рациональ һан булмауын иҫбат иткәндәр. Бөтә дәүмәлдәрҙе лә күрһәтеү өсөн рациональ һандарҙың етешмәүе артабан ысын һандар төшөнсәһенә килтерә. Ысын һандар күмәклеге (бер үлсәмле арауыҡҡа ярашлы булған) төшөнсәһенән айырмалы рәүештә, рациональ һандар күмәклеге нуль үлсәмле.

Терминология

=== Формаль бил also|Бүлендектәр ҡулсаһы}} Формаль рәүештә рациональ һандарға парҙар эквивалентлығы кластары күмәклеге булараҡ билдәләмә бирелә $\left\{(m,\;n)\mid m\in \mathbb {Z} ,\;n\in \mathbb {N} ^{+}\right\}$ эквивалентлыҡ бәйләнеше буйынса $(m,\;n)\sim (m',\;n')$ , әгәр $m\cdot n'=m'\cdot n$ . Шуның менән бергә ҡушыу һәм ҡабатлау ғәмәлдәре түбәндәгесә билдәләнә:

$\left(m_{1},\;n_{1}\right)+\left(m_{2},\;n_{2}\right)=\left(m_{1}\cdot n_{2}+m_{2}\cdot n_{1},\;n_{1}\cdot n_{2}\right);$
$\left(m_{1},\;n_{1}\right)\cdot \left(m_{2},\;n_{2}\right)=\left(m_{1}\cdot m_{2},\;n_{1}\cdot n_{2}\right).$

Бәйле билдәләмәләр

Шулай уҡ ҡарағыҙ: Кәсер (математика)

Дөрөҫ, дөрөҫ булмаған һәм ҡатнаш кәсерҙәр

Кәсер дөрөҫ кәсер тип атала, әгәр числителдең модуле знаменателдең модуленән бәләкәйерәк булһа. Дөрөҫ кәсерҙәр модуле буйынса берҙән бәләкәйерәк рациональ һандар булып торалар. Әгәр кәсер дөрөҫ кәсер булмаһа, дөрөҫ булмаған кәсер тип атала һәм модуле буйынса бергә тигеҙ йәки ҙурыраҡ булған рациональ һанды күрһәтә.

Ҡатнаш кәсер тип аталған дөрөҫ булмаған кәсерҙе бөтөн һандың һәм дөрөҫ кәсерҙең суммаһы рәүешендә күрһәтергә мөмкин. Мәҫәлән, $2{\frac {3}{7}}=2+{\frac {3}{7}}={\frac {14}{7}}+{\frac {3}{7}}={\frac {17}{7}}$ . Ошондай яҙыу (төшөрөп ҡалдырылған ҡушыу тамғаһы менән) элементар арифметикала ҡулланылһа ла, аралаш һандың яҙылышы бөтөн һанды кәсергә ҡабатлау тамғаланышы менән оҡшаш булғанлыҡтан, ҡәтғи математик әҙәбиәттә был яҙыуҙы ҡулланыуҙан тыйылалар.

Кәсер бейеклеге

Ябай кәсерҙең бейеклеге — был кәсерҙең числителе модуленең һәм знаменателенең суммаһы. Рациональ һандың бейеклеге — был һанға ярашлы ҡыҫҡармай торған ябай кәсерҙең числителе модуленең һәм знаменателенең суммаһы.

Мәҫәлән, $-{\frac {15}{6}}$ кәсеренең бейеклеген табыу өсөн башта унан ҡыҫҡармай торған кәсерҙе табырға кәрәк. Ҡыҫҡармай торған кәсер ошолай күренештә: $-{\frac {5}{2}}$ . Аҙаҡ числителдең модулен һәм знаменателде ҡушырға кәрәк: $5+2=7$ .

$-{\frac {15}{6}}$ кәсеренең бейеклеге $7$ .

Комментарий

Кәсерле һан (кәсер) термины ҡайһы берҙә рациональ һан терминына синоним булараҡ ҡулланыла, ә ҡайһы берҙә теләһә ниндәй бөтөн булмаған һандың синонимы. Һуңғы осраҡта кәсер һәм рациональ һандар төрлө әйберҙәр булалар, сөнки ул саҡта бөтөн булмаған рациональ һандар — кәсер һандарҙың бары айырым осрағы ғына.

Үҙсәнлектәре

Төп үҙсәнлектәре

Рациональ һандар күмәклеге ун алты төп үҙсәнлектәрҙе ҡәнәғәтләндерә, уларҙы бөтөн һандар үҙсәнлектәренән еңел сығарып була.^[1]

Тәртипкә килтерелгәнлек. Теләһә ниндәй $a$ $a$ һәм $b$ $b$ рациональ һандары өсөн, улар араһында өс бәйләнештең береһен һәм тик береһен генә бер мәғәнәле тура килтерергә мөмкинлек биргән ҡағиҙә бар: « $<$ $<$ », « $>$ $>$ » йәки « $=$ $=$ ». Был ҡағиҙә тәртипкә килтереү ҡағиҙәһе тип атала һәм түбәндәгесә әйтелә:
- ике $a={\frac {m_{a}}{n_{a}}}$ һәм $b={\frac {m_{b}}{n_{b}}}$ тиҫкәре булмаған һандар, ике бөтөн $m_{a}\cdot n_{b}$ һәм $m_{b}\cdot n_{a}$ һандары кеүек үк бәйләнеш менән бәйләнгәндәр;
- ике тиҫкәре $a$ һәм $b$ һандары, ике тиҫкәре булмаған $\left|b\right|$ һәм $\left|a\right|$ һандары кеүек үк бәйләнеш менән бәйләнгәндәр;
- әгәр $a$ тиҫкәре булмаһа, ә $b$ — тиҫкәре булһа, ул саҡта $a>b$ .
$\forall a,b\in \mathbb {Q} ~\left(a<b\lor a>b\lor a=b\right)$

Кәсерҙәрҙе ҡушыу
ҡушыу ғәмәле. Теләһә ниндәй $a$ һәм $b$ рациональ һандары өсөн ҡушыу бинар операцияһы бар, ул был һандарға ниндәйҙер $c$ рациональ һанын ярашлы ҡуя. Шуның менән бергә $c$ һаны үҙе $a$ һәм $b$ һандарының суммаһы тип атала һәм $\left(a+b\right)$ тип тамғалана, ә был һанды эҙләү процессы ҡушыутип атала. Ҡушыу ҡағиҙәһе түбәндәге күренештә: ${\frac {m_{a}}{n_{a}}}+{\frac {m_{b}}{n_{b}}}={\frac {m_{a}\cdot n_{b}+m_{b}\cdot n_{a}}{n_{a}\cdot n_{b}}}$ ; $\forall a,b\in \mathbb {Q} ~\exists !\left(a+b\right)\in \mathbb {Q} .$
ҡабатлау ғәмәле. Теләһә ниндәй $a$ һәм $b$ рациональ һандары өсөн ҡабатлау бинар операцияһы бар, ул был һандарға ниндәйҙер $c$ рациональ һанын ярашлы ҡуя. Шуның менән бергә $c$ һаны үҙе $a$ һәм $b$ һандарының ҡабатландығы тип атала һәм $\left(a\cdot b\right)$ тип тамғалана, ә был һанды эҙләү процессы ҡабатлау тип атала. Ҡабатлау ҡағиҙәһе түбәндәге күренештә: ${\frac {m_{a}}{n_{a}}}\cdot {\frac {m_{b}}{n_{b}}}={\frac {m_{a}\cdot m_{b}}{n_{a}\cdot n_{b}}}$ ; $\forall a,b\in \mathbb {Q} ~\exists \left(a\cdot b\right)\in \mathbb {Q}$ .
Тәртипкә килтереү бәйләнешенең транзитивлыҡ үҙсәнлеге. Теләһә ниндәй өс $a$ , $b$ һәм $c$ рациональ һаны өсөн әгәр $a$ бәләкәй $b$ һәм $b$ бәләкәй $c$ булһа, ул саҡта $a$ бәләкәй $c$ , ә әгәр $a$ тигеҙ $b$ һәм $b$ тигеҙ $c$ булһа, ул саҡта $a$ тигеҙ $c$ .
$\forall a,b,c\in \mathbb {Q} ~\left(a<b\land b<c\Rightarrow a<c\right)\land \left(a=b\land b=c\Rightarrow a=c\right)$ .
Ҡушыуҙың коммутативлығы Рациональ ҡушылыусыларҙың урынын алмаштырыуҙан сумма үҙгәрмәй.
$\forall a,b\in \mathbb {Q} ~~a+b=b+a$ .
Ҡушыуҙың ассоциативлығы Өс рациональ һанды ҡушыу тәртибе һөҙөмтәгә тәьҫир итмәй.
$\forall a,b,c\in \mathbb {Q} ~~\left(a+b\right)+c=a+\left(b+c\right)$ .
нулдең булыуы. Шундай 0 рациональ һаны бар, уны ҡушҡанда теләһә ниндәй башҡа рациональ һан үҙгәрмәй.
$\exists 0\in \mathbb {Q} ~\forall a\in \mathbb {Q} ~~a+0=a$ .
Ҡапма-ҡаршы һандарҙың булыуы Теләһә ниндәй рациональ һан өсөн ҡапма-ҡаршы рациональ һан бар. Ҡапма-ҡаршы һандарҙың суммаһы нулгә тигеҙ.
$\forall a\in \mathbb {Q} ~\exists \left(-a\right)\in \mathbb {Q} ~~a+\left(-a\right)=0$ .
Ҡабатлауҙың коммутативлығы. Рациональ ҡабатлашыусыларҙың урынын алмаштырыуҙан ҡабатландыҡ үҙгәрмәй.
$\forall a,b\in \mathbb {Q} ~~a\cdot b=b\cdot a$ .
Ҡабатлауҙың ассоциативлығы. Өс рациональ һанды ҡабатлау тәртибе һөҙөмтәгә тәьҫир итмәй.
$\forall a,b,c\in \mathbb {Q} ~~\left(a\cdot b\right)\cdot c=a\cdot \left(b\cdot c\right)$ .
берәмектең булыуы. Шундай 1 рациональ һаны бар, уға ҡабатлағанда теләһә ниндәй башҡа рациональ һан үҙгәрмәй.
$\exists 1\in \mathbb {Q} ~\forall a\in \mathbb {Q} ~~a\cdot 1=a$ .
Кире һандарҙың булыуы. Теләһә ниндәй нулдән айырмалы рациональ һан өсөн кире рациональ һан бар, үҙ-ара кире һандарҙың ҡабатландығы бергә тигеҙ.
$\forall a\in \mathbb {Q} ~\exists a^{-1}\in \mathbb {Q} ~~a\cdot a^{-1}=1$ .
Ҡабатлауҙың ҡушыуға ҡарата дистрибутивлығы. Ҡабатлау ғәмәле ҡушыу ғәмәле менән таратыу законы аша ярашлы:
$\forall a,b,c\in \mathbb {Q} ~~\left(a+b\right)\cdot c=a\cdot c+b\cdot c$ .
Тәртипкә килтереү бәйләнешенең ҡушыу ғәмәле менән бәйләнеше. Рациональ тигеҙһеҙлектең уң һәм һул яҡтарына бер үк рациональ һанды ҡушырға мөмкин.
$\forall a,b,c\in \mathbb {Q} ~~a<b\Rightarrow a+c<b+c$ .
Тәртипкә килтереү бәйләнешенең ҡабатлау ғәмәле менән бәйләнеше. Рациональ тигеҙһеҙлектең уң һәм һул яҡтарын бер үк ыңғай рациональ һанға ҡабатларға мөмкин.
$\forall a,b,c\in \mathbb {Q} ~~c>0\land a<b\Rightarrow a\cdot c<b\cdot c$ .
Архимед аксиомаһы. $a$ рациональ һаны ниндәй генә булмаһын, шунса берәмек алырға мөмкин, уларҙың суммаһы $a$ һанынан арта.
$\forall a\in \mathbb {Q} ~\exists n\in \mathbb {N} ~~\sum _{k=1}^{n}1>a$ .

Өҫтәлмә үҙсәнлектәре

Рациональ һандарға хас булған башҡа бөтә үҙсәнлектәрҙе төп үҙсәнлектәргә индермәйҙәр, сөнки улар туранан-тура бөтөн һандарҙың үҙсәнлектәренә таянмайҙар, ә килтерелгән төп үҙсәнлектәрҙән сығып йәки ниндәйҙер математик объекттың билдәләмәһе буйынса иҫбат ителергә мөмкиндәр. Ундай өҫтәлмә үҙсәнлектәр бик күп. Бында уларҙың тик бер нисәһен генә килтереү урынлы.

Тәртипкә килтереү бәйләнеше «>» (аргументтарҙың ҡапма-ҡаршы тәртибендә) шулай уҡ транзитивлы.
$\forall a,b,c\in \mathbb {Q} ~~a>b\land b>c\Rightarrow a>c$
Теләһә ниндәй рациональ һандың нулгә ҡабатландығы нулгә тигеҙ.
$\forall a\in \mathbb {Q} ~~a\cdot 0=0$
Бер тамғалы рациональ тигеҙһеҙлектәрҙе быуын быуынлап ҡушырға мөмкин.
$\forall a,b,c,d\in \mathbb {Q} ~~a>b\land c>d\Rightarrow a+c>b+d$
Рациональ һандар күмәклеге $\mathbb {Q}$ ялан була (теүәлерәк, бөтөн һандар $\mathbb {Z}$ ) ҡулсаһының кәсерҙәрҙе ҡушыу һәм ҡабатлау ғәмәлдәренә ҡарата бүлендектәр яланы.
$\left(\mathbb {Q} ,+,\cdot \right)$ — поле
Позицион иҫәпләү системаһында рациональ һан представляется периодик кәсер рәүешендә күрһәтелә. Улай ғына түгел, кәсерҙең периодик кәсер рәүешендә күрһәтелә алыуы ысын һандың рационаллеге критерийы булып тора.
Һәр рациональ һан алгебраик була.
$\mathbb {Q} \subset \mathbb {A}$
Теләһә ниндәй төрлө ике рациональ $a$ һәм $b$ һандары араһында бер генә булһа ла шундай $x$ рациональ һаны бар, $a<x$ һәм $x<b$ . (Бындай һанға миҫал рәүешендә $x=\textstyle {\frac {a+b}{2}}$ алырға мөмкин.) $a$ һәм $x$ , шулай уҡ $x$ һәм $b$ араһында шулай уҡ берәр генә булһа ла рациональ һан булыуы аңлашылып тора. Ошонан сығып, теләһә ниндәй төрлө ике рациональ $a$ һәм $b$ һандары араһында сикһеҙ күп рациональ һан бар. Икенсе төрлө әйткәндә, күрше торған ике рациональ һан юҡ. Айырып әйткәндә, иң бәләкәй ыңғай рациональ һан юҡ.
Иң ҙур һәм иң бәләкәй рациональ һан юҡ. Теләһә ниндәй рациональ $x$ һаны өсөн рациональ (һәм хатта бөтөн) $a$ һәм $b$ һандары бар, бында $a<x$ һәм $x<b$ .

Күмәклектең иҫәплелеге

Рациональ һандар һанын баһалау өсөн, рациональ һандар күмәклегенең ҡеүәтен табырға кәрәк. Рациональ һандар күмәклеге иҫәпле булыуы еңел иҫбатлана. Бының өсөн рациональ һандарҙы нумерлай торған алгоритм килтереү етә, йәғни рациональ һәм натураль һандар араһында биекция урынлаштыра. Шундай төҙөүгә миҫал булып ябай алгоритм хеҙмәт итә ала. Ябай кәсерҙәрҙең сикһеҙ таблицаһы төҙөлә, һәр $i$ -нсы юлдың һәр $j$ -сы бағанаһында ${\frac {i}{j}}$ кәсере урынлаша. Асыҡлыҡ өсөн был таблицаның юлдары һәм бағаналары берәмектән нумерланалар. Таблицаның күҙәүҙәре $\left(i,j\right)$ тип тамғалана, бында $i$ — таблицаның күҙәү урынлашҡан юлы номеры, ә $j$ — бағана номеры.

Килеп сыҡҡан таблица «бормалы-бормалы» түбәндәге формаль алгоритм буйынса урап сығыла.

Әгәр хәҙерге урыны $\left(i,j\right)$ шундай булһа, бында $i$ — таҡ, ә $j=1$ булһа, ул саҡта унан һуңғы урын итеп $\left(i+1,j\right)$ һайлана.
Әгәр хәҙерге урыны $\left(i,j\right)$ шундай булһа, бында $i=1$ , ә $j$ — йоп, ул саҡта унан һуңғы урын итеп $\left(i,j+1\right)$ һайлана.
Әгәр хәҙерге урын өсөн $\left(i,j\right)$ $\left(i+j\right)$ индекстар суммаһы таҡ булһа, ул саҡта унан һуңғы урын — $\left(i-1,j+1\right)$ .
Әгәр хәҙерге урын өсөн $\left(i,j\right)$ $\left(i+j\right)$ индекстар суммаһы йоп булһа, ул саҡта унан һуңғы урын — $\left(i+1,j-1\right)$ .

Был ҡағиҙәләр өҫтән аҫҡа ҡарап сығыла һәм артабанғы урын беренсе тура килеүсәнлек буйынса һайлап алына.

Ошондай урап сығыу процессында һәр яңы рациональ һанға сираттағы натураль һан ярашлы ҡуйыла. Йәғни $1/1$ кәсеренә 1 һаны ярашлы ҡуйыла, $2/1$ кәсеренә — 2 һаны, һ.б. Әйтергә кәрәк, тик ҡыҫҡармай торған кәсерҙәр генә нумерланалар. Ҡыҫҡармауҙың формаль билдәһе булып кәсерҙең числителе һәм знаменателенең иң ҙур уртаҡ бүлеүсеһе бергә тигеҙ булыуы тора.

Был алгоритмға эйәреп, бөтә ыңғай рациональ һандарҙы нумерлап сығып була. Был ыңғай рациональ һандар күмәклеге $\mathbb {Q} _{+}$ иҫәпле тигәнде аңлата. Ыңғай һәм тиҫкәре рациональ һандар күмәклектәре араһында еңел генә биекция урынлаштырып була, ябай ғына һәр рациональ һанға уға ҡапма-ҡаршы һанды ярашлы ҡуйып. Шулай итеп, тиҫкәре рациональ һандар күмәклеге лә $\mathbb {Q} _{-}$ иҫәпле. Уларҙың берекмәһе $\mathbb {Q} _{+}\cup \mathbb {Q} _{-}$ иҫәпле күмәклектәрҙең үҙсәнлеге буйынса шулай уҡ иҫәпле. Рациональ һандар күмәклеге иһә $\mathbb {Q} =\mathbb {Q} _{+}\cup \mathbb {Q} _{-}\cup \left\{0\right\}$ иҫәпле күмәклек менән сикле күмәклектең берекмәһе булараҡ шулай уҡ иҫәпле.

Әлбиттә, рациональ һандарҙы нумерлауҙың башҡа ысулдары ла бар. Мәҫәлән, бының өсөн Калкин — Уилф ағасы, Штерн — Броко ағасы йәки Фарей рәте кеүек структуралар менән файҙаланырға була.

Рациональ һандар күмәклегенең иҫәпле булыуы тураһында раҫлау ниндәйҙер аптырап ҡалыу тыуҙырырға мөмкин, сөнки тәү ҡарауға ул натураль һандар күмәклегенән күпкә киңерәк тигән тәьҫорат тыуа. Ысынында улай түгел һәм бөтә рациональ һандарҙы нумерлап сығыу өсөн натураль һандар етә.

Рациональ һандарҙың етерлек булмауы

Геометрияла Архимед аксиомаһының эҙемтәһе булып (юғарыла хәтергә алынғандан дөйөмөрәк аңлауҙа), $1/n$ күренешендәге рациональ һандар менән күрһәтелгән, теләгәнсә бәләкәй (йәғни, ҡыҫҡа) дәүмәлдәр төҙөү мөмкинлеге тора. Был факт рациональ һандар менән теләһә ниндәй геометрик алыҫлыҡтарҙы үлсәргә була тигән алдатҡыс тәьҫорат тыуҙыра. Бының дөрөҫ булмауын еңел күрһәтеп була.

Пифагор теоремаһынан билдәле булыуынса, тура мөйөшлө өсмөйөштөң гипотенузаһы уның катеттарының квадраттары суммаһынан квадрат тамыр итеп күрһәтелә. Шулай итеп берәмек катетлы тура мөйөшлө өсмөйөштөң гипотенуза оҙонлоғо ${\sqrt {2}}$ тигеҙ, йәғни квадраты 2-гә тигеҙ булған һанға.

Әгәр ${\sqrt {2}}$ һаны ниндәйҙер рациональ һан менән күрһәтелә тип уйлаһаҡ, шундай $m$ бөтөн һаны һәм шундай $n$ натураль һаны табып була, бында ${\sqrt {2}}={\frac {m}{n}}$ , шуның менән бергә ${\frac {m}{n}}$ кәсере ҡыҫҡармай торған, йәғни $m$ һәм $n$ һандары — үҙ-ара ябай.

Әгәр ${\sqrt {2}}={\frac {m}{n}}$ , ул саҡта $2={\sqrt {2}}\cdot {\sqrt {2}}={\frac {m}{n}}\cdot {\frac {m}{n}}={\frac {m^{2}}{n^{2}}}$ , йәғни $m^{2}=2n^{2}$ . Шулай итеп, $m^{2}$ һаны йоп, ләкин таҡ һандарҙың ҡабатландығы таҡ, был $m$ һаны үҙе лә йоп тигәнде аңлата. Тимәк шундай $k$ натураль һанын табып була, $m$ һанын $m=2k$ күренешендә күрһәтеп була. $m$ һанының квадраты $m^{2}=4k^{2}$ ,ләкин икенсе яҡтан $m^{2}=2n^{2}$ , тимәк $4k^{2}=2n^{2}$ , йәки $n^{2}=2k^{2}$ . Бынан алда $m$ һаны өсөн күрһәтелгәнсә, был $n$ һаны — $m$ кеүек үк йоп тигәнде аңлата. Ләкин ул саҡта был һандар үҙ-ара ябай була алмайҙар, сөнки икеһе лә 2-гә бүленә. Килеп сыҡҡан ҡапма-ҡаршылыҡ ${\sqrt {2}}$ һанының рациональ һан булмауын иҫбатлай.

Юғарыла әйтелгәндән сығып, яҫылыҡта, ә, тимәк һанлы күсәрҙә лә, шундай киҫектәр бар, улар рациональ һандар менән үлсәнә алмайҙар. Был рациональ һандар төшөнсәһен ысын һандарға тиклем киңәйтеү мөмкинлегенә килтерә.

Шулай уҡ ара ҡ

Иҫкәрмәләр

↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 30 — 31. — 672 с. — ISBN 5-482-00445-7.

Әҙәбиәт

И.Кушнир. Справочник по математике для школьников. — Киев: АСТАРТА, 1998. — 520 с.
П. С. Александров. Введение в теорию множеств и общую топологию. — М.: глав. ред. физ.-мат. лит. изд. «Наука», 1977
И. Л. Хмельницкий. Введение в теорию алгебраических систем

Ҡалып:Числа Ҡалып:Алгебраические числа

[ilyin-1] В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 30 — 31. — 672 с. — ISBN 5-482-00445-7.

[1]