Арифметика
Был мәҡәлә башҡорт Википедияһының һайланған мәҡәләләре исемлегенә керә. |

Ганс Себальд Бехам, XVI быуат
Арифме́тика (бор. грек. ἀριθμητική — ἀριθμός «һан» һүҙенән) — математиканың һандарҙы, улар араһындағы бәйләнеште һәм үҙсәнлектәрен өйрәнеүсе бүлеге. Арифметиканың өйрәнеү предметы булып һандар (натураль, бөтөн, рациональ, ысын, комплекслы һандар) һәм уларҙың үҙсәнлектәре тора. Арифметикала үлсәүҙәр, иҫәпләү ғәмәлдәре (ҡушыу, алыу, ҡабатлау, бүлеү) һәм иҫәпләү ысулдары ҡарала. Айырым бөтөн һандарҙың үҙсәнлектәрен өйрәнеү менән юғары арифметика, йәки һандар теорияһы шөғөлләнә. Теоретик арифметика һан төшөнсәһенә билдәләмә биреүгә һәм анализлауға иғтибар бүлә, ә формаль арифметика предикаттарҙың (логик хәбәр) һәм аксиомаларҙың логик төҙөлөштәренә таянып эш итә. Арифметика иң боронғо һәм иң мөһим математик фәндәрҙең береһе; ул алгебра, геометрия һәм һандар теорияһы менән тығыҙ бәйләнгән[1][2].
Арифметиканың барлыҡҡа килеүенең сәбәбе булып иҫәпләүҙәргә һәм ауыл хужалығын үҙәкләштергәндәге мәсьәләләр менән бәйле иҫәп-хисапҡа практик мохтажлыҡ тора. Фән хәл итеүҙе талап иткән мәсьәләләр менән бергә үҫешә. Арифметиканың үҫешенә грек математиктары ҙур өлөш индерә — атап әйткәндә, философтар-һандар ярҙамында донъяның бөтә законлыҡтарын аңларға һәм тасуирларға тырышыусы пифагорсылар. Урта быуаттарҙа арифметиканы, неоплатониктарға эйәреп, ете азат сәнғәт тип аталғандар иҫәбенә индергәндәр. Ул осорҙа арифметиканы төп практик ҡулланыу өлкәһе булып сауҙа, навигация, төҙөлөш тора. Ошоноң менән бәйле, тәү сиратта геометрик төҙөүҙәр өсөн кәрәк булған иррациональ һандарҙы яҡынса иҫәпләүҙәр ҙур әһәмиәткә эйә була. Арифметика бигерәк тә Һиндостанда һәм ислам илдәрендә йылдам үҫешә, уларҙан математик белемдең өр яңы ҡаҙаныштары Көнбайыш Европаға үтеп инә; Рәсәйҙә математик белем менән «гректарҙан да, һәм латиндарҙан да» танышалар.
Яңы осор тыуыу менән диңгеҙҙә йөҙөү астрономияһы, механикаһы, ҡатмарлашҡан коммерция иҫәпләүҙәре иҫәпләү техникаһына яңы талаптар ҡуя һәм арифметиканың артабанғы үҫешенә этәргес була. XVII быуат башында Непер логарифмдарҙы уйлап таба, ә аҙаҡ Ферма һандар теорияһын арифметиканың үҙ-аллы бүлеге итеп сығара. Быуат аҙағына иррациональ һан тураһында рациональ яҡынлауҙар эҙмә-эҙлелеге булараҡ төшөнсә формалаша, ә артабанғы йөҙ йыллыҡ дауамында Ламберттың, Эйлерҙың, Гаусстың хеҙмәттәре арҡаһында арифметика комплекслы дәүмәлдәр менән ғәмәлдәрҙе үҙ эсенә ала, һәм хәҙерге заман күренешен ала.
Арифметиканың артабанғы тарихы уның нигеҙҙәрен тәнҡит күҙлегенән ҡарау, уны дедуктив нигеҙләргә маташыу менән билдәле. Һан тураһында төшөнсәне теоретик нигеҙләүҙәр, беренсе сиратта, натураль һанға ҡәтғи билдәләмә биреү 1889 йылда әйтеп бирелгән Пеано аксиомалары менән бәйле. Арифметиканың формаль төҙөлөшөнөң ҡаршылыҡһыҙ булыуы Генцен тарафынан 1936 йылда күрһәтелә.
Дөйөм башланғыс белем биреүҙә арифметиканың нигеҙҙәренә элек-электән һәм өҙлөкһөҙ ҙур иғтибар бирелә.
Арифметика предметы
[үҙгәртергә | сығанаҡты үҙгәртеү]
Арифметиканың предметы булып һанлы күмәклектәр, һандарҙың үҙсәнлектәре һәм һандар өҫтөндә ғәмәлдәр тора[3]. Уға шулай уҡ иҫәпләү техникаһы, үлсәүҙәр[4], һан төшөнсәһенең барлыҡҡа килеүе һәм үҫеше менән бәйле мәсьәләләрҙе лә индерәләр[1]. Арифметика, тәү сиратта, натураль һандарҙы һәм кәсерҙәрҙе өйрәнә[5]. Натураль һандар күмәклегенең аксиоматик структураһы нигеҙендә, бөтөн, ысын һәм комплекслы һандарҙы ла индереп, башҡа һандар күмәклеген төҙөү тормошҡа ашырыла, уларҙы анализлау яһала[1]. Ҡайһы берҙә арифметика сиктәрендә шулай уҡ кватерниондар һәм башҡа гиперкомплекслы һандар ҡарала. Шуның менән бергә, Фробениус теоремаһынан, һан төшөнсәһен уның ниндәй ҙә булһа арифметик үҙсәнлеген юғалтмайынса комплекслы яҫылыҡтан ситкә киҫәйтеү мөмкин түгел икәне килеп сыға[6][7].
Һандар өҫтөндә төп ғәмәлдәргә ҡушыу, алыу, ҡабатлау һәм бүлеүҙе[3], һирәгерәк — дәрәжәгә күтәреүҙе, тамыр алыуҙы[4] һәм һанлы тигеҙләмәләрҙе сығарыуҙы индерәләр[3]. Арифметик ғәмәлдәрҙең тарихи исемлеге шулай уҡ иҫәпләүҙе, икеләтеүҙе (ҡабатлауҙан башҡа), икегә бүлеүҙе һәм ҡалдыҡлы бүлеүҙе (бүлеүҙән башҡа), арифметик һәм геометрик прогрессияларҙың суммаларын табыуҙы индерә[8]. Джон Непер үҙенең «Логистическое искусство» китабында арифметик ғәмәлдәрҙе баҫҡыстарға бүлә: түбәнге баҫҡыста ҡушыу һәм алыу тора, артабанғыһында — ҡабатлау һәм бүлеү, артабан — дәрәжәгә күтәреү һәм тамыр алыу[9]. Билдәле методист И. В. Арнольд өсөнсө баҫҡыс ғәмәлдәргә шулай уҡ логарифмлауҙы ла индерә[10]. Ғәҙәттә арифметика тип, «квадратик формалар арифметикаһы», «матрицалар арифметикаһы» кеүек, төрлө объекттар өҫтөндә ғәмәлдәр башҡарыуҙы атайҙар[1].
Асылда, практик ихтыяж өсөн кәрәк булған математик иҫәпләүҙәрҙе һәм үлсәүҙәрҙе (пропорциялар, проценттар, өсләтә ҡағиҙә), түбәнге, йәки практик арифметикаға индерәләр[3], шул уҡ ваҡытта логик анализ кеүек һан төшөнсәләрен теоретик арифметикаға индерәләр[1]. Бөтөн һандарҙың үҙсәнлектәре, уларҙы өлөштөргә бүлеү, өҙлөкһөҙ кәсерҙәрҙе төҙөү һандар теорияһының состав өлөшө булып тора[1], уны оҙаҡ ваҡыт юғары арифметика тип иҫәпләйҙәр[3]. Арифметика шулай уҡ алгебра менән тығыҙ бәйләнгән, ул ғәмәлдә операцияларҙы һандарҙың үҙенсәлектәрен һәм үҙсәнлектәрен иҫәпкә алмайынса өйрәнә[1][11]. Дәрәжәгә күтәреү һәм тамыр алыу кеүек арифметик ғәмәлдәр алгебраның техник өлөшө булып тора. Ошоноң менән бәйле, Ньютон һәм Гаусс артынса, алгебраны арифметиканы дөйөмләштереү тип иҫәпләү ҡабул ителгән[3][4]. Дөрөҫөн әйткәндә, арифметика, элементар алгебра һәм һандар теорияһы араһында аныҡ ҡына сик юҡ. БСЭ-ла әйтелә: «Алгебра хәреф тамғалауҙарын ҡулланып, һандар системаларының дөйөм үҙсәнлектәрен һәм мәсьәләләрҙе тигеҙләмәләр ярҙамында сисеүҙең дөйөм ысулдарын өйрәнә; арифметика конкрет бирелгән һандар менән иҫәпләү алымдары, ә үҙенең юғарыраҡ өлкәләрендә (ҡарағыҙ. Һандар теорияһы) — һандарҙың нескәрәк индивидуаль үҙсәнлектәре менән шөғөлләнә»[12].
Башҡа академик фәндәр кеүек үк, арифметика ла принципиаль методологик проблемаларға юлыға; уның өсөн аксиомаларҙың ҡаршылыҡһыҙ һәм тулы булыу мәсьәләләрен тикшерергә кәрәк[3]. Арифметиканың предикаттар һәм аксиомаларының формаль системаһын логик төҙөү менән формаль арифметика шөғөлләнә[2].
Иң ябай төшөнсәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]Рәт һандары, натураль һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]
Иң ябай арифметик төшөнсә булып рәт һандары тора. Иҫәпләү объекты булып төрлө элементтар йәки уларҙың күмәклектәре тора, мәҫәлән, алмалар һәм алмалар кәрзине. Рәт һаны ярҙамында элементтарҙы нумерларға һәм уларҙың дөйөм иҫәбен тамғаларға мөмкин.
Рәт һаны билдәле бер тигеҙ һандағы элементтары булған төркөмдәр менән иҫәпләүгә бәйле — мәҫәлән, алманы тиҫтәләп иҫәпләү. Ғәҙәттә был ике ҡулдағы бармаҡтар (нигеҙе -ға тигеҙ), ләкин тарихи сығанаҡтарҙа -ешәрләп төркөмләүҙәр бар. Төркөмдәге элементтар һаны иҫәпләү системаһы өсөн нигеҙ булып тора[11].
Иҫәпләүҙә килеп сыҡҡан һанлы рәтте натураль тип, ә уның элементтарын — натураль һандар тип атайҙар. Натураль рәт төшөнсәһе тәү башлап грек математигы Никомахтың хеҙмәттәрендә б. э. I быуатында, ә натураль һан төшөнсәһе — рим авторы Боэций хеҙмәттәрендә V быуат аҙағы — VI быуат башында осрай. Терминды дөйөм ҡулланыу XVIII быуатта Д’Аламбер хеҙмәттәренән башлана. Архимед үҙенең «Псаммит» исемле хеҙмәтендә, һандар рәтен сикһеҙ дауам итергә мөмкин тип әйтә, ләкин шуның менән бергә, реаль мәсьәләләр өсөн ҙур булмаған киҫеге лә етә тип әйтеп ҡуя[13]. Натураль һандарҙы пифагорсылар йоп һәм таҡ һандарға бүлгән тип иҫәпләйҙәр, ул шулай уҡ мысырлы Ринд папирусында ла бар. Пифагорсылар шулай уҡ ябай һәм ҡушма һандарҙы ла билдәләгәндәр[14].
Ҡушыу, ҡабатлау, дәрәжәгә күтәреү
[үҙгәртергә | сығанаҡты үҙгәртеү]
Натураль һандар өсөн ҡушыу һәм ҡабатлау ғәмәлдәре тәбиғи рәүештә билдәләнгәндәр. Күпмелер һанда предметтары булған ике йыйылманы берләштергәндә, яңы йыйылмала тәүге ике йыйылмала бергә булған тиклем предмет була. Әгәр беренсе йыйылмала предмет, ә икенсеһендә — предмет булһа, уларҙың суммаһында предмет була. Күрһәтелгән ғәмәл ҡушыу тип атала һәм иң ябай бинар операция булып тора[4]. Сумманың дөрөҫлөгөн тикшереү өсөн ҡушыу таблицаһын белеү мотлаҡ түгел, предметтарҙы һанап сығыу етә[15].
Бер нисә бер төрлө күмәклектәрҙең элементтарын күп тапҡыр ҡушыу был күмәклектәрҙең тәртибенә бәйле түгел, был икенсе бинар операцияны — ҡабатлауҙы билдәләргә мөмкинлек бирә[4]. Ҡабатлауҙан башҡа, борон айырым арифметик ғәмәл — икеләтеү, йәки икегә ҡабатлау булған[16].
Ҡабатлауға ҡушыу аша билдәләмә биреүгә оҡшаш рәүештә, күп тапҡыр ҡабатлау дәрәжәгә күтәреү ғәмәлен билдәләргә мөмкинлек бирә.
Арифметиканың төп закондары
[үҙгәртергә | сығанаҡты үҙгәртеү]
Был ғәмәлдәрҙең үҙсәнлектәре тураһында биш закон әйтеп бирелгән, улар арифметиканың төп закондары тип иҫәпләнәләр[17]:
- Ҡушыуҙың Коммутативлыҡ: урын алмаштырыу законы ҡушылыусыларҙың урынын алмаштырыуҙан сумма үҙгәрмәй ти. Шундай уҡ закон ҡабатлау өсөн дә билдәле, ләкин унда, әлбиттә, ҡабатлашыусылар һәм ҡабатландыҡ тураһында әйтелә. Был закондарҙы алгебраик формала хәрефтәр менән тамғалап әйтеп бирергә мөмкин:
- Ҡушыуҙың Ассоциативлыҡ: төркөмләү законы бер нисә ҡушылыусыны ҡушҡанда, уларҙы теләһә ниндәй тәртиптә төркөмләргә мөмкин тип әйтә. Ҡабатлау өсөн шуға оҡшаш законда ҡабатлашысыларҙы ҡабатлау тураһында әйтелә. Был закондарҙы шулай уҡ алгебраик формала күрһәтергә мөмкин:
- Дистрибутилыҡ: таратыу законы әйтә: сумманы һанға ҡабатлау өсөн, һәр ҡушылыусыны был һанға ҡабатларға һәм килеп сыҡҡан ҡабатландыҡтарҙы ҡушырға мөмкин. Алгебраик формала:
Арифметиканың төп закондарынан тыш, натураль һандар өсөн шулай уҡ ҡушыуҙың һәм ҡабатлауҙың монотонлыҡ законы үтәлә[18][19], алгебраик формала ошолай яҙыла:
- булғанда ;
- һәм булғанда .
Урын алмаштырыу законы өсөн «коммутатив» терминын 1814 йылда француз математигы Сервуа индерә. Төркөмләү законы өсөн «ассоциатив» терминын 1853 йылда Гамильтон индерә[17].
Пуанкаре бөтә арифметик ғәмәлдәрҙе һәм закондарҙы интуиция күҙлегенән сығып ҡарай. Закондар бәләкәй һандар өсөн һис шикһеҙ үтәләләр, һәм индукция ҡағиҙәһен ҡулланып, улар бөтә һандар өсөн дә үтәләләр тип һығымта яһарға мөмкин тип раҫлай. Икенсе ҡараш буйынса, артабанғы иҫбатлауҙар логик төҙөлөш менән бәйле булған ваҡытта, бөтә закондар ҙа түгел, ә иң ябай закондар ғына интуитив үтәлмәле булып һаналалар[20]. Урын алмаштырыу һәм төркөмләү закондары һис шикһеҙ үтәлә тип иҫәпләнә[17]. Таратыу, йәки дистрибутив законды Евклид үҙенең «Башланғыстарында» геометрик ысул ҡулланып иҫбатлаған[21].
Дәрәжәгә күтәреү операцияһы коммутатив та, ассоциатив та түгел, уның үҙенең ҡағиҙәләре. Был операцияны башҡарыуҙың төп ҡағиҙәләре ыңғай дәрәжәләр өсөн уның билдәләмәһенән асыҡ күренеп торалар[4]. Алгебраик формала улар ошолай яҙылалар:
- Дистрибутивлыҡ — дәрәжәгә күтәреү операцияһы өсөн таратыу законы:
-
- шул уҡ, алыу осрағында, кәсер күренешен ала:
- Ҡабаттан дәрәжәгә күтәреү дәрәжә күрһәткестәрен ҡабатлау була:
- .
Кире операциялар
[үҙгәртергә | сығанаҡты үҙгәртеү]Арифметиканың бөтә операцияларының да киреһе бар: ҡушыуҙың — алыу, ҡабатлауҙың — бүлеү, дәрәжәгә күтәреүҙең — арифметик тамыр алыу һәм логарифм. Ҡушыу һәм ҡабатлауҙың, уларҙың бинар операция булыуына ҡарамаҫтан берәр генә кире операциялары булыуы, уларҙың коммутативлығы менән аңлатыла.
Алыу: тиҫкәре һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]
Алыу — ул ҡушыуға кире ғәмәл: ике һәм һандарының айырмаһы тигеҙләмәһенән була [4]. Алыу операцияһы «−» тамғаһы менән яҙыла һәм күренешендә яҙыла. Операцияны башҡарыу өсөн ике ысул ҡулланалар: кәмеүсенән кәметеүсенең берәмектәрен һанап алыу йәки кәметеүсегә ҡушҡанда кәмеүсене биргән һанды һайлап алыу[16].
Әгәр алыу операцияһын, ҡушыу операцияһы сиктәрендә сумма һәм ҡушылыусы була алған һандарға ғына түгел. ә бөтә натураль һандар парына ҡулланһаң, натураль рәттән ситкә сығырға юл ҡуя, йәғни ике натураль һандың айырмаһы мотлаҡ натураль һан түгел — алыу һөҙөмтәһендә нуль йәки тиҫкәре һан килеп сығырға мөмкин. Тиҫкәре һандарҙы предметтар һаны итеп ҡарап булмай инде, һанлы күсәрҙә улар нулдән һулдараҡ урынлашҡандар. Натураль һандарға тиҫкәре һандарҙы һәм нулде өҫтәгәндән килеп сыҡҡан һандар күмәклеге бөтөн һандар күмәклеге тип атала. Нуль һәм натураль һандар күмәклеге тиҫкәре булмаған бөтөн һандар күмәклеге тип атала[4]. Ҡабатлағанда, һандарҙың ҡабатландығы ыңғай йәки тиҫкәре буламы икәнен асыҡлау өсөн, «тамғалар ҡағиҙәһен» ҡулланалар[22].
Тиҫкәре һандарҙы XIX быуатҡа тиклем бик күп математиктар ысын түгел һәм мәғәнәһеҙ тип иҫәпләгәндәр, әммә был уларҙы бөтә ерҙә формаль ҡулланыуға ҡамасауламай. Тәү башлап тиҫкәре һан төшөнсәһе Һиндостанда барлыҡҡа килә, унда тиҫкәре һандарға «бурыс» мәғәнәһе биргәндәр (ыңғай һандар — «байлыҡ»). Тиҫкәре һандар тик XVII быуатта ғына таралыу алғандар[23]. «Алыу» термины Боэцийҙа уҡ күренә, «кәмеүсе» һәм «кәметеүсе» терминдарын Вольф 1716 йылда, «айырма» терминын — Видман 1489 йылда ҡулланыуға индерә[16]. Хәҙерге «+» һәм «−» билдәләре менән тамғалауҙы шулай уҡ Видман XV быуат аҙағында индерә.
Бүлеү: рациональ һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]
Бүлеү ҡабатлауға кире ғәмәл булып тора. Бүлеүҙең беренсе билдәләмәһе — бүленеүселә бүлеүсенең берәмектәре тапҡыр булған һанды табыу ул. Ошондай билдәләмә XIV быуат арифметика дәреслектәрендә бирелгән — мәҫәлән, . Бүлеү бик ҡатмарлы һәм ауыр операция һаналған. Бүлеүсенең бүлендектең айырым разрядтарына өлөшләтә ҡабатландығын ҡулланған хәҙерге бүлеү ысулы (бағаналап бүлеү), 1460 йылғы итальян манускриптында килтерелгән[16].
Ҡабатлашыусы һәм ҡабатландыҡ булмаған натураль һандар өсөн ҡалдыҡлы бүлеү операцияһы билдәле (ғәмәлдә бүлеүҙән ҡалдыҡтың билдәләмәһе шулай уҡ модуле буйынса бүлеү тип атала). Шулай уҡ төрлө айырым осраҡтарҙа бүлеүҙе ябайлаштырыусы йәки теге йәки был һанға бүленеүсәнлеген тикшерергә мөмкинлек биргән күп ысулдар бар. Мәҫәлән:
- әгәр һандың унарлы яҙыуында һуңғы цифры икегә бүленһә, һан икегә ҡалдыҡһыҙ бүленә;
- әгәр һандың унарлы яҙыуында цифрҙары суммаһы өскә бүленһә, был һан өскә ҡалдыҡһыҙ бүленә;
- әгәр һандың унарлы яҙыуында һуңғы цифры ноль булһа, һан унға ҡалдыҡһыҙ бүленә.
Әгәр натураль һандарҙы ҡабатлап табып булған һандарҙы ғына бүлмәһәң, шул уҡ ваҡытта ҡалдыҡты айырып алмаһаң, бүлеү операцияһы, алыу кеүек үк, натураль һандар күмәклегенән ситкә сығырға юл ҡуя. Бүлгәндә ҡалдыҡһыҙ бөтөнгә тиклем ҡыҫҡартырға мөмкин булмаған кәсерҙәр килеп сығырға мөмкин. Шундай кәсерҙәргә ярашлы һандар рациональ һандар тип аталалар. Рациональ һандарҙы бүлеүгә нигеҙләнгән тағы ла билдәле һандар төрөн киңәйтеү килеп сыға. Тарихи тәүҙә кәсер төшөнсәһе барлыҡҡа килә, ә аҙаҡ тиҫкәре һан төшөнсәһе[24]. Мәктәп курсында ла шундай уҡ тәртип ҡабул ителгән[25].
Кәсерҙәрҙе яҙыуҙың ике формаһы ҡулланыла — горизонталь йәки ҡыя һыҙыҡ менән бүленгән һәм йыш ҡына минималь һандарға тиклем ҡыҫҡартылған числитель һәм знаменатель, һәм һандың позицион яҙылышында бөтөн һәм кәсер өлөшөн айырыусы тамғанан һуң урынлашыусы кәсер өлөшөнөң цифрҙары рәүешендә. Мәҫәлән, 10-ды 20-гә бүлеү һөҙөмтәһе күренешендә яҙыл.
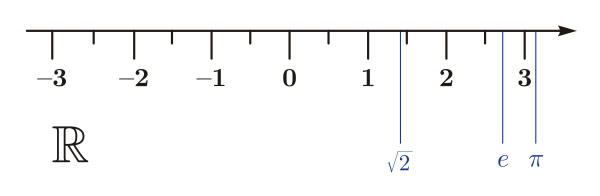
Тамыр алыу: иррациональ һәм комплекслы һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]Дәрәжәгә күтәреү өсөн ике кире операцияның берәүһе — тамыр алыу, йәки ярашлы дәрәжәгә күтәргәндә билдәле һөҙөмтәне биргән һанды табыу. Йәғни, алгебра теле менән әйткәндә, күренешендәге тигеҙләмәнең тамырын табыу. Икенсе кире операция — логарифмды эҙләү ( күренешендәге тигеҙләмәнең тамырын табыу). Арифметикаға, ҡағиҙә булараҡ, тик икенсе дәрәжә тамырҙы — квадрат тамырҙы иҫәпләүҙе генә индерәләр.
Тамырҙы иҫәпләү операцияһы, әгәр уны натураль һандарҙы дәрәжәгә күтәреп табып булған һандар өсөн генә ҡулланмаһаң, ҡалған кире операциялар кеүек үк, натураль һандар күмәклегенән ситкә сығырға мәжбүр итә. Был осраҡта килеп сыҡҡан һандар, йыш ҡына, сикле рациональ кәсерҙәр рәүешендә күрһәтелә алмайҙар, һәм шуға күрә иррациональ һандар тип аталалар. Рациональ һандарға иррациональ һандарҙы өҫтәүҙән килеп сыҡҡан һандар күмәклеген, әйберләтә йәки ысын һандар тип атайҙар.
Боронғо Грецияла уҡ үлсәүҙәш булмаған киҫектәр булыуы билдәле булған, кәм тигәндә, яғы бер берәмек итеп алынған квадраттың яғы һәм диагонале миҫалында, һәм улар өсөн теүәл һан ҡиммәте табырға маташҡандар, был Евклидтың «Башланғыстарында» сағылыш таба. Ысын һандар тик XVII—XVIII быуаттарҙа ғына тикшеренеү объекты булалар. XIX быуаттың икенсе яртыһында Дедекинд, Кантор һәм Вейерштрасс үҙҙәренең ысын һанды билдәләүҙең конструктив ысулдарын әйтеп бирәләр[26].
Тамыр алыу операцияһы өсөн ошондай ҡағиҙә билдәле[4]:
- .
Һандар күмәклеген артабан киңәйтеү тиҫкәре һандан квадрат тамыр алыу мөмкин булмауы менән бәйле. Ошондай проблемаға борон квадрат тигеҙләмәләрҙе сығарғанда юлыҡҡандар, һәм ундай тигеҙләмәләрҙе сисеүе мөмкин булмаған тигеҙләмәләр тип иҫәпләгәндәр. XVI быуаттың беренсе яртыһында бындай тигеҙләмәләрҙең сығарылышын тиҫкәре һандарҙан тамыр аша күрһәтә башлағандар һәм ундай тамырҙарҙы «уйланма», «мөмкин булмаған», «уйҙағы» һәм башҡа төрлө атай башлағандар[27]
Практик арифметика
[үҙгәртергә | сығанаҡты үҙгәртеү]Арифметиканың практик яғы теүәл арифметик ғәмәлдәрҙе башҡарыу ысулдарын, схемаларын һәм алгоритмдарын, шулай уҡ яҡынса иҫәпләүҙең төрлө алымдарын, шул иҫәптән ҡайһы бер үлсәүҙәрҙә теүәл ҡиммәтте табыу мөмкин булмағанлыҡтан барлыҡҡа килгән һәм уның тәртибен, йәғни тәүге мәғәнәле цифрҙарын асыҡларға ярҙам итеүсе иҫәпләү машиналарын һәм башҡа яйланмаларҙы үҙ эсенә ала[28].
- Иң ябай иҫәпләү ҡорамалдары
Теүәл ысулдар
[үҙгәртергә | сығанаҡты үҙгәртеү]XV быуаттан башлап күп урынлы һандар өҫтөндә арифметик операцияларҙы башҡарыу өсөн төрлө алгоритмдар тәҡдим ителә, улар аралаш иҫәпләүҙәрҙе яҙыу характеры менән айырылалар[1]. Арифметик алгоритмдар, теләһә ниндәй ыңғай ысын һан берҙән бер ысул менән
- күренешендә күрһәтелә алған, ғәмәлдәге позицион иҫәпләү системаһында төҙөлгәндәр, бында — һанының яҙылышында сираттағы цифр, — иҫәпләү системаһының нигеҙе, — һанының бөтөн өлөшөнөң разрядтары һаны .
Һандар өҫтөндә бөтә ғәмәлдәр унға тиклем ҡушыу һәм ҡабатлау таблицаларын һәм төп арифметик закондарҙы ҡулланалар. Иллюстрация сифатында билдәле фәнде популярлаштырыусы Клейн ошондай миҫал килтерә:
бында таратыу һәм төркөмләү закондары ҡулланыла[29].
Тиҙ һәм теүәл иҫәпләүгә булған ихтыяж иң ябай иҫәпләү яйланмалары төҙөүгә килтерә: абак, суаньпаня, юпана йәки счёт. Артабанғы аҙым булып Отред тарафынан 1622 йылда логарифмик линейка төҙөү тора, ул ҡабатлау һәм бүлеү ғәмәлдәрен башҡарырға мөмкинлек бирә[30].
Компьютер арифметикаһы
[үҙгәртергә | сығанаҡты үҙгәртеү]
Кнут арифметик ғәмәлдәрҙе «компьютерҙар өлөшө» тип һанай[31]. Дүрт арифметик ғәмәлде механикалаштырырға мөмкинлек биргән беренсе иҫәпләү машиналарының конструкцияһы XVII быуатта төҙөлә. Үҙе атағанса Шиккардтың «арифметик машинаһы» 1623 йылда төҙөлә. Ҡушыу һәм алыу операциялары цилиндрҙарҙы өйрөлтөү ярҙамында башҡарыла, шулай уҡ ҡабатлау һәм бүлеү өсөн дә махсус цилиндрҙар булған. Бынан тыш, машина тиҫтәләрҙе күсерә алған. Паскалдың машинаһы уның тарафынан 1642 йылда атаһына финанс иҫәп-хисабын башҡарыуҙа ярҙам итеү өсөн эшләнә. Уның эшләү принцибы Шиккард машинаһыныҡы кеүек үк була. Машинаның төп өлөшөн тиҫтәләрҙе күсереү механизмы тәшкил итә. Шуның менән бергә, бындай машиналарҙы һөнәрселек хеҙмәте менән эшләү файҙаһыҙ булып ҡала[32]. Арифмометрҙы камиллаштырырға маташыуҙар бөтә XVIII быуат дауамында бара, ләкин тик XIX быуатта арифмометрҙарҙы ҡулланыу киң таралыу ала[33].
XX быуатта арифмометрҙарға алмашҡа электрон иҫәпләү машиналары килә. Уларҙың нигеҙендә арифметик ғәмәлдәрҙе башҡарыу өсөн иң әҙ һанда элементар операциялар ҡулланған алгоритмдар ята[1]. Компьютер арифметикаһы күсеп йөрөүсе өтөрлө һандар, кәсерҙәр һәм бик ҙур һандар өҫтөндә операциялар башҡарыу алгоритмдарын үҙ эсенә ала[31].
Үлсәү
[үҙгәртергә | сығанаҡты үҙгәртеү]Иҫәпләргә кәрәк булған предметтарҙан тыш үлсәргә мөмкин булған предметтар бар — беренсе сиратта был оҙонлоҡ һәм масса[34].
Иҫәпләгәндәге кеүек, кешенең беренсе оҙонлоҡ үлсәме булып ҡулының бармаҡтары тора. Унан һуң алыҫлыҡты аҙымдарҙа, икеләтә аҙым менән, милдәрҙә (мең икеләтә аҙым), стадийҙарҙа (боронғо грек оҙонлоҡ берәмеге, яҡынса 150—190 метрға тигеҙ) үлсәй башлағандар. Бынан тыш, оҙонлоҡто үлсәү өсөн терһәк, ус аяһы, сажиндар, дюймдарҙы ҡуллана башлағандар. Төрлө төбәктәрҙә үҙҙәренең үлсәү системаһы булған, улар бик һирәк унға бүленгән[35]. Үлсәү берәмектәренең күп төрлөлөгө, айырым алғанда, кәсер ҡулланмаҫҡа мөмкинлек бирә[36][37]. Сауҙа арифметикаһы унарлы булмаған иҫәпләү системаһында дәүмәлдәр (аҡса берәмектәре, оҙонлоҡ һәм ауырлыҡ берәмектәре) менән эш итә белеүҙе үҙ эсенә ала[38].
XVIII быуат аҙағында француз революцион хөкүмәте тарафынан ваҡытлыса, ә аҙаҡ архив (1799 йылдың 10 декабрендәге закон) метр нигеҙендә үлсәүҙәрҙең метр системаһы ҡабул ителә (Франция уға тулыһынса 1840 йылдың 1 ғинуарынан күсә). Метр менән бер рәттән килограмм билдәләнә. Метр системаһының нигеҙендә унарлы система ята. Тап ошо хәл уға бөтә донъяға тиерлек таралырға мөмкинлек бирә лә инде (Бөйөк Британия һәм АҠШ-ты иҫәпкә алмағанда). Парижда урынлашҡан Халыҡ-ара үлсәмдәр һәм ауырлыҡтар бюроһының махсус ҡарары буйынса, 1888 йылда платина һәм иридийҙың иретмәһенән халыҡ-ара метр һәм халыҡ-ара килограмм — үлсәм һәм ауырлыҡ эталоны әҙерләнә. Ваҡыт һәм мөйөш үлсәмдәренән тыш, бөтә ҡалған үлсәү берәмектәре шулай уҡ унарлы иҫәпләү системаһы менән бәйле[39].
Яҡынса ысулдар
[үҙгәртергә | сығанаҡты үҙгәртеү]Яҡынса иҫәпләүҙәр тарихи рәүештә берәмек квадраттың диагоналенең оҙонлоғон иҫәпләгәндә барлыҡҡа килә, ләкин унарлы системаға күскәндә һәм иррациональ һандар һәм сикһеҙ периодлы кәсерҙәр менән күрһәтелгән һандар урынына сикле унарлы кәсерҙәрҙе ҡулланғанда киң таралыу алалар[40].
Баһалаусы иҫәпләүҙәр өсөн, беренсе сиратта, монотонлыҡ закондарын ҡулланалар. Мәҫәлән, ҡабатландығының тәртибен асыҡлау өсөн, түбәндәге баһалау менән файҙаланырға мөмкин: [29].
Һандар теорияһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Һандар теорияһы, йәки юғары арифметика, — бөтөн һандар тураһындағы фән, ул һандарҙың бүленеүсәнлеге менән бәйле арифметик мәсьәләләрҙән килеп сыҡҡан[41]. Элементар һандар теорияһы, ғәҙәттә уйланма һандарҙы ҡулланмайынса, элементар ысулдар менән хәл ителгән мәсьәләләр менән эш итә. Уларға бүленеүсәнлек теорияһын, сағыштырыуҙар теорияһын, аныҡ булмаған тигеҙләмәләрҙе, ҡушылыусыларға тарҡатыуҙы, рациональ һандар менән яҡынлашыуҙарҙы, сынйырлы кәсерҙәрҙе индәрәләр[42]. Арифметиканың төп теоремаһы — һанды ябай ҡабатлашыусыларға берҙән-бер ысул менән тарҡатыу тураһында — шулай уҡ һандарҙың элементар теорияһының өлөшө булып тора[43].
Бөтөн һандарҙың, ябай һандар, ҡушма һандар, квадрат, камил һандар кеүек айырым аҫкластары, боронғо мысырлылар тарафынан уҡ айырылған булған. Улар пифагор өсәүен, иң ҙур уртаҡ бүлеүсене табыу өсөн формула сығарғандар, ябай һандарҙың сикһеҙ икәнен күрһәткәндәр. Диофант ябай һандар менән бәйле мәсьәләләрҙе системалаштырған. Диофанттың эшен XVII быуатта Ферма һәм XVIII быуатта Эйлер дауам итәләр. Ферма бөтөн һандарҙа тигеҙләмәләр сығарыу менән шөғөлләнгән һәм иҫбатламайынса бәләкәй һәм Ферманың бөйөк теоремаһын әйтеп биргән. Эйлер, Ферманың тикшеренеүҙәрен дауам итеп, Ферманың бәләкәй теоремаһын һәм Ферманың бөйөк теоремаһының айырым осрағын иҫбат итә. Ул беренсе булып һандар теорияһы мәсьәләләрен сығарыу өсөн математик анализды ҡуллана һәм аналитик һандар теорияһын барлыҡҡа килтерә. Эйлер яһаусы функцияларҙы билдәләй, улар нигеҙендә әйләнмәле ысул һәм тригонометрик суммалар ысулы төҙөлә[41].
Хәҙерге ваҡытта, элементар һәм аналитик һандар теорияһынан тыш, аддитив, алгебраик, ихтималлыҡ, метрик кеүек һандар теориялары бүлектәре бар[41].
Теоретик арифметика
[үҙгәртергә | сығанаҡты үҙгәртеү]Хәҙерге заман математикаһында теорияны төҙөү төп үҙсәнлектәрен, йәки аксиомаларын һайлауҙан ғибәрәт, уларҙан дөйөм ҡабул ителгән логика ярҙамында теорияның бөтә ҡағиҙәләрен, йәки теоремаларын сығарыу талап ителә[44]. Арифметиканы теоретик төҙөү алгебраик төшөнсәләр менән эш итә. Арифметиканың төп билдәләмәләрен айырып алыу ҡатмарлылығы уның башланғыс ҡағиҙәләренең ябайлығы менән бәйле. Пеано, һүҙҙәрҙе ҡулланғанда ялған ассоциатив рәттән һаҡланып, иҫбатлауҙарҙы, уҙе алдан ҡабул иткән ҡағиҙәләргә генә таянып, тик символдар телендә башҡара. Кантор һәм Дедекинд һандарҙы күмәклектәр һәм улар өҫтөндә абстракт бәйләнештәр менән бәйләйҙәр[20]. Күмәклектәр теорияһы арифметик ғәмәлдәрҙе, бер элемент башҡа ике элемент аша билдәләнгән, өс элемент араһында айырым бәйләнештәр, йәки алгебраик операциялар итеп ҡарай[45]. Күмәклектәр теорияһы тураһында һөйләгәндә Клейн, бындай ҡарашта теорияның үҫеше «ситләштерелгән һәм аңлайышһыҙ» булып китә тип әйтә[20].
Натураль һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]1810 йылда чех математигы Больцано натураль һандар өсөн ҡушыу ғәмәленә билдәләмә бирә. Уға бәйһеҙ рәүештә немец математиктары Грассман 1861 йылда һәм Ганкель 1869 йылда оҡшаш билдәләмә бирәләр[46]. «Элементар математика энциклопедияһы» натураль һандарҙы ҡушыуға ошондай билдәләмә тәҡдим итә[47]:
|
Билдәләмә. Натураль һандарҙы ҡушыу тип, һәр һәм натураль һандар парына түбәндәге үҙсәнлектәргә эйә булған бер һәм бары бер генә натураль һанын ярашлы ҡуйған ярашлыҡ атала:
|
Натураль һандарҙы ҡушыу һәр ваҡыт үтәлеүсән һәм бер мәғәнәле[47].
Ҡабатлауға, ҡушыу кеүек үк, бер береһенә бәйһеҙ рәүештә Больцано, Грассман һәм Ганкель билдәләмә бирәләр[46]. «Элементар математика энциклопедияһы» натураль һандарҙы ҡабатлауға түбәндәге билдәләмәне тәҡдим итә[48]:
|
Билдәләмә. Натураль һандарҙы ҡабатлау тип, һәр һәм натураль һандар парына түбәндәге үҙсәнлектәргә эйә булған бер һәм тик бер генә (йәки ) натураль һанын ярашлы ҡуйған ярашлыҡ атала:
|
Натураль һандарҙы ҡабатлау һәр ваҡыт үтәлеүсән һәм бер мәғәнәле[48].
1891 йылда Пеано натураль һандар өсөн аксиомалар (башҡа сығанаҡтарҙа шулай уҡ 1889 йыл телгә алына) тәҡдим итә[11][46]. Шул ваҡыттан алып аксиомалар бик әҙ генә үҙгәреш кисерәләр.
|
Билдәләмә. Натураль һандар тип, буш булмаған күмәклегенең, ундағы ниндәйҙер һәм элементтары өсөн « » артынан килә бәйләнеше булған, уның өсөн түбәндәге аксиомалар үтәлгән элементтары аталалар[49]:
|
Бөтөн һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]«Элементар математика энциклопедияһы» натураль һандарҙы алыуға түбәндәге билдәләмәне тәҡдим итә[50]:
|
Билдәләмә. Натураль һандарҙы алыу тип, һәр һәм натураль һандар парына, түбәндәге үҙсәнлеккә эйә булған һанын ярашлы ҡуйған ярашлыҡ атала:
|
Натураль һандарҙы алыу булғанда ғына үтәлеүсән, әгәр айырма булһа, ул берҙән бер[50]. Натураль һандарҙы ҡушыу һәм алыу үҙсәнлектәре иҫәбенә киңәйтеү бөтөн һандар төшөнсәһенә килтерә[51].
|
Билдәләмә. Бөтөн һандар ҡулсаһы тип, бөтә натураль һандар күмәклеге ингән һәм түбәндәге үҙсәнлектәргә эйә булған минималь ҡулсаһы атала[52]:
ҡулсаһының элементтары бөтөн һандар тип аталалар. |
ҡулсаһы бар һәм изоморфизмға тиклем теүәллек менән берҙән-бер, ә уның һәр элементы натураль һандарҙың айырмаһына тигеҙ. Ҡулса төҙөгәндә күренешендәге натураль һандар парын ҡулланалар. Парҙар өсөн эквивалентлыҡ, ҡушыу һәм ҡабатлау түбәндәгесә билдәләнә[52]:
- -ға эквивалентлы шул саҡта һәм бары тик шул саҡта ғына, әгәр булһа
Рациональ һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]«Элементар математика энциклопедияһы» натураль һандарҙы бүлеүгә түбәндәге билдәләмәне тәҡдим итә[50]:
|
Билдәләмә. Натураль һандарҙы бүлеү тип, һәр һәм натураль һандар парына түбәндәге үҙсәнлектәргә эйә булған һанын ярашлы ҡуйған ярашлыҡ атала:
|
Натураль һандарҙы бүлеү, ( -ға бүленә) булған осраҡта ғына үтәлеүсән, әгәр бүлендек булһа, ул берҙән бер[50]. Бөтөн һандарҙы ҡабатлау һәм бүлеү төшөнсәләре иҫәбенә киңәйтеү рациональ һандар билдәләмәһенә килтерә[51]. 1710 йылда уҡ Вольф бөтөн һандар менән арифметик ғәмәлдәрҙе башҡарыуҙың билдәле булған закондары кәсерҙәр өсөн туранан-тура ҡулланыла алмайҙар һәм нигеҙләү талап итәләр тигән талап әйтеп бирә. Нигеҙләү үҙе тик XIX быуатта формаль закондарҙың даимилыҡ принцибын ҡулланып эшләнә[53].
|
Билдәләмә. Рациональ һандар яланы тип, бөтөн һандар ҡулсаһы ингән һәм түбәндәге үҙсәнлектәргә эйә булған минималь яланы атала[25]:
яланының элементтары рациональ һандар тип аталалар. |
яланы бар һәм изоморфизмға тиклем аныҡлыҡ менән берҙән бер, ә уның һәр элементы бөтөн һандарҙың бүлендегенә тигеҙ. Бөтөн һандар кеүек үк, рациональ һандар яланын төҙөгәндә парҙары күмәклеген ҡулланалар, ләкин хәҙер инде бөтөн һандарҙың, шул уҡ ваҡытта . Парҙар өсөн эквивалентлыҡ, ҡушыу һәм ҡабатлауҙы түбәндәгесә билдәләйҙәр[25]:
- эквивалентлы шул саҡта һәм тик шул саҡта ғына, әгәр булһа,
Ысын һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]XIX быуаттың икенсе яртыһында ысын һандарҙың төрлө өс теоретик төҙөлөшө тәҡдим ителә. Дедекиндтың тәҡдиме иң популяры була. Кантор үҙенең төҙөлөшөндә сикләнмәләр теорияһын ҡуллана[54].
|
Билдәләмә. Ысын һандар яланы тип, аҫяланы сифатында рациональ һандар яланы ингән өҙлөкһөҙ яланы атала. яланының элементтары ысын һандар тип аталалар[55]. |
яланы бар һәм изоморфизмға тиклем аныҡлыҡ менән берҙән-бер, уның һәр элементы рациональ һандар эҙмә-эҙлелегенең сикләнмәһенә тигеҙ[55].
Комплекслы һандар
[үҙгәртергә | сығанаҡты үҙгәртеү]|
Билдәләмә. Комплекслы һандар яланы тип, ысын һандар яланы һәм шундай элементы, бында ингән, түбәндәге үҙсәнлектәргә эйә булған минималь яланы атала[56]:
яланының элементтары комплекслы һандар тип аталалар. |
яланы алгебраик йомоҡ. Комплекслы һандар яланын төҙөгәндә тәртипкә килтерелгән парҙар күмәклеген ҡулланалар. Парҙар өсөн эквивалентлыҡ, ҡушыу һәм ҡабатлауҙы түбәндәгесә билдәләйҙәр:
- эквивалентлы -ға шул саҡта һәм тик шул саҡта ғына, әгәр һәм булһа,
Формаль арифметика
[үҙгәртергә | сығанаҡты үҙгәртеү]Логик-математик төҙөлөш формаль арифметика тип атала[57]. Логикаға күсеү Гильберт мәктәбенең ҡарашы менән бәйле, ул һандар урынына абстракциялар ҡарай һәм улар өсөн төп арифметик закондар дөрөҫ тип уйлай[20]. Арифметиканы нигеҙләү өсөн аксиоматиканың бер нисә варианты тәҡдим ителә. Ҡушыу һәм ҡабатлау билдәләнгән Пеано аксиомалар системаһынан тыш, Пресбургер аксиомалар системаһы бар, унда тик ҡушыу билдәләнгән, шулай уҡ ҡушыу, ҡабатлау һәм дәрәжәгә күтәреү билдәләнгән аксиомалар. Йыш ҡына аксиомалар сифатында операцияларҙың бөтә үҙсәнлектәрен индерәләр[58][59]. Бөтә был аксиоматик теориялар бөтөн һандар күмәклегенә нигеҙләнгәндәр һәм күмәклектәр теорияһы парадоксын үҙ эсенә алмайҙар. Башҡа тикшеренеү ҡараштары арифметиканы күмәклектәр теорияһы аксиомаларынан йәки математик логиканан ситкә алып сыға[44]. Тикшереү уңайлы булһын өсөн аксиомаларҙы математик логиканың махсус формаль телендә яҙалар[57]. Уға , һанлы үҙгәреүсәндәр, () символдары һәм логик бәйләүестәр () инә, постулаттар булып иҫәпләмә предикаттары постулаттары тора[2]. Индукция аксиомаһы бер ниндәй сикле күмәклек менән алмаштырып булмаған сикһеҙ аксиомалар йыйылмаһынан ғибәрәт[57].
Төп аксиомалар йыйылмаһы өс сифатҡа эйә булырға тейеш[11]:
- ҡапма ҡаршылыҡһыҙ — аксиомалар бер береһе менән конфликтҡа инмәҫкә тейеш;
- бәйләнешһеҙлек — аксиомалар араһында, башҡа аксиомаларҙан логик сығарып булған, артыҡ аксиомалар булырға тейеш түгел;
- тулылыҡ — аксиомалар йыйылмаһы, теләһә ниндәй дөрөҫ әйтелгән теореманы иҫбатларға йәки инҡар итергә мөмкин булһын өсөн етерлек булырға тейеш.
Натураль һандар арифметикаһы математик теорияларҙы нигеҙләү өсөн ҙур әһәмиәткә эйә: уның ҡаршылыҡһыҙ булыуынан ысын һандар арифметикаһының ҡаршылыҡһыҙ булыуы килеп сыға, ул үҙ сиратында, моделдәр ысулын ҡулланып, Евклид геометрияһының һәм Лобачевский геометрияһының ҡаршылыҡһыҙ булыуын күрһәтергә мөмкинлек бирә[11][44]. XX быуат башында Гильберт Пеано системаһында һәм уға туғандаш аксиоматик системаларҙа арифметиканың ҡаршылыҡһыҙ булыуын иҫбатлау менән һөҙөмтәһеҙ шөғөлләнә. 1930 йылда тулы булмау тураһында Гёдель теоремаһын асҡандан һуң, бындай ябай системаларҙа был мөмкин булмауы асыҡ күренә. Ҡаршылыҡһыҙ булыуҙы 1936 йылда Генцен трансфинит индукция төрөн ҡулланып иҫбатлай[57].
Бәйләнешһеҙлеген тикшереү өсөн һәр аксиома сират буйынса ҡапма ҡаршы аксиомаға алмаштырыла һәм килеп сыҡҡан аксиомалар йыйылмаһы үтәлгән модель төҙөлә. Әгәр алмаштырылған аксиома бәйле булһа, йәғни башҡа аксиомаларҙан логик сығарып булһа, ул саҡта уны ҡапма-ҡаршыһына алмаштырыу, һис шикһеҙ, ҡаршылыҡлы аксиомалар системаһына килтерә, һәм моделде төҙөү мөмкин түгел. Шулай итеп, әгәр модель төҙөп булһа, ул саҡта ярашлы аксиома бәйләнешһеҙ була[60]. Ошо ысул менән Пеаноның бөтә аксиомаларының да бер береһенә бәйләнешһеҙ булыуы иҫбат ителә[61].
Пеано аксиомаларында төҙөлгән формаль арифметика саралары менән һандар теорияһының, математик анализ сараларын ҡулланмайынса иҫбатлап була торған теоремаларын, шулай уҡ рекурсив функцияларҙы һәм уларҙың үҙсәнлектәрен яҙып була[2]. Ул Цермело — Френкелдың сикһеҙлек аксиомаһынан тыш аксиоматик күмәклектәр теорияһына эквивалентнлы. Шуның менән бергә 1929 йылда иҫбат ителгән Тулылыҡ тураһында Гёдель теоремаһы Пеано аксиоматикаһы тулы түгел икәнен күрһәтә, йәғни иҫбатлап та, инҡар итеп тә булмаған арифметик теоремалар бар. Арифметика күренешендәге формулаларға ҡарата тулы булған бер ваҡытта, күренешендә теоремалар бар, улар дөрөҫ фекерҙе сағылдыралар, ләкин уларҙы килтереп сығарып булмай[57]. Теоремаларҙың конкрет миҫалдарын табып була: Гудстейн теоремаһы, Парис–Харрингтон теоремаһы һәм башҡалар.
Тарихи очерк
[үҙгәртергә | сығанаҡты үҙгәртеү]Боронғо математик текстар һәм иҫәпләү системалары
[үҙгәртергә | сығанаҡты үҙгәртеү]
Мысыр математик текстары мәсьәләләрҙе сығарыу ысулдары күбеһенсә уларға бәйле булған иҫәпләүҙәргә һәм был осраҡта тыуған ҡыйынлыҡтарға айырым иғтибар бүлгәндәр. Боронғо Мысырҙың математик папирустары уҡыу маҡсатында төҙөлгән булғандар[62], уларҙа сығарылышы менән бергә мәсьәләләр, ярҙамсы таблицалар, бөтөн һандар һәм кәсерҙәр өҫтөндә ғәмәл ҡағиҙәләре бар, арифметик һәм геометрик прогрессиялар, шулай уҡ тигеҙләмәләр осрайҙар[11]. Мысырлылар унарлы иҫәпләү системаһын файҙаланғандар[63]. Мысырлылар шулай уҡ ҡушыу, икеләтеү һәм кәсерҙе берәмеккә тиклем тултырыу кеүек арифметик операцияларҙы белгәндәр. Теләһә ниндәй бөтөн һанға ҡабатлау һәм ҡалдыҡһыҙ бүлеүҙе икеләтеү операцияһын күп тапҡыр ҡабатлау ярҙамында башҡарғандар, был ҙур күләмле иҫәпләүҙәргә килтергән, уларҙа эҙмә-эҙлелегенең билдәле бер быуындары ҡатнашҡан[15]. Мысырҙа тик аликвот кәсерҙәр (1 n {\displaystyle {\frac {1}{n}}} {\frac {1}{n}} күренешендәге кәсерҙәр), йәки берәмектең өлөштәре () ҡулланылған, ә бөтә ҡалған кәсерҙәр аликвот кәсерҙәрҙең суммаһына тарҡатылған[64]. Квадраттың майҙанын, кубтың күләмен йәки майҙаны буйынса квадраттың яғын тапҡанда, был операцияларҙың әлегә исемдәре булмаһа ла, мысырлылар дәрәжәгә күтәреүгә һәм тамыр алыуға юлыҡҡандар[15].

Вавилон шына яҙыулы математик текстар шумерҙар өсөн характерлы булған алтмышарлы иҫәпләү системаһын ҡулланғандар[65], һәм -ҙән алып -ға тиклем һандар өсөн ҡабатлау таблицалары, шулай уҡ кире һандар таблицалары, натураль рәт һандарының квадраттары һәм кубтары таблицалары, проценттарҙы иҫәпләү таблицалары, нигеҙе менән кәсерҙәр ингән уҡыу әсбабтарынан ғибәрәттәр[11][63]. Арифметик мәсьәләләрҙе сығарғанда вавилонлылар пропорцияларға һәм прогрессияларға таянғандар. Улар арифметик прогрессияның быуынының суммаһы формулаһын, геометрик прогрессияның суммаһын табыу ҡағиҙәләрен белгәндәр, процентҡа мәсьәләләр эшләгәндәр[66]. Вавилонда күп пифагор өсәүен белгәндәр, моғайын уларҙы эҙләү өсөн билдәһеҙ дөйөм ысул менән файҙаланғандарҙыр. Дөйөм алғанда, тигеҙләмәһенең бөтөн һәм рациональ сығарылыштарын табыу мәсьәләһе һандар теорияһына ҡарай[67]. Геометрик мәсьәләләр яҡынса квадрат тамырҙар алыу кәрәклегенә килтерә, уларҙы ҡағиҙәһен һәм һөҙөмтәгә артабан яҡынлау өсөн итерацион ысулдар ҡулланып башҡарғандар[ком. 1].

Боронғо мысыр математик текстары б. э. тиклем XIV—VII быуаттарға ҡарайҙар [69] Тәү башта мысырлылар аттик нумерация менән файҙаланғандар, уны ваҡыт үтеү менән компактлы хәрефле, йәки Мысыр иҫәпләү системаһы алмаштыра [70]. Боронғо Мысыр арифметикаһының үҫеше пифагорсылар мәктәбенеке һанала. Пифагорсылар тәүҙә теләһә ниндәй ике киҫектең сағыштырмаһын бөтөн һандарҙың сағыштырмаһы аша күрһәтергә мөмкин, йәғни геометрия рациональ һандар арифметикаһынан ғибәрәт тип уйлағандар. Улар тик бөтөн ыңғай һандарҙы ҡарағандар һәм һанды берәмектәр йыйынтығы тип билдәләгәндәр. Һандарҙың үҙсәнлектәрен өйрәнеп, уларҙы йоп һәм таҡ (икегә бүленеүсәнлек билдәһе һымаҡ), ябай һәм ҡушма һандарға бүлгәндәр, сикһеҙ күп пифагор өслөләрен белгәндәр[71]. Б. э. тиклем 399 йылда бүленеүсәнлектең дөйөм теорияһы барлыҡҡа килә, ул Сократтың уҡыусыһы Теэтеттыҡы һанала. Евклид «Башланғыстарҙың» VII китабын һәм IX китаптың бер өлөшөн шуға арнаған. Теорияның нигеҙендә ике һандың иң ҙур уртаҡ бүлеүсеһен табыу өсөн Евклид алгоритмы ята. Теләһә ниндәй һанды ябай ҡабатлашыусыларға тарҡатыу мөмкинлеге һәм бындай тарҡатыуҙың берҙән берлеге алгоритмдың эҙемтәһе булып тора[72].
Шуның менән бергә берәмек квадраттың диагоналы һәм яғы үлсәүҙәш булмауын пифагорсылар иҫбатлаған тип һанала. Был асыш бөтөн һандарҙың сағыштырмаһы теләһә ниндәй киҫектәрҙең сағыштырмаһын күрһәтеү өсөн етерлек түгел, һәм шуның нигеҙендә метрик геометрияны төҙөү мөмкин түгел тигәнде аңлата[73]. Иррационаллек тураһында тәүге ғилем Теэтеттыҡы тип иҫәпләнә. Евклид алгоритмы рациональ һанды өҙлөкһөҙ кәсергә тарҡатыуҙың тулы булмаған бүлендеген табырға ярҙам итә. Шуның менән бергә өҙлөкһөҙ кәсер төшөнсәһе Боронғо Мысырҙа булмай[72]. III быуатта Диофант алгебраны арифметикаға түгел, ә геометрияға таянып төҙөй башлай. Диофант шулай уҡ һандар өлкәһен тиҫкәре һандарға киңәйтә[74].
Рим нумерация системаһы иҫәпләүҙәр өсөн әҙ ҡулайлы була. Рим һан тамғалары алфавит барлыҡҡа килгәнгә тиклем үк барлыҡҡа килгәндәр һәм уның хәрефтәренән килеп сыҡмағандар. Беренсе башлап -ҙән алып -ға тиклем һандар вертикаль һыҙыҡтар һаны менән тамғаланған тип иҫәпләнә, ә уларҙы һыҙыу һанды унлатыуҙы аңлатҡан ( һаны шунан килеп сыҡҡан). Ярашлы рәүештә, һаны килеп сыҡһын өсөн, таяҡты ике тапҡыр сыйғандар. Аҙағыраҡ система ябайлаша[75]. Хәҙерге ваҡытта ул башлыса тәртип һандарын тамғалау өсөн ҡулланыла.
XIV быуатҡа тиклем Ҡытай математикаһы иҫәпләү таҡтаһында сығарыу өсөн иҫәпләү алгоритмдары йыйылмаһынан ғибәрәт булған [76]. Иҫәпләү таҡтаһында башҡарылған ҡушыу һәм алыу арифметик операциялары өҫтәлмә таблицалар талап итмәгән, ҡабатлау өсөн -ҙән алып -ға тиклем таблица булған. Ҡабатлау һәм бүлеү ғәмәлдәре өлкән разрядтарҙан башлап башҡарылған, был ваҡытта аралағы һөҙөмтәләр таҡтанан юйылған, шул арҡала дөрөҫлөгөн тикшереү мөмкин булмаған. Башта ҡабатлау һәм бүлеү бәйһеҙ ғәмәлдәр булалар, ләкин аҙаҡ Сунь Цзы уларҙың үҙ-ара кире булыуына иғтибар иткән[77]. Ҡытайҙа ике ялған фекер ҡағиҙәһе ярҙамында мәсьәлә сығара белгәндәр[78], ә Һыҙыҡлы тигеҙләмәләр системаһын сығарыу өсөн тиҫкәре һандар индәргәндәр. Тәүҙә улар тик иҫәпләү процесында ҡулланылғандар һәм иҫәпләү аҙағында таҡтанан юйылғандар, аҙаҡ ҡытай ғалимдары уларға бурыс йәки тулмау тигән мәғәнә биргәндәр[79].
Урта быуаттарҙа арифметика
[үҙгәртергә | сығанаҡты үҙгәртеү]
Позицион иҫәпләү системаһы (нолде лә индереп ун цифр) Һиндостанда индерелә. Ул арифметик операцияларҙы башҡарыуҙың сағыштырмаса ябай ҡағиҙәләрен эшләргә мөмкинлек бирә[11]. Һиндостанда төп арифметик ғәмәлдәр тип ҡушыу, алыу, ҡабатлау, бүлеү, дәрәжәгә күтәреү һәм куб, квадрат һәм куб тамырҙар алыу һанала, улар өсөн ҡағиҙәләр эшләнә. Иҫәпләүҙәр ҡомло йәки туҙанлы таҡтала йәки ерҙә башҡарыла һәм таяҡ менән яҙыла[80]. Һиндтар кәсерҙәрҙе белгәндәр һәм улар өҫтөндә ғәмәлдәр башҡарғандар, пропорцияларҙы, прогрессияларҙы белгәндәр[81]. Б. э. VII быуатында уҡ тиҫкәре һандар менән эш иткәндәр, уларҙы бурыс тип аңлатҡандар, шулай уҡ иррациональ һандарҙы ҡулланғандар[82].

IX быуат башында Әбү Ғабдулла Мөхәммәт ибн Муса әл-Хәрәзми «Һинд иҫәбе тураһында» тигән китап яҙған. Дәреслеккә «төрлө төрҙәге һәм сорттағы» практик мәсьәләләрҙең сығарылышы ингән һәм ул позицион иҫәпләү системаһын ҡулланып яҙылған беренсе китап була, быға тиклем цифрҙарҙы иҫәпләү таҡтаһында иҫәпләүҙәр башҡарыу өсөн генә ҡулланған булғандар[83][84]. XII быуатта Аделард һәм Иоанн Севельский тарафынан китаптың латин теленә ике тәржемәһе эшләнгән[85]. Уның оригиналы һаҡланмаған, ләкин 1857 йылда «әл-Хәрәзми һинд һаны тураһында» исеме аҫтында табылған латин теленә тәржемәһе баҫылып сыҡҡан[83]. Трактатта һинд цифрҙары ярҙамында иҫәпләү таҡтаһында ҡушыу, алыу, икеләтеү, ҡабатлау, икегә бүлеү, бүлеү һәм квадрат тамыр алыу кеүек арифметик ғәмәлдәрҙе башҡарыу һүрәтләнә[86]. Кәсерҙәрҙе ҡабатлау, бүлеү кеүек үк, пропорциялар ярҙамында ҡарала: -ны -ға ҡабатлау үтәлгән һанын эҙләүгә тиң булған. Был теория ғәрәп арифметикаһының нигеҙе булған. Әммә шуның менән бергә, теләһә ниндәй кәсерҙе аликвот кәсерҙәр суммаһы күренешендә күрһәтеүсе, кәсерҙәрҙең икенсе иҫәпләмәһе лә булған[87]. Мәсьәләләр эшләү өсөн ғәрәптәр, Һиндостандан килгән һәм бер нисә башҡа ысулдар менән бер рәттән Әл-Бируниҙың «Об индийских рашиках» китабында тасуирланған өсләтә ҡағиҙә менән, Ҡытайҙан килгән һәм Куста ибн Лукканың «Книга о правиле двойного ложного положения» китабында теоретик нигеҙләнгән ике ялған фекер ҡағиҙәһе менән файҙаланғандар[88].
Испания һәм Сицилия аша X быуатта Европаның ғәрәп донъяһы менән фәнни бәйләнештәре үҫешә башлай. Ошо ваҡытта һуңғараҡ папа Сильвестр II булып киткән ғалим монах Герберт Каталонияға килә. «Книжка о делении чисел» һәм «Правила счёта на абаке» яҙмаларын уныҡы тип иҫәпләйҙәр. Ике китабында ла һандар һүҙҙәр йәки рим цифрҙары менән яҙылған[89]. Герберт абакта иҫәпләүселәрҙе «абацистар» тип атай. XII—XIII быуаттарҙа Европала арифметика буйынса ғәрәп китаптарының тәржемәләре күренә башлай. Китаптарҙа килтерелгән унарлы позицион нумерация яҡлылар ғәрәп математигы әл-Хәрәзмиҙың латинса исеме буйынса «әлгористар» тип аталалар[90]. XIII быуат башында Көнбайыш Европала ике иҫәпләү системаһы була: абакка нигеҙләнгән һәм Герберт тарафынан хупланған иҫке, һәм яңы, Леонардо Фибоначчи тарафынан хупланған позицион һинд системаһы. Яйлап яңы система өҫтөнлөк ала[85][91]. Уның төп өҫтөнлөгө булып арифметик операцияларҙың ябайлашыуы тоа. Шуның менән бергә Германияла, Францияла һәм Англияла XV быуат аҙағына тиклем яңы цифрҙар ҡулланылмай. Иҫке нумерация тик XVI—XVII быуаттарҙа тулыһынса ҡыҫырыҡлап сығарыла[91].
1427 йылда әл-Каши унарлы кәсерҙәр системаһын тасуирлай, ул Стевиндың 1585 йылдағы хеҙмәттәренән һуң киң таралыу ала[11]. Стевин унарлы системаны мөмкин тиклем киңерәк таратырға теләй. Тап шуның өсөн ул үҙенең хеҙмәттәрен латин телендә түгел, ә француз һәм фламанд телдәрендә яҙа. Бынан тыш, ул унарлы үлсәүҙәр системаһын индереүҙе яҡлап көрәшеүсе булып китә[37].
Яңы осор арифметикаһы
[үҙгәртергә | сығанаҡты үҙгәртеү]
XVII быуатта диңгеҙҙә йөҙөү астрономияһы, механика, ҡатмарлыраҡ коммерция иҫәп-хисабы арифметика алдына иҫәпләү техникаһына яңы бурыстар ҡуя һәм уның артабанғы үҫешенә этәргес бирә. Һан төшөнсәһе ҙур үҙгәреш кисерә. Әгәр элек һандар өлкәһенә күбеһенсә тик ыңғай рациональ һандарҙы индерһәләр, XVI быуат башынан иррациональ һәм тиҫкәре һандар нығыраҡ танылыу алалар. Ньютон үҙенең лекцияларында һандарҙы өс төргә бүлә: бөтөн (берәмек менән үлсәнәләр), кәсер (берәмек өлөшө бүленеүселәре) һәм иррациональ һандар (берәмек менән үлсәүҙәш түгел). 1710 йылдан башлап һандың был билдәләмәһе бөтә дәреслектәргә ныҡлы үтеп инә[92].
XVII быуат башында Непер логарифмдарҙы уйлап таба. Логарифмдарҙы һәм унарлы кәсерҙәрҙе ҡулланыу, арифметикаға рациональ яҡынайыуҙар эҙмә-эҙлелеге булараҡ иррациональ һан төшөнсәһен индереү XVII быуат аҙағына арифметиканың ҡулланыу өлкәһен киңәйтә һәм өҙлөкһөҙ дәүмәлдәрҙе өйрәнеү өсөн фәндең фундаменталь әһәмиәтен билдәләй[11].
Математиканың нигеҙҙәрен тәнҡит күҙлегенән ҡайтанан ҡарау Лобачевскийҙың геометрияһы менән бәйле, был XIX быуатта була. XVIII быуатта уҡ әле һан төшөнсәһен теоретик нигеҙләргә маташыуҙар башлана. Лейбниц беренсе булып арифметиканы дедуктив төҙөү бурысын ҡуя, атап әйткәндә, 1705 йылда үҙенең «Новые опыты о человеческом разуме» хеҙмәтендә «ике плюс ике тигеҙ дүрткә» тигеҙлеген иҫбатлау кәрәклеген күрһәтә. Был мәсьәләне хәл итергә маташып Вольф 1770 йылда, Шульц — 1790 йылда, Ом — 1822 йылдау, Грассман — 1861 йылда һәм, нимәйәт, Пеано — 1889 йылда үҙҙәренең аксималарын тәҡдим итәләр[93].
1758 йылда Кестнер «Арифметиканың, геометрияның, яҫы һәм сферик тригонометрияның тәүге нигеҙҙәре һәм перспективалары» хеҙмәтендә бөтә арифметик төшөнсәләрҙе бөтөн һан аша нигеҙләргә саҡыра. Шулай итеп ул, китаптағы тәртиптә, натураль һандарҙы, кәсерҙәрҙе, тиҫкәре һандарҙы, унарлы кәсерҙәрҙе, иррациональ һандарҙы һәм шунан һуң ғына бәйләнештәр теорияһын билдәләй[94]. Тиҫкәре һандар теорияһын төҙөгәндә, тиҫкәре һан нулдән бәләкәй, йәғни, бер нәмә лә булмағандан да бәләкәй тигән раҫлау төп проблема булып тора[95].
Каспаром Вессель 1799 йылда «Опыт об аналитическом представлении направления и его применениях, преимущественно к решению плоских и сферических многоугольников» хеҙмәтендәе комплекслы һандарға тулыһынса геометрик аңлатма тәҡдим итә. Вессель теорияны өс үлсәмле арауыҡҡа дөйөмләштерергә маташа, ләкин был барып сыҡмай. Гамильтон ҡабатлағанда коммутативлыҡ законы үтәлмәгән кватерниондар теорияһын төҙөгәнгә тиклем был мәсьәлә асыҡ ҡала. Шуның менән бергә Вейерштрастың, Фробениустың һәм Пирстың тикшеренеүҙәренән, һан төшөнсәһен комплекслы һандарҙан тышҡа киңәйткәндә ниндәй ҙә булһа арифметик закондан баш тартырға тура килә икәне күренә [96].
Арифметика мәғарифта
[үҙгәртергә | сығанаҡты үҙгәртеү]Арифметик төшөнсәләрҙең барлыҡҡа килеүе иҫәпләү процесы менән тығыҙ бәйләнгән. Уның нигеҙендә фекерләү эшмәкәрлегенең предметты таный белеү; предметтарҙы айыра белеү; предметтар йыйылмаһын элементтарға айырыу, иҫәпләүҙә тиң хоҡуҡлылар (икенсе төрлө әйткәндә, иҫәпләү берәмеге менән ҡулланыу); элементтарҙы эҙмә-эҙ урынлаштыра белеү, уларҙы тәртипкә килтереү кеүек элементтары ята, был сифаты буйынса төрлө предметтарҙы иҫәпләүгә һәм һан төшөнсәһе барлыҡҡа килеүгә килтерә. Балалар менән төшөнсәне өйрәнгәндә ошондай процестарҙы күҙәтергә мөмкин[11].
Итак, какую же из дисциплин нужно изучать первой, если не ту, что является началом и выполняет как бы роль матери по отношению к другим [дисциплинам]? Такова как раз арифметика. Она предшествует всем другим не только потому, что сам Бог, творец этого мироздания, взял её первой за образец своего мыслеполагания и по её [принципу] устроил всё, что через числа силой творящего Разума обрело гармонию в установленном порядке, но и потому арифметика объявляется предшествующей, что если устранить предшествующие по своей природе сущности, тотчас же устраняются и последующие. Если гибнут последующие, то ничего в статусе предыдущей субстанции не меняется.
Башланғыс белем биреү стандарттары һандарҙы миллионға тиклем иҫәпләй һәм сағыштыра белеү күнекмәһен, төп үлсәү берәмектәре һәм улар араһындағы нисбәт менән эш итә белеүҙе, төп дүрт арифметик операцияны башҡара белеүҙе (телдән 100-гә тиклем һәм яҙма 10 000-гә тиклем), шулай уҡ ҡалдыҡлы бүлеүҙе, бер нисә арифметик ғәмәлдән торған һанлы аңлатманың ҡиммәтен таба белеүҙе талап итә[98][99]. Мәктәп материалы күргәҙмә күҙаллауҙар ярҙамында бирелә. Беренсе класта балалар һан образдары һәм предметтар һаны менән эш итәләр, иҫәп 20-гә тиклем. Икенсе класта унарлы системаны, позицион системаны, ҡабатлау таблицаһын индерәләр, иҫәп 100-гә тиклем. Өсөнсө класта күп урынлы һандар менән арифметик ғәмәлдәрҙе индәрәләр. Артабанғы аҙым булып хәрефле тамғалауҙарға, икенсе төрлө әйткәндә — билдәленән абстрактлыға күсеү тора. Клейндың фекеренсә, тап ошонан математика башлана[100]. Башланғыс мәктәптә арифметиканы өйрәнеүҙең ҡыйынлығы предметтарҙың тәбиғәтенән ситләштерелгән иҫәп башҡарырға кәрәк булыуында[101].
Урта мәктәптә уҡытыу һан төшөнсәһен киңәйтеү менән бәйле, кәсерҙәр һәм улар өҫтөндә ғәмәлдәр, тиҫкәре һандар, иррациональ һандар индерелә[102]. Ысын һәм комплекслы һандар, шулай уҡ Евклид алгоритмы һәм арифметиканың төп теоремаһы тулы урта белемгә инә. Рәсәй Федераль дәүләт белем биреү стандартына ярашлы, ««Арифметика» бүлегенең йөкмәткеһе уҡыусылар тарафынан математиканы артабан өйрәнеү өсөн нигеҙ булып тора, һәм уларҙың логик фекерләүе үҫешенә, алгоритмдар менән файҙалана белеүҙәрен формалаштырырға, шулай уҡ көндәлек тормошта кәрәк булған практик күнекмәләргә эйә булырға булышлыҡ итә»[103].
Хәҙерге донъяла математик грамоталылыҡ белем биреүҙең төп маҡсаттарының береһе булып тора. Ул үҙ эсенә, атап әйткәндә, арифметик ғәмәлдәрҙе башҡара белеүҙе, иҫәп-хисап һәм үлсәүҙәр башҡарыуҙы индерә[104]. Балаларҙың һәм ололарҙың математик грамоталылыҡ мәсьәләләре менән ЮНИСЕФ һәм ЮНЕСКО кеүек ойошмалар шөғөлләнә[105][106].
Шуның менән бергә арифметик ғәмәлдәргә өйрәтеү оҙаҡ ваҡыт өлгө буйынса механик башҡарыуға ҡайтып ҡалды. Боронғо Ҡытайҙа математиканы уҡытыуға, экзамендар биреүҙе лә индереп, ҙур иғтибар бүленә. Император академияһында математика ете йыл өйрәнелә. Ләкин классик математик трактаттарға догма һымаҡ ҡарайҙар һәм яңынан үҙгәрешһеҙ баҫтырып сығарылалар[107].
Европала XVI быуатта Тарталья тарафынан ҡушыуға, алыуға, ҡабатлауға һәм бүлеүгә систематик күнегеүҙәр тәҡдим ителә, ләкин улар әле оҙаҡ ваҡыт ҡулланылышҡа инмәйҙәр[108]. Бынан тыш, Урта быуаттарҙа күп һандағы айырым арифметик мәсьәләләрҙе сығарыу өсөн ҡағиҙәләр була. Ҡайһы бер дәреслектәрҙә 26-ға тиклем шундай ҡағиҙәләр осрай, шуның менән бергә улар дәреслектән дәреслеккә тап килмәҫкә мөмкиндәр[109]. Ҡайһы бер ҡағиҙәләр әле лә үҙҙәренең актуаллеген юғалтмағандар. Уларға пропорцияларҙы (кәсерҙәрҙе ике һандың сағыштырмаһы итеп ҡарағандар, был ғәмәлдәрҙе башҡарыу өсөн пропорцияларҙы ҡарауға килтергән), проценттарҙы индәрәләр[110].
Арифметика уҡытыу кимәле буйынса ете ирекле сәнғәттең дүртенсеһе булып тора. Унан алда Грамматиканан, Риториканан һәм Диалектиканан торған тривиум, ә ул үҙе квадривиумда юғары фән булып тора, уға шулай уҡ Геометрия, Музыка һәм Астрономия инә[111]. Тәүге Европа университеттары барлыҡҡа килгәс математика сәнғәт факультеттарында квадривиум булараҡ уҡытыла һәм ярҙамсы фән була. Арифметика буйынса беренсе лекцияларҙы 1412 йылда Вена университеты магистры Иоганн Гмунден уҡый[112].
Арифметика философияла һәм сәнғәттә
[үҙгәртергә | сығанаҡты үҙгәртеү]
Пифагорcылар бөтөн һандарҙың сағыштырмаһын киҫектәрҙең геометрик сағыштырмаһы, шулай уҡ гармонияла һәм музыкала аналогик сағыштырмалар өсөн ҡулланғандан һуң, улар ғаләмдың бөтә законлыҡтарын һандар ярҙамында тасуирлап була, ә арифметика сағыштырмаларҙы күрһәтеү һәм донъяның моделен төҙөү өсөн кәрәк тигән фекергә киләләр[113]. Шуның менән бергә, бөтөн һандарҙың сағыштырмалары теләһә ниндәй киҫектәрҙең сағыштырмаһын күрһәтеү өсөн етерлек түгел (квадраттың яғы һәм диагонале үлсәүҙәш түгел) һәм шул арҡала метрик геометрияны төҙөү мөмкин түгел икәне пифагорсыларҙың асыштарының береһе булып тора[73]. Сикле үлсәм төҙөү һәм ысын һанды билдәләү проблемалары б. э. тиклем V быуаттың фәнни кризисын асып һала, Боронғо Мысырҙың бөтә философик мәктәптәре ошо проблеманан сығыу юлдарын эҙләү менән шөғөлләнә. Был проблемаларҙы хәл итеүҙә килеп тыуған бөтә ҡыйынлыҡтарҙы Зенон Элейскийгә уның парадокстарында, йәки апорияларында күрһәтергә мөмкин була[114].
Марциан Капелла үҙенең «Свадьба Философии и Меркурия» трактатында бөтә ете сәнғәттең һәм шул иҫәптән Арифметиканың визуаль образдарын тыуҙыра. Сәнғәттәрҙе ярашлы атрибуттары менән ҡатын-ҡыҙҙар кәүҙәләндерәләр, уларҙы сфераның билдәле вәкилдәре оҙатып йөрөй. Арифметика үҙенең ҡулдарына цифрҙар яҙып тултырылған скрижаль (изге яҙма төшөрөлгән таҡта) йәки абак тотҡан. Уны Пифагор оҙатып йөрөй[115].
Иҫәп Будданы һынауҙарҙың береһе була. Уҡтан атыуҙа, йүгереүҙә һәм йөҙөүҙә ярыштарҙан һуң математик Арйюна ҙурыраҡ булған бөтә һанлы дәрәжәләрҙе әйтеп бирергә ҡушҡан. Будда -нә тиклем егерме ике дәрәжәне әйткән (тик таҡ дәрәжәләрҙең генә исемдәре булған), һәм был әле тик беренсе һанау булған, икенсе һанауҙа Будда -гә тиклем дауам иткән. Артабанғы заданиела Будда бер милдәге, ә аҙаҡ ер йөҙөндәге атомдар һанын иҫәпләгән[116]. Шундай «һанлы баҫҡыстар» күп тапҡыр һинд дини шиғриәтендә осрайҙар, шуның менән бергә һандарҙы белдереүсе һүҙҙәр төрлө булырға мөмкиндәр. Бындай баҫҡыстарҙың тәғәйенләнеше — рухи бейеклеккә күтәрелеү. «Лилаватистара» исемле һинд китабында Ер ханымдың, сибәр Гопаның кейәү егеттәре араһында яҙмала, арифметикала, көрәштә һәм уҡ һелтәү сәнғәтендә ярышы һүрәтләнә. Әҫәрҙең күп өлөшө арифметикала ярышҡа арналған[117].
Һиндостандағы кеүек, майя әһелдәре тарафынан яһалма төҙөлгән бик ҙур һандар «һанлы баҫҡыс» буйлап бейегерәккә күтәрелергә, аллаларға яҡынайырға тырышыу тураһында һөйләй[118].
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- Комментарийҙар
- ↑ Пусть необходимо найти корень из , — первое приближение с недостатком, — приближение с избытком. Второе приближение образуется по формуле среднего арифметического , и ему соответствует , и так далее)[68].
- Ҡулланылған әҙәбиәт һәм сығанаҡтар
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 Виноградов И. М. Арифметика // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 1.
- ↑ 2,0 2,1 2,2 2,3 Виноградов И. М. Арифметика формальная // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 1.
- ↑ 3,0 3,1 3,2 3,3 3,4 3,5 3,6 Арифметика, наука // Брокгауз һәм Ефрондың энциклопедик һүҙлеге: 86 томда (82 т. һәм 4 өҫтәмә том). — СПб., 1890—1907. (рус.)
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 4,6 4,7 4,8 MacDuffee C. C. Arithmetic. Encyclopædia Britannica. Дата обращения: 20 март 2012. Архивировано 28 май 2012 года. (инг.)
- ↑ АРИФМЕ́ТИКА. Большая российская энциклопедия. Дата обращения: 15 июнь 2017. 2017 йыл 27 июнь архивланған.
- ↑ Арнольд, 1938, с. 3—5
- ↑ Понтрягин, 1986, с. 4—6
- ↑ Беллюстин В. Глава 12. Число и порядок действий, знаки и определения // Как постепенно дошли люди до настоящей арифметики. — М.: Типография К. Л. Меньшова, 1909.
- ↑ Депман, 1965, с. 195—199
- ↑ Арнольд, 1938, с. 151—156
- ↑ 11,00 11,01 11,02 11,03 11,04 11,05 11,06 11,07 11,08 11,09 11,10 Арифметика. Большая советская энциклопедия. Дата обращения: 20 ғинуар 2013. Архивировано 3 ноябрь 2012 года.
- ↑ Алгебра. Большая советская энциклопедия. Дата обращения: 20 ғинуар 2013. Архивировано 1 февраль 2013 года.
- ↑ Депман, 1965, с. 21—25
- ↑ Депман, 1965, с. 129—130
- ↑ 15,0 15,1 15,2 История математики, т. I, 1970, с. 23—24
- ↑ 16,0 16,1 16,2 16,3 Депман, 1965, с. 212—232
- ↑ 17,0 17,1 17,2 Депман, 1965, с. 204
- ↑ Арифметика, 1951, с. 142
- ↑ Клейн, 1987, с. 23—26
- ↑ 20,0 20,1 20,2 20,3 Клейн, 1987, с. 26—35
- ↑ Арифметика, 1951, с. 77—79
- ↑ Клейн, 1987, с. 37—44
- ↑ Арифметика, 1951, с. 157
- ↑ Клейн, 1987
- ↑ 25,0 25,1 25,2 Арифметика, 1951, с. 172—178
- ↑ Арифметика, 1951, с. 188—201
- ↑ Арифметика, 1951, с. 227
- ↑ Клейн, 1987, с. 35—36
- ↑ 29,0 29,1 Клейн, 1987, с. 23—25
- ↑ Арифметика. Энциклопедия Кольера. Дата обращения: 20 ғинуар 2013. Архивировано 1 февраль 2013 года.
- ↑ 31,0 31,1 Кнут, с. 216
- ↑ История математики, т. II, 1970, с. 66—67
- ↑ История математики, т. III, 1972, с. 42—45
- ↑ Клейн, 1987, с. 45—49
- ↑ Депман, 1965, с. 263—267
- ↑ Boyer & Merzbach, 2010, Arithmetic and logistic
- ↑ 37,0 37,1 Арифметика, 1951, с. 57—71
- ↑ Кнут, с. 216, 221
- ↑ Депман, 1965, с. 275—285
- ↑ Клейн, 1987, с. 49—57
- ↑ 41,0 41,1 41,2 Виноградов И. М. Чисел теория // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 5.
- ↑ Виноградов И. М. Элементарная теория чисел // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 5.
- ↑ Арнольд, 1938, с. 413—415
- ↑ 44,0 44,1 44,2 Аксиоматический метод. Большая советская энциклопедия. Дата обращения: 20 ғинуар 2013. Архивировано 11 февраль 2013 года.
- ↑ Арифметика, 1951, с. 100—107
- ↑ 46,0 46,1 46,2 Депман, 1965, с. 117—126
- ↑ 47,0 47,1 Арифметика, 1951, с. 135—138
- ↑ 48,0 48,1 Арифметика, 1951, с. 139—142
- ↑ Арифметика, 1951, с. 133
- ↑ 50,0 50,1 50,2 50,3 Арифметика, 1951, с. 150—151
- ↑ 51,0 51,1 Арифметика, 1951, с. 172—179
- ↑ 52,0 52,1 Арифметика, 1951, с. 160—167
- ↑ Депман, 1965, с. 258—262
- ↑ Арифметика, 1951, с. 188
- ↑ 55,0 55,1 Арифметика, 1951, с. 202
- ↑ Арифметика, 1951, с. 228
- ↑ 57,0 57,1 57,2 57,3 57,4 Формальная арифметика. Большая советская энциклопедия. Дата обращения: 20 ғинуар 2013. Архивировано 3 ноябрь 2012 года.
- ↑ Avigad, 2003, p. 260
- ↑ Нечаев, 1975, с. 52—53
- ↑ Нечаев, 1975, с. 48
- ↑ Нечаев, 1975, с. 68—72
- ↑ История математики, т. I, 1970, с. 19—20
- ↑ 63,0 63,1 Депман, 1965, с. 49—52
- ↑ История математики, т. I, 1970, с. 25
- ↑ История математики, т. I, 1970, с. 34
- ↑ История математики, т. I, 1970, с. 40
- ↑ История математики, т. I, 1970, с. 50
- ↑ История математики, т. I, 1970, с. 46—47
- ↑ Депман, 1965, с. 53—54
- ↑ История математики, т. I, 1970, с. 62
- ↑ История математики, т. I, 1970, с. 68—69
- ↑ 72,0 72,1 История математики, т. I, 1970, с. 74—76
- ↑ 73,0 73,1 История математики, т. I, 1970, с. 73
- ↑ История математики, т. I, 1970, с. 144—146
- ↑ Депман, 1965, с. 57—58
- ↑ История математики, т. I, 1970, с. 178
- ↑ История математики, т. I, 1970, с. 160—161
- ↑ История математики, т. I, 1970, с. 163—164
- ↑ История математики, т. I, 1970, с. 167—169
- ↑ История математики, т. I, 1970, с. 183—185
- ↑ История математики, т. I, 1970, с. 185
- ↑ История математики, т. I, 1970, с. 190—191
- ↑ 83,0 83,1 Депман, 1965, с. 72—78
- ↑ История математики, т. I, 1970, с. 209—210
- ↑ 85,0 85,1 Депман, 1965, с. 90—94
- ↑ История математики, т. I, 1970, с. 211—212
- ↑ История математики, т. I, 1970, с. 212—214
- ↑ История математики, т. I, 1970, с. 218—219
- ↑ История математики, т. I, 1970, с. 254—256
- ↑ История математики, т. I, 1970, с. 256—257
- ↑ 91,0 91,1 Арифметика, 1951, с. 50—57
- ↑ История математики, т. II, 1970, с. 34—36
- ↑ История математики, т. III, 1972, с. 47—49
- ↑ История математики, т. III, 1972, с. 49—52
- ↑ История математики, т. III, 1972, с. 52—56
- ↑ История математики, т. III, 1972, с. 61—66
- ↑ Боэций. I, 1 // Основы арифметики.
- ↑ Примерная основная образовательная программа образовательного учреждения. Начальная школа. Федеральный государственный образовательный стандарт. Дата обращения: 5 декабрь 2012. Архивировано 7 декабрь 2012 года. 2012 йыл 30 октябрь архивланған.
- ↑ Примерная основная образовательная программа образовательного учреждения. Начальная школа / сост. Е. С. Савинов. — 4-е. — М.: Просвещение, 2013. — С. 32—35. — 223 с. — ISBN 9785090264167.
- ↑ Клейн, 1987, с. 20—23
- ↑ Депман, 1965, с. 1—3, 103—109
- ↑ Клейн, 1987, с. 37
- ↑ Примерные программы по учебным предметам. Математика. Федеральный государственный образовательный стандарт. Дата обращения: 5 декабрь 2012. Архивировано 7 декабрь 2012 года. 2013 йыл 19 ғинуар архивланған.
- ↑ Грамотность, математические способности и навыки решения задач в технологически развитом обществе. Национальный исследовательский университет Высшая школа экономики. Дата обращения: 5 декабрь 2012. Архивировано 7 декабрь 2012 года. 2013 йыл 7 октябрь архивланған.
- ↑ Defining Quality in Education (ингл.). ЮНИСЕФ. Дата обращения: 5 декабрь 2012. 2012 йыл 15 октябрь архивланған.
- ↑ Education for All Goals (ингл.). ЮНЕСКО. Дата обращения: 5 декабрь 2012. Архивировано 7 декабрь 2012 года.
- ↑ История математики, т. I, 1970, с. 157
- ↑ Депман, 1965, с. 199—203
- ↑ Депман, 1965, с. 305
- ↑ Депман, 1965, с. 306
- ↑ Liberal Arts. Encyclopædia Britannica. Дата обращения: 20 март 2012. Архивировано 28 май 2012 года. (инг.)
- ↑ История математики, т. I, 1970, с. 259—260
- ↑ История математики, т. I, 1970, с. 67
- ↑ История математики, т. I, 1970, с. 88—89
- ↑ Семь свободных искусств. Simbolarium. Дата обращения: 20 март 2012. Архивировано 28 май 2012 года. 2014 йыл 31 август архивланған.
- ↑ Меннингер, 2011, с. 176—179
- ↑ Арифметика, 1951, с. 49
- ↑ Меннингер, 2011, с. 82
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]| арифметика Викиһүҙлектә | |
| Арифметика Викимилектә |
- Арнольд И. В. Теоретическая арифметика. — М.: Государственное учебно-педагогическое издательство, 1938. — 481 с.
- Депман И. Я. История арифметики. — М.: Просвещение, 1965. — 400 с.
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I: Арифметика. Алгебра. Анализ. — 432 с.
- Кнут Д. Э. Арифметика // Искусство программирования. — М. — Т. II. — 830 с.
- Меннингер К. История цифр. Числа, символы, слова. — М.: ЗАО Центрполиграф, 2011. — 543 с. — ISBN 9785952449787.
- Нечаев В. И. Числовые системы. — М.: Просвещение, 1975. — 199 с.
- Понтрягин Л. С. Обобщения чисел. — М.: Наука, 1986. — 120 с. — (Библиотечка «Квант»).
- Серр Ж.-П. Курс арифметики / пер. с франц. А. И. Скопина под ред. А. В. Малышева. — М.: Мир, 1972. — 184 с.
- История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени.
- История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. II: Математика XVII столетия.
- История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1972. — Т. III: Математика XVIII столетия.
- Энциклопедия элементарной математики. Книга первая. Арифметика / под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М.—Л.: Государственное издательство технико-теоретической литературы, 1951. — 448 с.
- Avigad, Jeremy. Number theory and elementary arithmetic // Philosophia Mathematica. — 2003. — Vol. 11. — № 3. — P. 257—284. (инг.)
- Boyer C. B., Merzbach U. C. A History of Mathematics. — John Wiley & Sons, 2010. — 640 p. (инг.)



























![{\displaystyle a^{n \over m}={\sqrt[{m}]{a^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85badcf829bab2418d4a469945119ab2dbf27f89)









































































