Сикһеҙлек
| Сикһеҙлек | |
 | |
| Тамғалау | ∞[d] |
|---|---|
| Вики-проект | Проект:Математика[d] |
| Ҡапма-ҡаршыһы | 0[1] һәм бесконечно малое[d] |

Сикһеҙлек — сиктәрен билдәләү йәки һан миҡдарын күрһәтеү мөмкин булмаған, сикһеҙ, иге-сиге булмаған, бөткөһөҙ предметтарҙы һәм күренештәрҙе ҡылыҡһырлау өсөн ҡулланылған фекерләү категорияһы[2]. Сикле, иҫәпләнә торған, сиге булған тигәнгә ҡапма-ҡаршы ҡулланыла. Математикала[⇨], логикала[⇨] һәм философияла[⇨] даими тикшерелә, шулай уҡ психологияла, теологияла, физикала[⇨] шуға ярашлы рәүештә сикһеҙлекте аңлау, статусы һәм тәбиғәте тураһында мәсьәләләр өйрәнелә.
Тарихи сикһеҙлектең беренсе проблемалары — арауыҡ һәм ваҡыттың сиклелек мәсьәләләре, донъяла әйберҙәр һаны, ҡатмарлыраҡ проблемалар — континуумды сикһеҙ бүлеү мөмкинлеге[⇨], сикһеҙ объекттар менән эш итеү мөмкинлеге (актуаль сикһеҙлек проблемаһы [⇨]), сикһеҙ бәләкәй дәүмәлдәрҙең — инфинитезималдәрҙең[⇨] тәбиғәте һәм үҙҙәрен тотошо, төрлө төрҙәге сикһеҙлектәрҙең булыуы һәм улар араһындағы нисбәт[2]. Математик күмәклектәр теорияһында сикһеҙлекте тәрәнерәк тикшеренә башлайҙар [⇨], унда бер нисә сикһеҙ объекттарҙың төрлө төрҙәрен үлсәү системалары төҙөлә, ләкин өҫтәлмә яһалма сикләүҙәрһеҙ бындай төҙөүҙәр күп һандағы парадокстар[⇨] тыуҙыра, уларҙы еңеп сығыу юлдары, теоретик-күмәклекле төҙөүҙәрҙең, уларҙың нәтижәләренең һәм альтернативаларының статусы хәҙерге заман философтарының тикшеренеүҙәренең төп йүнәлештәре булып тора [⇨].

Төп төшөнсәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]Потенциаль һәм актуаль сикһеҙлек
[үҙгәртергә | сығанаҡты үҙгәртеү]Сикһеҙлек ниндәйҙер процестың сикләнмәгәнлеге итеп ҡаралырға мөмкин, мәҫәлән, Евклидтың икенсе постулатында теләһә ниндәй тура һыҙыҡты сикһеҙ һәм өҙлөкһөҙ дауам итеү мөмкинлеге раҫланғанда, процесты өҙлөкһөҙ дауам итергә мөмкин булыуы күҙ уңында тотола, ләкин ундай сикһеҙ тура һыҙыҡ кеүек үҙ аллы объекттың булыуы унан килеп сыҡмай. Шундай төрҙәге процестарҙы һәм уларҙы тасуирлаусы объекттар йыйылмаһын, потенциаль сикһеҙлек тип ҡылыҡһырлайҙар (Схоластикала «синкатегорематик сикһеҙлек» термины ҡулланыла), сикһеҙ сикһеҙ предметтарҙы һәм күренештәрҙе күҙ уңында тотмай, сикһеҙ процестың һәр фазаһында тик сикле субъекттар ғына ҡарала, йәғни ул тик сиклене өлөшләтә генә инҡар итеү булып тора[2].
Альтернативаһы булып актуаль сикһеҙлек (схоластикала — «категорематик сикһеҙлек») төшөнсәһе тора, ул сикле иҫәпләп булмаған объекттарҙы бирелгән, реаль булған, әммә бүленмәҫ һәм бер бөтөн, уларға таянып эш итергә мөмкин тип иҫәпләүҙе аңлата.[2]. Был юҫыҡта сикһеҙлек актуаль — сиклене туранан-тура һәм тулыһынса инҡар итеү булараҡ — мистиктар тарафынан төрлө дини категорияларҙы ҡылыҡһырлау өсөн ҡулланыла, хәҙерге заман математиктары актуаль сикһеҙ күмәклектәр[⇨] һәм актуаль сикһеҙ үлсәмле арауыҡтар[⇨] менән эш итәләр. Фәлсәфәлә, теологияла, логикала, математикала, тәбиғи фәндә фактик сикһеҙлектең рөхсәт ителгәнлеге һәм йөкмәткеһе тураһындағы фекерҙәр мәсьәләне ҡараған бөтә ваҡыт дауамында һиҙелерлек үҙгәрә үҙгәрә.
Сифат һәм һан яғынан сикһеҙлек
[үҙгәртергә | сығанаҡты үҙгәртеү]Сифат яғынан сикһеҙлек — объекттар һәм күренештәр бәйләнешенең дөйөм, бөтмәҫ, универсаль тәбиғәтен билдәләүсе категория[3], Абсолют, Космос, Алла, Аҡыл һәм башҡа категориялар төрлө фәлсәфәүи мәктәптәрҙә төрлө ваҡыттарҙа сифат яғынан сикһеҙлек тип ҡаралалар.
Һан яғынан сикһеҙлек сикле дәүмәлдәр менән үлсәү мөмкин булмаған процестарҙы һәм объекттарҙы ҡылыҡһырлай. Математиктар, мәҫәлән, сикһеҙ рәттәрҙең үҙсәнлектәрен, сикһеҙ үлсәмле арауыҡтарҙы, сикһеҙ һандағы элементтары булған күмәклектәрҙе өйрәнгәндә һан яғынан сикһеҙлек төшөнсәһе менән эш итәләр; логикала һәм философияла һан яғынан сикһеҙлек төшөнсәһе менән эш итеү мөмкинлектәре һәм сикләүҙәр өйрәнелә.
Континуум
[үҙгәртергә | сығанаҡты үҙгәртеү]Континуум (лат. continuum) — объекттарҙың компонент өлөштәргә сикһеҙ бүленеү мөмкинлеге һәм был процестың потенциаль сикһеҙлеге мәғәнәһендә өҙлөкһөҙлөк, бөтөнлөк идеяһына ҡараған сикһеҙлек формаһы. Континуаллек дискретлыҡҡа, өҙөклөккә, бүленмәҫ (атомар) компоненттарының булыуына ҡапма-ҡаршы ҡуйыла. Һанлы күсәрҙең киҫектәре (континуум күмәклектәр теорияһында), ниндәйҙер мәғәнәлә һанлы күсәрҙең киҫектәре менән оҡшаш, сикләнгән һәм айырып алынмалы арауыҡтарҙың билдәле бер төрө (топологияла континуум) континуумды кәүҙәләндерә. Континуумдың сикһеҙ бүленеүсәнлек үҙсәнлектәрен өйрәнеү нигеҙендә математикала өҙлөкһөҙлөк төшөнсәһе индерелә. Континуумдың онтологик тәбиғәте, тәбиғәт фәнендә континуумдың статус тураһында мәсьәләләр антиклыҡ замандарынан башлап философтарҙың бик күп хеҙмәттәрендә сағылыш таба[4].
Инфинитезималь
[үҙгәртергә | сығанаҡты үҙгәртеү]Инфинитезималдәр — дәүмәлдәренең эҙмә-эҙлекле кәмеүе менән ҡылыҡһырланған потенциаль сикһеҙ процестарҙа, атап әйткәндә, континуумды компонент өлөштәргә бүлгәндә, кәмеүсе һанлы эҙмә-эҙлелектәрҙә, ҡайһы берҙә Ғаләмдең йә аңдың атом төҙөлөшө тураһында тәғлимәттә ҡатнашҡан сикһеҙ бәләкәй дәүмәлдәр. Исаак Ньютон һәм Готфрид Лейбниц тарафынан сикһеҙ бәләкәйҙәр иҫәпләмәһендә [⇨] булдырылған инфинитезималдәрҙең математик тасуирламаһы математик анализдың нигеҙе булып тора[5].
Математикала
[үҙгәртергә | сығанаҡты үҙгәртеү]Һандар теорияһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Сикһеҙлек тураһындағы иртә фекерҙәрҙең төп сығанаҡтарының береһе булып натураль һандар һәм натураль рәттең потенциаль сикһеҙлеге тора. Сикһеҙлек тураһында һандар теорияһында күп булмаған һөҙөмтәләрҙең береһе тип Евклидтың "Башланғыстар"ында ябай һандар күмәклегенең сикһеҙлеген киреһенән сығып иҫбатлау иҫәпләнә[6]: әгәр ябай һандар күмәклеге сикле тип уйлағанда, берәмек һәм был күмәклектәге бөтә ябай һандарҙың ҡабатландығы суммаһына тигеҙ булған һан был һандарҙың береһенә лә бүленмәй, ләкин ул саҡта был һан йә үҙе ябай һан булып тора, йәки баштағы күмәклеккә инмәгән ниндәйҙер ябай һанға бүленә; ләкин быларҙың икеһе лә баштағы шарттарға ҡаршы килә. Сикһеҙлек тураһында теоретик-һанлы фекер йөрөтөү Галилей парадоксын тыуҙыра: һәр һанға уның квадраты ярашлы ҡуйылырға мөмкин, йәғни, квадраттар бөтә һандарҙан кәм түгел, шуның менән бергә һәр һандан квадрат тамыр алып булмай, йәғни, квадраттар — бөтә һандар күмәклегенең бер өлөшө генә[7].
Һандар теорияһында актуаль сикһеҙлектең ниндәй ҙә булһа абстракцияһын ҡулланыу талап ителмәй, шулай булыуға ҡарамаҫтан, уның күп мәсьәләләре сикһеҙлек шарты формулировкаһы менән бәйле, мәҫәлән, Ҡалып:2019 йылға ҡарата, бирелгән һан модулдәре буйынса алынма тамыр булып торған ябай һандар күмәклегенең сикһеҙлеге (Артин гипотезаһы), ябай игеҙәк-һандар күмәклегенең сикһеҙлеге, һәр йоп һан өсөн айырмалары был һанға тигеҙ булған күрше ябай һандар парҙары күмәклегенең сикһеҙлеге (Полиньяк гипотезаһы), камил һандар күмәклегенең сикһеҙлеге тураһында мәсьәләләр асыҡ проблемалар булып торалар.
Сикһеҙ рәттәр
[үҙгәртергә | сығанаҡты үҙгәртеү]
Сикһеҙ рәтте ҡулланыуҙың беренсе дәлиле Архимедтың "Парабола квадратураһы"нда күренә, унда тура һыҙыҡ һәм парабола араһындығы сегменттың һәм уның менән нигеҙе шул уҡ һәм бейеклеге тигеҙ булған өсмөйөштөң майҙандарының сағыштырмаһы 4:3 тигән раҫлауҙы иҫбатлау өсөн ул сикһеҙ рәттең суммаһын иҫәпләп сығара:
- ,
һәм аҙаҡ һөҙөмтәне киреһенән сығып иҫбатлау ысулы менән киренән тикшерә[8].
1340-сы йылдарҙа Суайнсхед беренсе тапҡыр ябай кәмей барыусы геометрик прогрессия булмаған сикһеҙ рәттең суммаһын таба:
- .
Шулай уҡ XIV быуатта Орем сикһеҙ рәттәр менән эшләй, асыҡ геометрик иҫбатлауҙар ҡулланып, ул ярайһы уҡ һирәк һанлы рәттәрҙең суммаһын таб, сикһеҙ геометрик прогрессия суммаһының формулаһын (иҫбатламайынса) таба һәм гармоник рәттең таралыусанлығын иҫбатлай[8].
XVI быуатта, Оремдың һөҙөмтәләрен ҡулланып, Томаш[de] ҡатмарлы закондар менән төҙөлгән ҡайһы-бер сикһеҙ прогрессияларҙың суммаһын таба[8]. Һиндостанда XV быуатта тригонометрик функцияларҙың сикһеҙ дәрәжәле рәттәргә тарҡалмаһы табыла[8], Сангамаграманан Мадхава иң күп өлөш индерә[9].
Менголи 1650 йылда баҫылып сыҡҡан трактатында рәттәрҙең күп кенә мөһим үҙсәнлектәрен асыҡлай, рәт ҡалдығы төшөнсәһе индерә, шулай итеп аңғармаҫтан рәттәрҙе бөтөн объекттар итеп ҡарай, шулай уҡ дөйөмләштерелгән гармоник рәттең таралыусанлығын иҫбатлай[10]. Меркатор 1668 йылда логарифмик функцияның дәрәжәле рәткә тарҡалмаһын[11], ә 1667 йылда Грегори — тригонометрик функцияларҙың тарҡалмаһын аса, һәм, аҙаҡ килеп, Тейлор, Меркаторҙың, Грегориҙың, шулай уҡ Ньютондың һөҙөмтәләрен дөйөмләштереп, 1715 йылда теләһә ниндәй аналитик функцияны бирелгән нөктәлә сикһеҙ рәткә тарҡатырға мөмкин булыуын күрһәтә, шуның менән функцияларҙың киң класының ҡиммәттәрен сикһеҙ сумма итеп күрһәтеү мөмкинлеген асыҡлай.
Сикһеҙ бәләкәйҙәр иҫәпләмәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Антиклыҡ осоронан билдәле булған файҙаланып бөтөү ысулы, һәм Кавальери тарафынан 1635 йылда формулировкаланған бүленмәүселәр ысулы ниндәйҙер кимәлдә сикһеҙ бәләкәй дәүмәлдәр мәғлүмәтен ҡулланһалар ҙа, тәү башлап Валлис, Барроу һәм Грегори XVII быуат уртаһында сикһеҙ бәләкәйҙәр менән ғәмәлдәрҙе алгебралаштырырға тырышып ҡарайҙар, асыҡтан-асыҡ инфинитезималдарҙы 1680-се йылдарҙа бер үк ваҡытта Ньютон үҙенең "флюксий ысулы"нда (сикһеҙ бәләкәй үҫештәр) һәм Лейбниц (дифференциалды билдәләүсе) математик абстракциялайҙар[5].
Сикһеҙ бәләкәйҙәрҙең ҡәтғи билдәләмәһен сикләнмә, йыйылыусанлыҡ һәм өҙлөкһөҙлөк төшөнсәләрен ҡулланып XIX быуатта Коши һәм Вейерштрасс бирә, был билдәләмәләрҙә -формулировка[en] иң традицион булып китә (мәҫәлән, әгәр теләһә ниндәй өсөн, -тың шартын ҡәнәғәтләндергән теләһә ниндәй ҡиммәтендә үтәлгән табылһа, Коши буйынса функцияһының нөктәһендә сикләнмәһе тип иҫәпләнә). Сикһеҙ бәләкәйҙәрҙһең һуңыраҡ бирелгән билдәләмәләрендә тирә-яҡ — асыҡ аҫкүмәклек (Гейне) техникаһы ҡулланыла, улар тәбиғи рәүештә дөйөм топологияла (асыҡ күмәклек төшөнсәһен абстракциялаусы) дөйөмләштерелә.
Робинсондың Стандарт булмаған анализында (1960-сы йылдар) сикһеҙ бәләкәйҙәр теләһә ниндәй өсөн -ҙән ҙур булмаған дөйөмләштерелгән һандар төрө һымаҡ индереләләр, бөтә бындай һандар класы «нуль монадаһы» менән актуалләштерелә[12].
Математик анализ
[үҙгәртергә | сығанаҡты үҙгәртеү]Сикһеҙ бәләкәйҙәр иҫәпләмәһе[⇨] нигеҙендә төҙөлгән математик анализда асыҡтан-асыҡ сикһеҙ ҙур дәүмәлдәр абстракцияһы индерелә: ысын һандар күмәклегенә сикһеҙ йыраҡ нөктәләр символы һәм өҫтәлә (сик ҡиммәттәрҙе һәм йыйылыусанлыҡты билдәләү өсөн ҡулланылған киңәйтелгән һанлы тура һыҙыҡ ) төҙөлә. Символдар менән ғәмәлдәр башҡарырға мөмкин (бында — ысын һан):
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
әммә ҡайһы бер сикләүҙәр менән: билдәһеҙлек ситуациялары тыуғанда
сикһеҙлек барлыҡҡа килеүгә килтергән иң һуңғы аңлатма йөкмәткеһен асыҡлау принцибы буйынса аныҡһыҙлыҡтарҙы асыу ҡағиҙәләре ҡулланыла (мәҫәлән, Лопиталь ҡағиҙәһе), йәғни, анализда был мәғәнәлә сикке аңлатмаларҙы яҙыу өсөн дәйәмләштерелгән ҡыҫҡартыу итеп символдары ҡулланыла, ләкин тулы ҡиммәтле объект булараҡ түгел (ҡайһы бер дидактик материалдарҙа ысын һандар менән тәртип бәйләнеше менән бәйләнмәгән бер сикһеҙ йыраҡ нөктә ҡулланыла[13]).
Робинсондыңа стандарт булмаған анализында сикһеҙ бәләкәй һәм сикһеҙ ҙур дәүмәлдәр теоретик-моделле сараларҙы йәлеп итеү менән актуалләшәләр, шуның менән бергә, шул арҡала стандарт булмаған анализда мәғәнәле саралар һәм иҫбатлау ысулдары күп осраҡтарҙа классик ысулдарҙан отошло, һәм классик анализда ла табылырға мөмкин булған, ләкин күргәҙмәлек етешмәгәнлектән күренмәгән күп кенә яңы һөҙөмтәләр алынған[14].
Проектив геометрия
[үҙгәртергә | сығанаҡты үҙгәртеү]
Математикала сикһеҙлек тураһында фекерҙе актуалләштереүҙә Понселе 1822 йылда төҙөгән проектив геометрия мөһим роль уйнай, уның төп идеяларының береһе — сикһеҙ алыҫты «идеаль нөктәләргә» һәм «идеаль тура һыҙыҡтарға» проекциялағанда боролоу. Шулай, Евклид арауығында сикһеҙ яҫылыҡты проектив яҫылыҡҡа әйләндереү өсөн, параллель тура һыҙыҡтарҙың һәр класы өсөн идеаль нөктә өҫтәргә кәрәк, һәм бөтә ошондай идеаль нөктәләр (һәм тик шулар) идеаль тура һыҙыҡҡа[en] боролалар. Был төҙөүҙәрҙә ысын проектив тура һыҙыҡ һанлы тура һыҙыҡтың идеаль нөктә менән киңәйеүе () булып тора.
Шулай уҡ, анализдағы[⇨] кеүек, алынған сикһеҙлек менән проектив геометрияла ғәмәлдәр башҡарырға мөмкин (проектив геометрияла, анализдан айырмалы рәүештә, сикһеҙлектең тамғаһы юҡ, ):
- ,
- ,
- ,
- ,
- ,
- ,
шул уҡ ваҡытта аңлатмаларының мәғәнәһе юҡ.
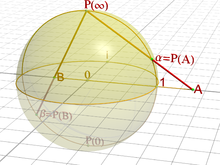
Комплекслы һанға геометрик интерпретация биргәндә, Риман1851 йылда проектив геометрия ысулдарын ҡуллана, һәм комплекслы яҫылығы өсөн проектив арауығын — һанлы проектив тура һыҙыҡтың комплекслы дөйөмләштереүен төҙөй, ул Риман сфераһы булараҡ билдәле: сфераның полюстары — һәм нөктәләре, ә стереографик проекцияһы ( нөктәһе тишеп алынған) уны комплекслы яҫылыҡҡа күсерә. Сикһеҙлек тамға менән ҡулланылған ысын анализдан айырмалы рәүештә, комплекслы анализда сикһеҙлектең тап проектив формаһы ()ҡулланыла.
Күмәклектәр теорияһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Математикала сикһеҙлек тураһында фекергә төп өлөштө күмәклектәр теорияһы индерә: актуаль сикһеҙлек һәм сикһеҙлектең төрлө төрҙәре идеяһы был теорияның ҙур өлөшөн биләй.
Сикһеҙлектең төрлө төрҙәрен үлсәү өсөн күмәклектәр теорияһында ҡеүәт (кардиналь һан) төшөнсәһе индерелә, ул сикле күмәклектәр өсөн элементтар һаны менән тап килә, ә сикһеҙ күмәклектәр өсөн биекция принцибы эшләй башлай: әгәр күмәклектәр араһында үҙ-ара-бер мәғәнәле ярашлылыҡ урынлаштырып булһа, улар тигеҙ ҡеүәтле. Шулай, натураль һандар күмәклеге бөтөн һандар күмәклеге (), йоп натураль һандар күмәклеге, бөтә рациональ һандар күмәклеге () менән тигеҙ ҡеүәтле булып сыға, ә ( һанлы тура һыҙыҡ киҫеге, континуум[⇨]) бөтә һанлы тура һыҙыҡ (), шулай уҡ -үлсәмле Евклид арауығы () менән биектив ярашлылыҡта булып сыға. Натураль һандар күмәклегенең һәм уның менән тигеҙ ҡеүәтле күмәклектәрҙең (иҫәпләү күмәклектәренең) ҡеүәте [⇨] тип, ә континуумдың ҡеүәте — тип тамғалана. Артабан, натураль һандарҙың бөтә аҫкүмәклектәре күмәклеге () һәм континуум араһында үҙ-ара-бер мәғәнәле ярашлылыҡ бар икәне асыҡлана, шулай итеп, , һәм иҫәпләү күмәклеге — бөтә сикһеҙ күмәклектәрҙән ҡеүәте буйынса иң бәләкәйе. Континуум-гипотезаға ярашлы, һәм араһында ике аралағы ҡеүәт юҡ (), шулай уҡ, Коэн 1962 йылда күрһәткәнсә, континуум-гипотезаны ла, уның кире ҡағыуын да төп күмәклектәр теорияһы аксиоматикаһында иҫбатлап булмай. Дөйөмләштерелгән континуум-гипотеза бөтә кардиналь һандар бәйләнешенә буйһоналар тип фаразлай, икенсе төрлө әйткәндә, бөтә мөмкин булған сикһеҙ кардиналь һандар нәҡ натураль һандар күмәклегенән эҙмә-эҙ булеанды (бөтә аҫкүмклектәре күмәклеге) алыу ҡеүәттәрен кәүҙәләндерәләр: [15].

Күмәклектәр теорияһы индергән сикһеҙлектең икенсе төрө — тәртип һандары (ординалдар), улар менән бәйле трансфинитлы индукция принцибы менән бер рәттән, математиктар, логиктар һәм философтар араһында ҙур бәхәс тыуҙыралар. Әгәр кардиналь һандар үҙ-ара-бер мәғәнәле ярашлылыҡҡа ҡарата эквивалентлыҡ класын ҡылыҡһырлаһалар, тәртип һаны тулыһынса тәртипкә килтерелгән күмәклектәр өҫтөнән тулы тәртип бәйләнешен һаҡлаусы биектив ярашлылыҡтарға ҡарата эквивалентлыҡ класы характеристикаһы булараҡ барлыҡҡа килә. Сикле күмәклектәр өсөн ординал һәм кардинал тап килә, әммә сикһеҙ күмәклектәр өсөн был һәр саҡ улай булмай, бер тәртип һанындағы бөтә күмәклектәр тигеҙ ҡеүәтле, ә кире раҫлау дөйөм осраҡта дөрөҫ түгел. Ординалдар натураль рәтте сикһеҙлектән ситтә эҙмә-эҙ дауам итергә мөмкин булырлыҡ итеп төҙөлә[16]:
- ,
- ,
- …
- ,
бынан һуң, бөтә сикле тәртип һандары күмәклеген итеп ҡарап, тәртипкә килтерелгән күмәклектәрҙе ҡушыу (эҙмә-эҙлекле рәүештә беренсе ҡушылыусы, һуңынан икенсе ҡушылыусы күмәклек элементтары буйынса айырым берекмәләр өҫтөнән тәртип индереп) һәм ҡабатлау (тулыһынса тәртипкә килтерелгән күмәклектәрҙең декарт ҡабатландығы өҫтөнөн лексикографик тәртип ҡулланып) операциялары базаһында тәртип һандары арифметикаһы индерелә, һәм процесс башлана:
- ,
- ,
- …
- ,
- ,
- …
Артабан , артабан — төҙөлә, ары — -һандар:
- .
Бөтә иҫәпләү ординалдар күмәклегенең (бөтә һәм ) ҡеүәте иҫәпләү күмәклектәр ҡеүәте -дән һуң килгән -гә тигеҙ булыуы иҫбатланған, артабан юғарыраҡ тәртиптәге ординалдар төҙөлә. Трансфинитлы индукция — дөйөмләштерелгән математик индукция принцибы, тәртип һандары идеяларын ҡулланып, теләһә нидәй тулыһынса тәртипкә килтерелгән күмәклеккә ҡарата раҫлауҙарҙы иҫбат итергә мөмкинлек бирә. Бурали-Форти парадоксы бөтә тәртип һандары күмәклеге ҡапма-ҡаршылыҡлы булыуын күрһәтә, ләкин күмәклектәр теорияһының күп аксиомалаштырыуында ундай күмәклектәрҙе төҙөү тыйылған.
Сикһеҙ үлсәмле арауыҡтар
[үҙгәртергә | сығанаҡты үҙгәртеү]Был мәҡәләнең өлөшө әлегә яҙылмаған. |
Фракталь геометрия
[үҙгәртергә | сығанаҡты үҙгәртеү]
Был мәҡәләнең өлөшө әлегә яҙылмаған. |
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ https://www.google.com/books/edition/Essays_on_the_Foundations_of_Mathematics/bwLSTW9uZMoC?hl=en&gbpv=1&d&pg=PA163&printsec=frontcover
- ↑ 2,0 2,1 2,2 2,3 НФЭ, 2010
- ↑ Бесконечность в философии / И. С. Алексеев // Бари — Браслет. — М. : Советская энциклопедия, 1970. — (Большая советская энциклопедия : [в 30 т.]; vol. 1969—1978, вып. 3).
- ↑ Катасонов В. Н. Непрерывность и прерывистость // Новая философская энциклопедия. — 2-е изд., испр. и дополн.. — М.: Мысль, 2010. — Т. 2. — 2816 с. — 5000 экз. — ISBN 978-5-244-01115-9.
- ↑ 5,0 5,1 Гордон, Кусраев, Кутателадзе, 2011, с. 10—13
- ↑ Книга IX, утверждение 20
- ↑ Бурбаки, 1963, с. 39
- ↑ 8,0 8,1 8,2 8,3 Паплаускас А. Б. Доньютоновский период развития бесконечных рядов. I (рус.) // Юшкевич А. П. (отв. редактор) Историко-математические исследования. — М.: Наука, 1973. — Т. XVIII. — С. 104—131.
- ↑ Dani S. G. Ancient Indian Mathematics – A Conspectus // Resonance. — 2012. — Т. 17. — № 3. — С. 236—246.
- ↑ Паплаускас А. Б. Доньютоновский период развития бесконечных рядов. II. Пьетро Менголи (рус.) // Юшкевич А. П. (отв. редактор) Историко-математические исследования. — М.: Наука, 1974. — Т. XIX. — С. 143—157.
- ↑ Паплаускас А. Б. Доньютоновский период развития бесконечных рядов. III (рус.) // Юшкевич А. П. (отв. редактор) Историко-математические исследования. — М.: Наука, 1975. — Т. XX. — С. 257—281.
- ↑ Гордон, Кусраев, Кутателадзе, 2011, с. 26
- ↑ Кудрявцев Л. Д. Краткий курс математического анализа. — 3-е изд. перераб.. — М.: Физматлит, 2005. — Т. 1. — С. 19. — 400 с. — ISBN 5-9221-0184-6.
- ↑ [{{{ссылка}}} Сикһеҙлек] — Математической энциклопедии. Драгалин А. Г. С помощью Н. а. был обнаружен ряд новых фактов. Многие классич. доказательства заметно выигрывают в наглядности при изложении их методами нестандартного анализа
- ↑ Иногда для бесконечных кардинальных чисел, представляющих мощность последовательного взятия булеанов от счётного множества используют бет-нотацию (от второй буквы еврейского алфавита — бет), в этих обозначениях обобщённая континуум-гипотеза формулируется как
- ↑ Такую схему определения предложил фон Нейман в 1920-е годы, Кантор изначально использовал другой способ
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]- Н. Бурбаки. Основания математики. Логика. Теория множеств // Очерки по истории математики / И. Г. Башмакова (перевод с французского). — М: Издательство иностранной литературы, 1963. — С. 37—53. — 292 с. — (Элементы математики).
- Виленкин Н. Я. В поисках бесконечности. — М.: Наука, 1983.
- Гордон Е. И., Кусраев А. Г., Кутателадзе С. С. Инфинитезимальный анализ: избранные темы. — М.: Наука, 2011. — 398 с. — ISBN 978-5-02-036137-9.
- Грасиан, Энрике. Открытие без границ. Бесконечность в математике. — М.: Де Агостини, 2014. — 144 с. — (Мир математики: в 45 томах, том 18). — ISBN 978-5-9774-0713-7.
- Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики = Routes et dédales / Перевод с французского А. А. Брядинской под редакцией И. Г. Башмаковой. — М.: Мир, 1986. — С. 394—402. — 432 с. — (Современная математика. Популярная серия). — 50 000 экз.
- Бесконечность / Катасонов В. Н. // «Банкетная кампания» 1904 — Большой Иргиз. — М. : Большая российская энциклопедия, 2005. — С. 413—415. — (Большая российская энциклопедия : [в 35 т.]; vol. 2004—2017, вып. 3). — ISBN 5-85270-331-1.
- Катасонов В. Н. Бесконечное // Новая философская энциклопедия / Ин-т философии РАН; Нац. обществ.-науч. фонд; Предс. научно-ред. совета В. С. Стёпин, заместители предс.: А. А. Гусейнов, Г. Ю. Семигин, уч. секр. А. П. Огурцов. — 2-е изд., испр. и допол.. — М.: Мысль, 2010. — ISBN 978-5-244-01115-9.
- Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — 446 с.



















































![{\displaystyle \mathbb {I} =[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dde877d72cff66b34f632b167b4f526ffd01e1c1)
























