Икеле иҫәпләү системаһы

Икеле иҫәпләү системаһы
Алдағы	унарная система счисления[d]
Тәртип буйынса һуңыраҡ килеүсе	троичная система счисления[d]
Основание системы счисления	2
Вики-проект	Проект:Математика[d]
Икеле иҫәпләү системаһы Викимилектә

Икеле иҫәпләү системаһы — нигеҙе 2 булған позицион иҫәпләү системаһы. Цифрлы электрон схемаларҙа логик вентилдәрҙә туранан-тура тормошҡа ашырыу арҡаһында, икеле система бөтә хәҙерге заман компьютерҙарында һәм башҡа иҫәпләү электрон ҡоролмаларҙа ҡулланыла.

Һандарҙы икеле яҙыу

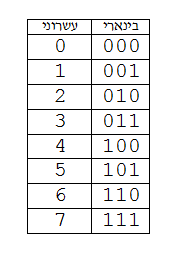
Икеле иҫәпләү системаһында һандар ике символ (0 һәм 1) ярҙамында яҙылалар. Һан ниндәй иҫәпләү системаһында яҙылған икәнен бутамаҫ өсөн, уға уң яҡта аҫтан күрһәткес ҡуялар. Мәҫәлән, һан унарлы системала 5₁₀, икеле системала 101₂. Ҡайһы берҙә икеле һанды 0b префиксы йәки & (амперсанд) символы менән тамғалайҙар, мәҫәлән 0b101 йәки ярашлы рәүештә &101.

Икеле иҫәпләү системаһында (унарлынан башҡа икенсе иҫәпләү системаһындағы кеүек) тамғалар берәрләп уҡыла. Мәҫәлән, 101₂ һаны «бер ноль бер» тип әйтелә.

Натураль һандар

Икеле иҫәпләү системаһында $(a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}$ тип яҙылған натураль һандың ҡиммәте:

$(a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}=\sum _{k=0}^{n-1}a_{k}2^{k},$

бында:

• $n$ — һандағы цифрҙар (тамғалар) һаны,
• $a_{k}$ — {0,1} күмәклегенән цифрҙар,
• $k$ — цифрҙың тәртип номеры.

Тиҫкәре һандар

Тиҫкәре икеле һандар унарлы һандар кеүек үк тамғаланалар: һан алдында «−» тамғаһы. Йәғни, икеле иҫәпләү системаһында яҙылған $(-a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}$ тиҫкәре бөтөн һанының ҡиммәте:

$(-a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}=-\sum _{k=0}^{n-1}a_{k}2^{k}.$

Иҫәпләү техникаһында тиҫкәре икеле һандарҙы өҫтәлмә кодта яҙыу ҡулланыла.

Кәсер һандар

Икеле иҫәпләү системаһында $(a_{n-1}a_{n-2}\dots a_{1}a_{0},a_{-1}a_{-2}\dots a_{-(m-1)}a_{-m})_{2}$ тип яҙылған кәсер һандың ҡиммәте:

$(a_{n-1}a_{n-2}\dots a_{1}a_{0},a_{-1}a_{-2}\dots a_{-(m-1)}a_{-m})_{2}=\sum _{k=-m}^{n-1}a_{k}2^{k},$

бында:

• $m$ — һандың кәсер өлөшөнөң цифрҙар һаны,
• $a_{k}$ — $\{0,1\}$ күмәклегенән цифрҙар.

Икеле һандарҙы ҡушыу, алыу һәм ҡабатлау

Ҡушыу таблицаһы

+	0	1
0	0	1
1	1	10( күмәклегенән цифрҙарразрядҡа күсереү)

Алыу таблицаһы

-	0	1
0	0	1
1	(өлкән разрядтан бурысҡа алыу) 1	0

«Бағаналап» ҡушыуға миҫал (14₁₀ + 5₁₀ = 19₁₀ йәки 1110₂ + 101₂ = 10011₂):

+		1	1	1	0
			1	0	1
	1	0	0	1	1

Ҡабатлау таблицаһы

×	0	1
0	0	0
1	0	1

«Бағаналап» ҡабатлауға миҫал (14₁₀ * 5₁₀ = 70₁₀ йәки 1110₂ * 101₂ = 1000110₂):

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

Һандарҙы үҙгәртеү

Икеле иҫәпләү системаһынан унарлы иҫәпләү системаһына үҙгәртеү өсөн түбәндәге 2 нигеҙенең дәрәжәләре таблицаһын ҡулланалар:

1024

512

256

128

64

32

16

8

4

2

1

1 цифрынан башлап бөтә цифрҙар икегә ҡабатлана. 1-ҙән һуң торған нөктә икеле нөктә тип атала.

Икеле һандарҙы унарлыға үҙгәртеү

110001₂ икеле һаны бирелһен, ти. Унарлыға үҙгәртеү өсөн уны разрядтары буйынса сумма рәүешендә түбәндәгесә күрһәтегеҙ:

1 * 2⁵ + 1 * 2⁴ + 0 * 2³ + 0 * 2² + 0 * 2¹ + 1 * 2⁰ = 49

Шул уҡ бер аҙ икенсерәк:

1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49

Быны түбәндәгесә таблица рәүешендә яҙырға була:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	0	1
				+32	+16	+0	+0	+0	+1

Уңдан һулға хәрәкәт итегеҙ. Һәр икеле берәмек аҫтында аҫҡы юлда уның эквивалентын яҙығыҙ. Килеп сыҡҡан унарлы һандарҙы ҡушығыҙ. Шулай итеп, 110001₂ икеле һаны 49₁₀ унарлы һанына тиң.

Кәсерле икеле һандарҙы унарлыға үҙгәртеү

1011010,101₂ һанын унарлыға үҙгәртергә кәрәк. Был һанды түбәндәгесә яҙабыҙ:

1 * 2⁶ + 0 * 2⁵ + 1 * 2⁴ + 1 * 2³ + 0 * 2² + 1 * 2¹ + 0 * 2⁰ + 1 * 2⁻¹ + 0 * 2⁻² + 1 * 2⁻³ = 90,625

Шул уҡ бер аҙ икенсерәк:

1 * 64 + 0 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 0 * 1 + 1 * 0,5 + 0 * 0,25 + 1 * 0,125 = 90,625

Йәки таблица буйынса:

64	32	16	8	4	2	1		0.5	0.25	0.125
1	0	1	1	0	1	0	,	1	0	1
+64	+0	+16	+8	+0	+2	+0		+0.5	+0	+0.125

Горнер ысулы менән үҙгәртеү

Һандарҙы икеленән унарлы системаға был ысул менән үҙгәртеү өсөн, цифрҙарҙы, алдан табылған һөҙөмтәне системаның нигеҙенә (был осраҡта 2) ҡабатлап, һулдан уңға ҡушырға кәрәк. Горнер ысулы менән ғәҙәттә икеленән унарлы системаға күсерәләр. Кире операция ҡатмарлы, сөнки икеле иҫәпләү системаһында ҡушыу һәм ҡабатлау күнекмәһе талап ителә.

Мәҫәлән, 1011011₂ икеле һаны унарлы системаға ошолай күсерелә:

0*2 + 1 = 1
1*2 + 0 = 2
2*2 + 1 = 5
5*2 + 1 = 11
11*2 + 0 = 22
22*2 + 1 = 45
45*2 + 1 = 91

Йәғни унарлы системала был һан 91 тип яҙыла.

Горнер ысулы менән һандарҙың кәсер өлөшөн күсереү

Цифрҙар һандан уңдан һулға ҡарай алыналар һәм иҫәпләү системаһының нигеҙенә (2) бүленәләр.

Мәҫәлән 0,1101₂

(0 + 1)/2 = 0,5
(0,5 + 0)/2 = 0,25
(0,25 + 1)/2 = 0,625
(0,625 + 1)/2 = 0,8125

Яуап: 0,1101₂= 0,8125₁₀

Унарлы һандарҙы икелегә үҙгәртеү

19 һанын икелегә үҙгәртергә кәрәк икән, ти. Түбәндәге процедура менән файҙаланырға мөмкин:

19/2 = 9 с остатком 1
9/2 = 4 c остатком 1
4/2 = 2 без остатка 0
2/2 = 1 без остатка 0
1/2 = 0 с остатком 1

Шулай итеп, беҙ һәр бүлендекте мы делим каждое частное на 2-гә бүләбеҙ һәм ҡалдыҡты икеле яҙыуҙың аҙағына яҙабыҙ. Бүлеүҙе ҡалдыҡ 0 булғанға тиклем дауам итәбеҙ. Һөҙөмтә уңдан һулға ҡарай яҙыла. Йәғни түбәндәге (1) цифры иң һулдағы була һәм башҡа шулай. Һөҙөмтәлә 19 һанын икеле яҙыуҙа табабыҙ: 10011.

Унарлы кәсер һандарҙы икеле һандарға үҙгәртеү

Әгәр бирелгән һандың бөтөн өлөшө булһа, ул кәсер өлөшөнән айырым үҙгәртелә. Кәсер һанды унарлы иҫәпләү системаһынан икелегә күсереү түбәндәге алгоритм буйынса тормошҡа ашырыла:

• Кәсер икеле иҫәпләү системаһының нигеҙенә (2) ҡабатлана;
• Килеп сыҡҡан ҡабатландыҡтың бөтөн өлөшө икеле иҫәпләү системаһындағы һандың өлкән разряды сифатында айырып алына;
• Әгәр килеп сыҡҡан ҡабатландыҡтың кәсер өлөшө нулгә тигеҙ булһа, йәки талап ителгән теүәллеккә өлгәшелһә, алгоритм тамамлана. Кире осраҡта ҡабатландыҡтың кәсер өәлөшө өҫтөндә иҫәпләүҙәр дауам итә.

Миҫал: 206,116 унарлы һанын икелегә күсерергә кәрәк икән, ти.

Алдан һүрәтләнгән алгоритм буйынса бөтөн өлөшөн үҙгәртеү 206₁₀=11001110₂ һөҙөмтәһен бирә. Дробную часть 0,116 кәсер өлөшөн 2 нигеҙенә ҡабатлайбыҙ, ҡабатландыҡтың бөтөн өлөшөн эҙләнгән икеле кәсер һандың өтөрҙән һуңғы разрядына яҙып барабыҙ:

0,116 • 2 = 0,232
0,232 • 2 = 0,464
0,464 • 2 = 0,928
0,928 • 2 = 1,856
0,856 • 2 = 1,712
0,712 • 2 = 1,424
0,424 • 2 = 0,848
0,848 • 2 = 1,696
0,696 • 2 = 1,392
0,392 • 2 = 0,784
и т. д.

Шулай итеп 0,116₁₀ ≈ 0,0001110110₂

Табабыҙ: 206,116₁₀ ≈ 11001110,0001110110₂

Ҡулланылышы

Цифрлы ҡоролмаларҙа

Икеле система цифрлы ҡоролмаларҙа ҡулланыла, сөнки иң ябай система булып тора һәм түбәндәге талаптарға тап килә:

• Чем меньше значений существует в Системала ни тиклем әҙ ҡиммәттәр булһа, шул тиклем был ҡиммәттәр менән эш итеүсе айырым элементтарҙы әҙерләү ябайыраҡ. Айырып әйткәндә, икеле иҫәпләү системаһының ике цифры бик күп физик күренештәр менән күрһәтелергә мөмкин: ток бар (ток сик ҡиммәтенән ҙурыраҡ) — ток юҡ (ток сик ҡиммәтенән кәмерәк), магнит ҡырының индукцияһы сик ҡиммәтенән ҙурыраҡ йәки юҡ (магнит ҡырының индукцияһы сик ҡиммәтенән бәләкәйерәк) һәм башҡа шулай.
• Элемент торошоноң һаны ни тиклем әҙ булһа, шул тиклем тотҡарлыҡ тотороҡлолоғо ҙурыраҡ һәм ул шәберәк эшләй аласаҡ. Мәҫәлән, өс торошто көсөргәнеш, ток йәки магнит ҡырының индукцияһы дәүмәле аша кодлау өсөн, ике сик ҡиммәте һәм тотҡарлыҡ тотороҡлолоғона һәм мәғлүмәт һаҡлау ышаныслылығына булышлыҡ итеүсе ике компаратор индерергә кәрәк.
• Икеле арифметика ябайыраҡ. Һандар өҫтөндә төп ғәмәлдәр — ҡушыу һәм ҡабатлау таблицалары ябай.

Цифрлы электроникала икеле иҫәпләү системаһында бер икеле разрядҡа икелерегистрҙың бер икеле разряды ярашлы, йәғни ике торошло (0,1) икеле триггер.

Иҫәпләү техникаһында тиҫкәре икеле һандарҙы өҫтәлмә кодта яҙыу киң ҡулланыла. Мәҫәлән, −5₁₀ һаны −101₂ тип яҙылырға мөмкин, ләкин 32-битлы компьютерҙа 11111111111111111111111111111011₂ тип һаҡланасаҡ.

Инглиз үлсәү системаһында

Һыҙыҡлы үлсәмдәрҙе дюймдарҙа күрһәткәндә традиция буйынса унарлы түгел, ә икеле кәсерҙәр ҡулланыла, мәҫәлән: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ һәм башҡа шулай.

Дөйөмләштереү

Икеле иҫәпләү системаһы икеле кодлау системаһы һәм нигеҙе 2 булған күрһәткесле ауырлыҡ функцияһы комбинацияһы булып тора. Әйтергә кәрәк, һан икеле кодта яҙылырға мөмкин, ә был ваҡытта иҫәпләү системаһы икеле түгел, ә икенсе нигеҙ менән булырға мөмкин. Миҫал: икеле-унарлы кодлау, унда унарлы цифрҙар икеле күренештә яҙыла, ә иҫәпләү системаһы — унарлы.

Тарихы

• 8 триграмманан һәм 64 гексаграмманан тулы йыйылма, 3-битлы һәм 6-битлы цифрҙар аналогы, боронғо Ҡытайҙа Книга Перемендағы классик текстарҙа билдәле була. Книга Переменда ярашлы икеле цифрҙар (0-дән 63-кә тиклем) ҡиммәттәре менән тура килтереп урынлашҡан гексаграммалар тәртибе һәм уларҙы табыу ысулы Ҡытай ғалимы һәм философы Шао Юн тарафынан XI быуатта эшләнгән. Әммә Шао Юн, ике символлы кортеждарҙы лексикографик тәртиптә урынлаштырғанда, икеле арифметика ҡағиҙәләрен аңлауын дәлилләүсе иҫбатлауҙар юҡ.

• Һинд математигы Пингала (б. э. тиклем 200 йыл) икеле иҫәпләү системаһын беренсе билдәле ҡулланып, поэзияны һүрәтләү өсөн математик нигеҙҙәрен эшләй.

• Үҙәк Андтарҙа (Перу, Боливия) дәүләт һәм йәмғиәт маҡсатында б. э. тиклем I—II мең йыллыҡта киң ҡулланылған мәғлүмәт базаһының прообразы булып Инктарҙың төйөнлө яҙыуы — кипу тора, ул унарлы системаның һанлы яҙыуҙарынан, шулай уҡ кодлауҙың икеле системаһында һанлы булмаған яҙыуҙарҙан тора. Кипуҙа беренсел һәм өҫтәлмә асҡыстар, позицион һандар, төҫ менән кодлау һәм ҡабатланыусы мәғлүмәттәрҙең серияларын төҙөү ҡулланыла. Кипу кешелек тарихында беренсе тапҡыр бухгалтер иҫәбен алып барыуҙың икеләтә яҙыу кеүек ысулын ҡулланыу өсөн файҙаланылған.

• Икеле цифрҙар комбинацияһы булған йыйылмалар африкалылар тарафынан, урта быуат геомантияһы менән бер рәттән, традицион күрәҙәлек итеүҙәрҙә (Ифа кеүек) ҡулланылған.

• 1605 йылда Френсис Бэкон алфавитының хәрефтәрен икеле цифрҙар эҙмә-эҙлелектәренә ҡайтарып ҡалдырырға мөмкин булған системаны һүрәтләй, улар үҙ сиратында теләһә ниндәй осраҡлы текстарҙа шрифттарҙың саҡ ҡына һиҙелерлек үҙгәреше кеүек кодланырға мөмкиндәр. Икеле кодлауҙың дөйөм теорияһы үҫешендә, был ысул теләһә ниндәй объекттарға ҡулланылырға мөмкин, тигән иҫкәртеү мөһим аҙым булып тора (cм. Шифр Бэкона).

• Хәҙерге икеле система Лейбниц тарафынан XVII быуатта Explication de l’Arithmétique Binaire исемле хеҙмәтендә тулыһынса һүрәтләнгән. Лейбниц иҫәпләү системаһында, хәҙерге икеле системаһындағы кеүек, 0 һәм 1 цифрҙары ҡулланылған. Ҡытай мәҙәниәте менән мауығыусы кеше булараҡ, Лейбниц Книга Перемен тураһында белгән һәм гексаграммалар 0-дән 111111-гә тиклемге икеле һандарға тап килеүен билдәләгән. Ул, был сағылдырыу Ҡытайҙың шул замандың фәлсәфәүи математикаһында ҙур ҡаҙаныштарын раҫлаусы дәлил булып тороуы менән һоҡланған.

• 1854 йылда инглиз математигы Джордж Буль алгебраик системаларҙы логикаға ҡулланылышта һүрәтләүсе хеҙмәтен баҫтырып сығара, ул хәҙерге ваҡытта Булева алгебра йәки логика алгебраһы булараҡ билдәле. Уның логик иҫәпләмәһенә хәҙерге заман цифрлы электрон схемалар эшләүҙә мөһим роль үтәргә насип була.

• 1937 йылда Клод Шеннон MITта Символический анализ релейных и переключательных схем исемле кандидатлыҡ диссертацияһын яҡлауға тәҡдим итә, унда булева алгебра һәм икеле арифметика электрон реле һәм күсереп ялғағыстарға ҡарата ҡулланылған. Бөтә хәҙерге заман цифрлы техника асылда Шеннондың диссертацияһына нигеҙләнгән.

• 1937 йылдың ноябрендә, аҙаҡ Bell Labsта эшләүсе Джордж Штибиц, реле базаһында «Model K» компьютерын (инглиз теленән «Kitchen», йыйыу башҡарылған кухня) яһай, ул икеле ҡушыуҙы башҡара. 1938 йыл аҙағында Bell Labs Штибиц етәкселегендә тикшеренеү программаһын йәйелдерә. Уның етәкселегендә эшләнгән, 1940 йылдың 8 ғинуарында әҙер булған компьютер комплекслы һандар менән ғәмәлдәр башҡара белә. Дартмут колледжында American Mathematical Society конференцияһында демонстрациялау ваҡытында, 1940 йылдың 11 сентябрендә, Штибиц алыҫтағы комплекслы һандар калькуляторына телефон линияһы буйынса телетайп ҡулланып командалар ебәреү мөмкинлеген демонстрациялай. Был алыҫтағы иҫәпләү машинаһын телефон линияһы ярҙамында ҡулланырға беренсе маташыу була. Демонстрациялау шаһиты булған конференцияла ҡатнашыусылар араһында Джон фон Нейман, Джон Мокли һәм Норберт Винер була, аҙаҡ улар был турала үҙҙәренең мемуарҙарында яҙалар.

Ҡыҙыҡлы факттар

• Новосибирск Академҡаласығында Рәсәй фәндәр академияһы Себер бүлексәһенең иҫәпләү технологиялары институты (элекке СССР фәндәр академияһы Себер бүлексәһенең Иҫәпләү Үҙәге) бинаһының фронтонында 70₁₀-ға тигеҙ булған 1000110 икеле һан бар, ул бинаны төҙөү датаһын символлаштыра (1970 йыл).

Шулай уҡ ҡарағыҙ

• Битовые операции
• Иҫәпләү системалары
• Бит
• Байт
• Единицы измерения информации
• Двоичные логические элементы
• Двоичный триггер
• Двоично-десятичный код
• Двоичное кодирование
• Азбука Морзе

Һылтанмалар

• Бинарное счисление // Брокгауз һәм Ефрондың энциклопедик һүҙлеге: 86 томда (82 т. һәм 4 өҫтәмә том). — СПб., 1890—1907. (рус.)
• Учебное пособие «Арифметические основы ЭВМ и систем». Часть 1. Системы счисления
• Hexadecimal Decimal Binary Octal Converter for programmers 2011 йыл 21 февраль архивланған.
• Конвертер целых и дробных чисел из двоичной системы счисления в десятичную.
• Фомин С. В. Системы счисления. — М.: Наука, 1987. — 48 с. — (Популярные лекции по математике). (альтернативная ссылка), (альтернативная ссылка на сайт РГБ)
• Системы счисления : методические указания и задание к самостоятельной работе по дисциплине "Информатика" для студентов всех специальностей. — Саратов: Саратовский гос. технический ун-т, 2009. — 24 с.
• Любомудров А.А. Системы счисления. Методы перевода чисел из позиционной системы счисления с основанием p1 в позиционную систему счисления с основанием p2. — М.: НИЯУ МИФИ, 2009. — 28 с.
• Андреева Е. В. Системы счисления и компьютерная арифметика : учеб. пособие. — изд. 3-е. — М.: Бином. Лаб. знаний, 2004. — 254 с.
• YouTube сайтында Системы счисления (16 сент. 2014 г.)
• YouTube сайтында МГИУ : Информатика. Выпуск 1. Системы счисления. (21 февр. 2014 г.)