Симметрия
Был мәҡәлә башҡорт Википедияһының һайланған мәҡәләләре исемлегенә керә. |
| Симметрия | |
 | |
| Һештег | Symmetry һәм Symmetrie |
|---|---|
| Ҡапма-ҡаршыһы | асимметрия[d] |

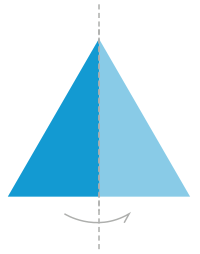

Симме́три́я (бор. грек. συμμετρία = «нисбәтлелек»; συμ- «бергә» + μετρέω «үлсәйем»), киң мәғәнәлә — ниндәйҙер үҙгәрештәрҙә, әүерелештәрҙә (мәҫәлән: тороштоң, энергияның, мәғлүмәттең, башҡаның) асылған ярашлылыҡ, үҙгәрмәүсәнлек (инвариантлылыҡ). Шулай, мәҫәлән, есемдең сферик симметрияһы, әгәр уны арауыҡта ирекле мөйөштәргә борһаң (бер нөктәһен урынында һаҡлап), есемдең күренеше үҙгәрмәй тигәнде аңлата. Ике яҡлы симметрия ниндәйҙер яҫылыҡҡа ҡарата уң һәм һул яғы бер төрлө күренә тигәнде аңлата.
Симметрияның боҙолоуы йәки булмауы асимметрия йәки аритмия тип атала[1].
Дөйөм симметрия үҙенсәлектәре төркөмдәр теорияһы ярҙамында тасуирлана.
Симметрия теүәл йәки яҡынса булырға мөмкин.
Геометрияла симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]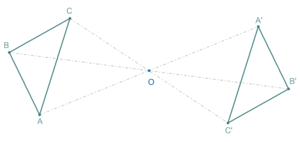
Геометрик симметрия — симметрияның күптәргә билдәле төрө. Геометрик объект, әгәр геометрик әүерелештән һуң уның ҡайһы бер тәүге үҙенсәлектәре һаҡланып ҡалһа, симметриялы тип атала. Мәҫәлән, үҙәге тирәләй боролған түңәрәк баштағы түңәрәктеке кеүек үк формаға һәм ҙурлыҡҡа эйә. Шуға күрә түңәрәк боролошҡа ҡарата симметриялы була (йәғни уның күсәр симметрияһы бар). Геометрик объект өсөн мөмкин булған симметрия төрҙәре мөмкин булған бик күп геометрик әүерелеүҙәргә һәм әүерелдерелгәндән һуң объекттың ниндәй үҙенсәлектәре үҙгәрешһеҙ ҡалырға тейеш булыуына бәйле.
Геометрик симметрия төрҙәре:
- Көҙгөләгесә симметрия
- Күсәрле симметрия
- Әйләнмә симметрия
- Үҙәкле симметрия
- Шыумалы симметрия
- Бормалы симметрия
Көҙгөләгесә симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Көҙгөләгесә симметрия йәки сағылыш — хәрәкәтһеҙ нөктәләр күмәклеге гиперяҫылыҡ булған (өс үлсәмле арауыҡ осрағында — яҫылыҡ ҡына) Евклид арауығы хәрәкәте. Көҙгөләгесә симметрия термины объекттарҙың ярашлы симметрия тибын тасуирлау өсөн дә, йәғни объект сағылыш операцияһы ваҡытында үҙ-үҙенә күскәндә ҡулланыла. Был математика төшөнсәһе оптикала объекттарҙың һәм уларҙың яҫы көҙгөлә сағылған (уйҙырма) һүрәттәренең нисбәттәрен тасуирлай. Күп кенә тәбиғәт закондарында (кристаллографияла, химияла, физикала, биологияла һәм башҡаларҙа, шулай уҡ сәнғәттә һәм сәнғәт фәнендә) сағылыш таба.
Күсәр симметрияһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Әгәр фигураның һәр нөктәһе өсөн А тура һыҙығына ҡарата симметриялы нөктә шулай уҡ был фигураға ҡараһа, фигура А тура һыҙығына ҡарата симметриялы тип атала.
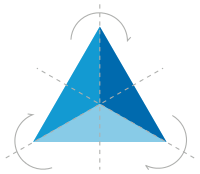
Әйләнмә симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Әйләнмә симметрия — объекттың m-үлсәмле Евклид арауығының бөтә йәки бер нисә үҙ боролошона ҡарата симметрияһын аңлатҡан термин. Үҙ боролоштары тип йүнәлеште һаҡлаусы изометрия төрҙәре атала. Шулай итеп, боролоштарға яуап биргән симметрия төркөмдәре — E+(m) (ҡара: Евклид төркөмө) төркөмөнөң аҫтөркөмө ул.
Трансляцион симметрия әйләнмә симметрияның айырым осрағы — сикһеҙ алыҫта ятҡан нөктә тирәләй боролош — итеп ҡаралырға мөмкин. Ошолай дөйөмләштергәндә әйләнмә симметрия төркөмө тулы E+(m) менән тап килә. Бындай төрҙәге симметрия сикле һандағы объекттарға ҡулланылмай, сөнки бөтә арауыҡты бер төрлө яһай, әммә ул физик законлылыҡтарҙы төҙөгәндә файҙаланыла.
Арауыҡтың тотороҡло нөктәһе тирәләй үҙ боролоштары күмәклеге махсус ортогональ төркөм SO(m) — билдәләүсеһе 1-гә тигеҙ булған m×m ортогональ матрицалар төркөмөн — төҙөй. m = 3 булған айырым осраҡ өсөн төркөм боролоштар төркөмө тигән махсус исем йөрөтә.
Физикала боролоштар төркөмөнә ҡарата инвариантлыҡ арауыҡтың изотроплығы тип атала (арауыҡта бөтә йүнәлештәр тиң хоҡуҡлы) һәм физик закондарҙың, атап әйткәндә, боролошҡа ҡағылышлы хәрәкәт тигеҙләмәләренең инвариантлығында сағыла. Нётер теоремаһы был инвариантлыҡты һаҡланыусы дәүмәл (хәрәкәт интегралы) — мөйөш моменты — булыуы менән бәйләй.

Нөктәгә ҡарата симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]A нөктәһенә ҡарата үҙәк симметрия (ҡайһы берҙә үҙәк инверсия) тип X нөктәһен A нөктәһе XX киҫегенең уртаһы булырлыҡ итеп X нөктәһенә күсергән арауыҡты әүерелдереү атала. Үҙәге A нөктәһендә булған үҙәкле симметрия ғәҙәттә тип тамғалана, сөнки тамғаланышын күсәр симметрияһы менән бутарға мөмкин. Әгәр фигураның теләһә ниндәй нөктәһе өсөн A нөктәһенә ҡарата уға симметриялы нөктә шулай уҡ был фигураға инһә, был фигура A нөктәһенә ҡарата симметриялы тип атала. A нөктәһе фигураның симметрия үҙәге тип атала. Шулай уҡ фигура үҙәкле симметрияға эйә тип тә әйтәләр. Был үҙгәртеүҙең икенсе исеме — үҙәге A булған симметрия. Планиметрияла үҙәкле симметрия боролоштоң айырым осрағы, дөрөҫөрәге, 180 градусҡа боролош булып тора.
Шыумалы симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Шыумалы симметрия — Евклид яҫылығының изометрияһы. Шыумалы симметрия тип ниндәйҙер тура һыҙығына ҡарата симметрия һәм -ға параллель векторға (был вектор нулле вектор булырға ла мөмкин) күсерелеш композицияһы атала. Шыумалы симметрияны 3 күсәр симметрияһы композицияһы рәүешендә күрһәтергә мөмкин (Шаль теоремаһы).
Симметрия физикала
[үҙгәртергә | сығанаҡты үҙгәртеү]Теоретик физикала физик системаның торошо ҡайһы бер тигеҙләмәләр менән һүрәтләнә. Әгәр был тигеҙләмәләр берәй төрлө симметрияға эйә булһа, йыш ҡына уларҙы сисеүҙе һаҡланыусы дәүмәлдәрҙе (хәрәкәт интегралдарын) табыу юлы менән ябайлаштырып була. Шулай, классик механикала өҙлөкһөҙ симметрияның һәр төрөнә һаҡланыусы дәүмәлде ҡаршы ҡуйыусы Нётер теоремаһы сығарыла. Уға ярашлы, мәҫәлән, есемдең хәрәкәт тигеҙләмәһенең инвариантлығы ваҡыт үтеү менән — энергия һаҡланыу законына; арауыҡта күсеүгә ҡарата инвариантлыҡ — импульс һаҡланыу законына; боролошҡа ҡарата инвариантлыҡ импульс моменты һаҡланыу законына килтерә.
Суперсимметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Суперсимметрия йәки Ферми — Бозе симметрияһы — тәбиғәттә бозон һәм фермиондарҙы бәйләп тороусы гипотетик симметрия. Абстракт суперсимметрия әүерелеше фермионлы һәм бозонлы квант ҡырҙарын бергә бәйләй, шуға күрә улар бер-береһенә әүерелергә мөмкин. Образлы итеп әйткәндә, суперсимметрия матдәне тәьҫирләшеүгә (йәки нурланышҡа) әүерелдерергә мөмкин, һәм киреһенсә.
2009 йыл башына ҡарата суперсимметрия эксперимент ярҙамында дөрөҫләнмәгән физик фараз булып тора. Теүәл симметрия мәғәнәһендә беҙҙең донъяның суперсимметриялы булмауы аныҡ асыҡланған, сөнки теләһә ниндәй суперсимметриялы моделдә суперсимметриялы әүерелеү менән бәйле бозондар һәм фермиондар бер үк массаға, зарядҡа һәм башҡа квант һандарына (спиндан тыш) эйә булырға тейеш. Был талап тәбиғәттә билдәле булған киҫәксәләр өсөн үтәлмәй. Шуға ҡарамаҫтан, шундай энергетик лимит бар: уларҙы уҙғанда ҡырҙар суперсимметриялы әүерелеүҙәргә буйһона, ә лимит сиктәрендә — юҡ тип фараз ителә. Бындай осраҡта ғәҙәти өлөшсәләрҙең суперпартнерҙары булған өлөшсәләр ғәҙәти өлөшсәләр менән сағыштырғанда бик ауыр булалар. Ғәҙәти өлөшсәләрҙең суперпартнерҙарын эҙләү — хәҙерге заман юғары энергиялар физикаһының төп бурыстарының береһе. Оло адронлы коллайдер[2], әгәр улар булһа, суперсимметрик киҫәксәләрҙе асыр һәм өйрәнә алыр, йәки, әгәр бер нәмә лә табып булмаһа, суперсимметрик теорияны ҙур шик аҫтына ҡуйыр тип көтөлә.
Трансляцион симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Трансляцион симметрия — ҡаралған системаның үҙенсәлектәре трансляция векторы тип аталған билдәле бер векторға күсештә үҙгәрмәгән симметрия төрө. Мәҫәлән, бер төрлө мөхит теләһә ниндәй векторға күскәндә лә үҙенә-үҙе тап килә, шуға күрә уға трансляцион симметрия хас.
Трансляцион симметрия шулай уҡ кристалдарға ла хас. Был осраҡта трансляция векторҙары, уларҙың һаны сикһеҙ булһа ла, ирекле түгел. Кристаллик рәшәткәнең бөтә трансляция векторҙары араһынан шулай итеп 3 һыҙыҡлы бойондороҡһоҙ вектор һайларға мөмкин, был саҡта трансляцияның теләһә ниндәй башҡа векторы был векторҙарҙың бөтөн-һыҙыҡлы комбинацияһы булыр ине. Был өс вектор кристалл рәшәткәһенең базисын тәшкил итә.
Төркөмдәр теорияһы күрһәтеүенсә, кристалдарҙа трансляцион симметрия θ=2π/n мөйөштәренә боролоштар менән генә яраша, бында n 1, 2, 3, 4, 6 ҡиммәттәрен ҡабул итергә мөмкин.
180, 120, 90, 60 градуслы мөйөштәргә боролош ваҡытында кристалдарҙа атомдарҙың торошо үҙгәрмәй. Кристалдарҙың n-сы тәртиптәге боролош күсәре бар, тиҙәр.
Яҫы дүрт үлсәмле арауыҡ-ваҡытҡа күсереү физик закондарҙы үҙгәртмәй. Ҡырҙар теорияһында трансляцион симметриялар, Нётер теоремаһына ярашлы, энергия-импульс тензоры һаҡланыуға тура килә. Атап әйткәндә, тик ваҡыт трансляциялары — энергия һаҡланыу законына тура килә, ә тик арауыҡтағы күсештәр импульс һаҡланыу законына тура килә.
Биологияла симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]
Биологияла симметрия — был есемдең оҡшаш (бер төрлө, үлсәме буйынса тигеҙ) өлөшсәләренең йәки тере организм формаһының, тере организм йыйылмаһының симметрия үҙәгенә йәки күсәренә ҡарата законға ярашлы урынлашыуы. Симметрия төрө тән төҙөлөшөн билдәләп кенә ҡалмай, ә хайуандың ағзалары системаһының үҫеү мөмкинлектәрен билдәләй. Күп кенә күп күҙәнәкле организмдарҙың төҙөлөшө симметрияның билдәле бер формаларын сағылдыра. Хайуандың кәүҙәһен уйҙа ғына икегә, уң һәм һул яртыға, бүлеп ҡарағанда, симметрияның бындай формаһын билатераль тип атайҙар. Симметрияның был төрө күпселек төрҙәргә, шулай уҡ кешеләргә хас. Уйҙа ғына хайуандың тәнен бер түгел, ә бер нисә симметрия яҫылыҡтары менән тигеҙ өлөштәргә бүлеп ҡарағанда, бындай хайуанды радиаль симметриялы тип атайҙар. Симметрияның был төрө һирәк осрай.
Асимметрия — симметрияның булмауы. Ҡайһы берҙә был терминды тәү сиратта симметриянан мәхрүм ителгән организмдарҙы йәки уның айырым элементтарын тасуирлау өсөн, диссимметрияға — симметрияны икенсел юғалтыуға ҡапма-ҡаршы ҡулланалар.
Симметрия һәм асимметрия — кире төшөнсәләр. Организмдар ни тиклем симметриялы булһа, ул шул тиклем әҙерәк асимметриялы һәм киреһенсә. Ррганизмдарҙың бик аҙы ғына тулыһынса асимметриялы. Шуның менән бергә форма үҙгәртеүсәнлекте (мәҫәлән, амебаның) симметрия юҡлыҡтан айыра белергә кәрәк. Тәбиғәттә һәм, атап әйткәндә, тере тәбиғәттә симметрия абсолют түгел һәм унда һәр ваҡыт бер ни тиклем дәрәжәлә асимметрия була. Мәҫәлән, үҫемлектәрҙең симметриялы япрағы уртаға бөкләгәндә теүәл генә тап килмәй.
Биологик объекттарҙа симметрияның түбәндәге төрҙәре осрай:
- сферик симметрия — өс үлсәмле арауыҡта ирекле мөйөштәргә боролошҡа ҡарата симметриялылыҡ.
- аксиаль симметрия (радиаль симметрия, билдәһеҙ тәртиптәге боролош симметрияһы) — ниндәйҙер күсәр тирәләй ирекле мөйөштәргә боролошҡа ҡарата симметриялылыҡ.
- n-сы тәртиптәге боролош симметрияһы — ниндәйҙер күсәр тирәләй 360°/n мөйөштәренә боролошҡа ҡарата симметрия.
- ике яҡлы (билатераль) симметрия — симметрия яҫылығына ҡарата симметриялылыҡ (көҙгөләгесә сағылыш симметрияһы).
- трансляцион симметрия — арауыҡтың ниндәй ҙә булһа йүнәлештә ниндәйҙер алыҫлыҡҡа күсештәренә ҡарата симметриялылыҡ (уның айырым осрағы хайуандарҙа — метамерия (биология)).
- триаксиаль симметрия — арауыҡтың бөтә өс күсәре буйынса симметрияның булмауы.
Радиаль симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Биологияла, әгәр өс үлсәмле йән эйәһе аша бер йәки бер нисә симметрия күсәре үтһә, радиаль симметрия тураһында һүҙ бара. Был ваҡытта радиаль симметриялы хайуандарҙың симметрия яҫылығы булырға ла, булмаҫҡа ла мөмкин. Шулай, Velella сифонофораһының икенсе тәртип симметрия күсәре бар һәм симметрия яҫылығы юҡ[3]
Ғәҙәттә симметрия күсәре аша ике йәки унан күберәк симметрия яҫылығы үтә. Был яҫылыҡтар тура һыҙыҡ — симметрия күсәре буйынса киҫешәләр. Әгәр хайуан был күсәр тирәләй билдәле бер градусҡа боролһа, ул саҡта ул үҙ-үҙенә сағыла (үҙе менән тап килә). Шундай бер нисә (полиаксон симметрия) йәки бер (монаксон симметрия) симметрия күсәре булырға мөмкин. Полиаксон симметрия протистар араһында киң таралған (мәҫәлән, радиолярий).
Ҡағиҙә булараҡ, күп күҙәнәкле хайуандарҙың берҙән-бер симметрия күсәренең ике осо (полюсы) тиң түгел (мәҫәлән, медузаларҙың бер полюсында (ораль) ауыҙ урынлашҡан, ә ҡапма-ҡаршы полюсында (абораль) — ҡалпаҡтың өҫкө өлөшө. Бындай симметрия (радиаль симметрия варианты) сағыштырма анатомияла бер күсәрле-гетерополь симметрия тип атала. Ике үлсәмле проекцияла, әгәр симметрия күсәре проекция яҫылығына перпендикуляр йүнәлһә, радиаль симметрия һаҡлана ала. Ябайлаштырып әйткәндә, радиаль симметрияның һаҡланыуы күҙәтеү мөйөшөнә бәйле.
Радиаль симметрия күпселек саҡҡыс күҙәнәктәре булған хайуандарға, шулай уҡ күпселек энәтирелеләргә хас. Улар араһында шулай уҡ биш симметрия яҫылығына нигеҙләнгән пентасимметрия тип аталғандар осрай. Энә тирелеләрҙә радиаль симметрия икенсел: уларҙың ҡарышлауыҡтары ике яҡлы симметриялы, ә өлкән хайуандарҙа тышҡы радиаль симметрия иләкле пластинкалары булғанлыҡтан боҙола.
Хас булған радиаль симметриянан тыш ике нур һымаҡ радиаль симметрия бар (ике симметрия яҫылығы, мәҫәлән, тараҡлыларҙа). Әгәр симметрия яҫылығы берәү генә булһа, симметрия билатераль (Bilateria төркөмө хайуандарының шундай симметрияһы бар) була.
Сәскәле үҫемлектәрҙә йыш ҡына радиаль симметрик сәскә осрай: 3 симметрия яҫылығы (баҡа һылыуҡасы), 4 симметрия яҫылығы (Potentílla récta), 5 симметрия яҫылығы (ҡыңғырау сәскә), 6 симметрия яҫылығы (көҙгө сәскә). Радиаль симметриялы сәскәләрҙе — актиноморфлы, ә билатераль симметриялы сәскәләрҙе зигоморфлы тип атап йөрөтәләр.
Билатераль симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Билатераль симметрия (ике яҡлы симметрия) — көҙгөләгесә сағылыш симметрияһы, был ваҡытта объекттың бер симметрия яҫылығы бар, уға ҡарата уның ике яртыһы көҙгөләгесә симметриялы. Әгәр симметрия яҫылығына A нөктәһенән перпендикуляр төшөрһәң һәм артабан симметрия яҫылығындағы О нөктәһенән уны AО оҙонлоғона дауам итһәң, ул бөтә яҡтан A нөктәһенә оҡшаш булған A1 нөктәһенә эләгә. Билатераль симметриялы объекттарҙың симметрия күсәре булмай. Хайуандарҙа билатераль симметрия уның кәүҙәһенең уң һәм һул яртыһының оҡшашлығында йәки тулыһынса тиерлек берҙәйлегендә сағыла. Шул уҡ ваҡытта һәр ваҡыт симметриянан осраҡлы тайпылыш була (мәҫәлән, папилляр һыҙаттарҙағы айырмалар, тамырҙың тармаҡланыуы һәм кеше миңенең уң һәм һул ҡулында төрлөсә урынлашыуы). Йыш ҡына тышҡы төҙөлөштә ҙур булмаған, ләкин ҡануни айырмалар була (мәҫәлән, ун ҡул менән эш итеүсе кешенең уң ҡулы үҫешкәнерәк мускулатуралы була), кәүҙәнең уң һәм һул яртыһында эске ағзалар урынлашыуында ла һиҙелерҙек айырма була. Мәҫәлән, һөтимәрҙәрҙәрҙең йөрәге ғәҙәттә симметриялы урынлашмай, һулға тайпылыш менән урынлаша.
Хайуандар эволюцияһында билатераль симметрияның барлыҡҡа килеүе субстрат буйлап (һыу ятҡылыҡтары төбөнән) шыуышыу менән бәйле, шуға ҡарап, кәүҙәнең арҡа һәм ҡорһаҡ яғы, уң һәм һул яртылары формалаша. Дөйөм алғанда, хайуандар араһында билатераль симметрия әүҙем хәрәкәтсән формаларҙа ултырыусандарға ҡарағанда нығыраҡ сағыла.
Билатераль симметрия, энә тирелеләрҙән башҡа, бөтә юғары үҫешкән хайуандарға хас. Тере организмдарҙың башҡа батшалыҡтарында билатераль симметрия аҙ һандағы формаларға хас. Протисталар араһында ул дипломонадалар (мәҫәлән, лямблия), трипаносомаларҙың ҡайһы бер формалары, бодонидалар, күп фораминифераларҙың ҡабырсаҡтары өсөн хас. Үҫемлектәрҙә ғәҙәттә билатераль симметрия бөтә организмға түгел, ә уның айырым өлөштәренә — япрағына һәм сәскәһенә хас. Билатераль симметрик сәскәләрҙе ботаниктар зигоморфлы тип йөрөтә.
Химияла симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Симметрия химия өсөн бик мөһим, сөнки спектроскопияла, квант химияһында һәм кристаллографияла күҙәтеүҙәрҙе аңлата.
Кристаллографик нөктәле симметрия төркөмө — ул кристалдың макросимметрияһын һүрәтләүсе нөктәле симметрия төркөмө. Кристалдарҙа бары тик 1, 2, 3, 4 һәм 6 тәртибендәге күсәрҙәр генә (боролош һәм үҙборолош булмаған) рөхсәт ителгәнлектән, сикһеҙ һандағы нөктәле симметрия төркөмөнөң тик 32-һе генә кристаллографик симметрия төркөмөнә ҡарай.
Анизотропия (бор. грек. ἄνισος — тигеҙ түгел һәм τρόπος — йүнәлеш һүҙҙәренән) — изотропияға ҡапма-ҡаршы, мөхит эсендәге төрлө йүнәлештәрҙә мөхит үҙенсәлектәрендәге (мәҫәлән, физик: һығылмалылыҡ, электр үткәреүсәнлек, йылы үткәреүсәнлек, һыныу күрһәткесе, тауыш йәки яҡтылыҡ тиҙлеге һ. б.) айырма. Кристалдарҙа анизотроплыҡтың сәбәбе булып, тәртип буйынса урынлашҡан атомдарҙың, молекулаларҙың һәм иондарҙың үҙ-ара тәьҫир итешеү көсөнөң йәки улар араһындағы алыҫлыҡтың (шулай уҡ улар менән туранан-тура бәйле булмаған ҡайһы бер дәүмәлдәрҙең, мәҫәлән, полярлашыу йәки электр үткәреүсәнлек) төрлө йүнәлештәр буйынса бер төрлө булмауы тора. Шулай уҡ молекуляр кристалдарҙың анизотропияһына уның молекулаларының асимметрияһы сәбәп булырға мөмкин. Макроскопик йәһәттән был төрлөлөк, ҡағиҙә булараҡ, әгәр кристалл структураһы артыҡ симметриялы булмаһа ғына күренә.

Диндә һәм мәҙәниәттә симметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Кешеләрҙә маҡсатты симметрияла күреү тенденцияһы симметрияның йыш ҡына донъя диндәре символдарының айырылғыһыҙ бер өлөшө булып тороуы сәбәптәренең береһе тип фараз ителә. Уңдағы һүрәттә күп миҫалдарҙың ҡайһы берҙәре генә һүрәтләнгән.
Кешеләр төрлө контекстарҙа социаль үҙ-ара тәьҫир итешеүҙең симметриялы тәбиғәтен (асимметрик балансты ла ла индергән) күҙәтә. Улар үҙ-ара мөнәсәбәт, эмпатия, ғәфү үтенеү, диалог, ихтирам итеү, ғәҙеллек һәм үс алыу баһаһын үҙ эсенә ала. Симметриялы үҙ-ара мөнәсәбәт «беҙ төрлө-төрлө» тигән сигнал ебәрә, ә асимметриялы үҙ-ара мөнәсәбәт «мин үҙенсәлекле, һинән яҡшыраҡ» тигән фекерҙе белдерә. Тиҫтерҙәр менән мөнәсәбәт симметрия нигеҙендә ҡорола, ә власть мөнәсәбәттәре — асимметрия[4] нигеҙендә.
Симметрияның башҡа төрҙәре
[үҙгәртергә | сығанаҡты үҙгәртеү]Тәбиғи фәндәрҙә һәм математикала осраған симметрия төрҙәре:
- n-сы тәртиптәге симметрия —ниндәй ҙә булһа күсәр тирәләй 360°/n мөйөштәренә боролошҡа ҡарата симметриялылыҡ. Zn төркөмө менән һүрәтләнә;
- Лоренцса инвариантлыҡ — Минковский арауыҡ-ваҡытында ирекле боролоштарға ҡарата симметриялылыҡ;
- калибрлау инвариантлығы — ҡырҙың квант теорияһында калибрлау үҙгәртеүҙәрендә калибрлау теорияһы тигеҙләмәләре күренешенең бәйһеҙлеге (атап әйткәндә, Янг—Миллс теориялары);
- юғары симметрия — төркөм анализында симметрия;
- кайносимметрия — электрон конфигурация күренеше (термин уны асҡан С А. Щукарев тарафынан индерелгән), уға бәйле икенсел периодлылыҡ (Е. В. Бирон тарафынан асылған).
- ниндәйҙер объекттың (күпҡырҙың йәки метрик арауыҡтағы нөктәләр күмәклегенең) симметриялы төркөмө ― уларға ҡарата был объект инвариант булып торған, төркөм операцияһы сифатында композиция менән, бөтә хәрәкәттәр төркөмө.
- Симметриялы төркөм — бирелгән күмәклегенең композиция ғәмәленә ҡарата бөтә алмаштырмалары [[Төркөм (математика)|төркөмө] (йәғни биекцияһы).
Асимметрия
[үҙгәртергә | сығанаҡты үҙгәртеү]Асимметрияны (бор. грек. ασυμμετρία һүҙмә-һүҙ «бер-береһенә тура килмәү» һәм μετρέω «үлсәйем» һүҙҙәренән) симметрияның теләһә ниндәй боҙолоуы тип һанарға мөмкин. Термин йыш ҡына һынлы сәнғәттә һәм визуаль объекттарға ҡарата ҡулланыла. Сәнғәт ижадында асимметрия форма биреүҙең (йәки композицияның) төп сараларының береһе сифатында сығыш яһарға мөмкин (һәм бик йыш сығыш яһай). Сәнғәттә яҡын төшөнсәләрҙең береһе — аритмия.
Организмда даими рәүештә күҙәнәктәр бүленеүе менән бәйле, асимметрия организмда, һәр хәлдә бер үлсәмдә, биологик симметрия менән бер рәттән ғәҙәти күренеш булып тора (шулай уҡ ҡарағыҙ: Ярымшарҙар араһында асимметрия). Луи Пастер, биологик молекулалар йыһан [йәғни физик] көстәре арҡаһында асимметриялы, улар, үҙҙәренекенә оҡшаш үҙенсәлектәр (асимметриялылыҡ) һалып, был молекулаларҙың формалашыуы өҫтөнән контролде тормошҡа ашыра, тип уйлай. Ул ваҡытта, хатта хәҙер ҙә, физик процестарҙа симметрияға ҙур әһәмиәт бирелә, шулай уҡ ваҡыттан башлап, фундаменталь физик асимметриялар билдәле.
«Өҫтөнлөк иткән ҡул» төшөнсәһе бар, ул кешеләрҙә һәм хайуандарҙа күнекмәләр үҫешендә асимметрияны аңлата. Нервы ептәрен бер ҡул (тәпәй) менән күнекмәләргә өйрәтеү ваҡытында күнектереү, ике ҡул менән шул уҡ күнектереүгә ҡарағанда, әҙерәк ваҡыт ала[5]
Асимметрия төшөнсәһе шулай уҡ физикала (Ғаләмдең барионлы асимметрияһы, Ом асимметрияһы, Һыйышлыҡ асимметрияһы), математикала (асимметрия коэффициенты, асимметриялы мөнәсәбәттәр, Асимметриялы атом, Асимметриялы криптография), архитектурала һәм башҡаларҙа бар.
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ Власов В.Г. Иллюстрированный художественный словарь. — СПб.: Икар, 1993. — С. 23.
- ↑ Официальный короткий технический отчёт CERN от 2 июля 2008 года(недоступная ссылка) (инг.)
- ↑ Беклемишев В. Н. Основны сравнительной анатомии беспозвоночных. (в 2-х томах). Т.1. М., «Наука», 1964.
- ↑ Emotional Competency
- ↑ Martin Gardner. The New Ambidextrous Universe: Symmetry and Asymmetry from Mirror Reflections to Superstrings. — 3. — New York: W.H.Freeman & Co Ltd., 1990. — 416 p. — ISBN 0486442446.
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]- Урманцев Ю. А. Симметрия природы и природа симметрии. — М., Мысль, 1974.
- Вигнер Е. Этюды о симметрии. — М., Мир, 1971. — 320 с.
- Нокс Р., Голд А. Симметрия в твердом теле. — М., Наука, 1970. — 424 с.
- Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. — М., Наука, 1972. — 340 с.
- Вернадский В. И. Химическое строение биосферы Земли и её окружения. — М., Наука, 1965. — 373 с.
- Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. — М., Наука, 1967. — 284 с.
- Под ред. Сенешаль М., Флека Дж. Узоры симметрии. — М., Мир, 1980. — 269 с.
- Ю. К. Егоров-Тисменко, Г. П. Литвинская Теория симметрии кристаллов, ГЕОС, 2000.
- П. М. Зоркий Симметрия молекул и кристаллических структур, МГУ, 1986.
- А. В. Шубников Симметрия и антисимметрия конечных фигур, Изд-во АН СССР, 1951
Һылтанмалар
[үҙгәртергә | сығанаҡты үҙгәртеү]- Симметрия (в биологии) — Ҙур совет энциклопедияһында мәҡәлә
- Симметрия — физик энциклопедияһында мәҡәлә.





